Note

Go to the end to download the full example code. or to run this example in your browser via Binder

在鸢尾花数据集上绘制不同的SVM分类器#

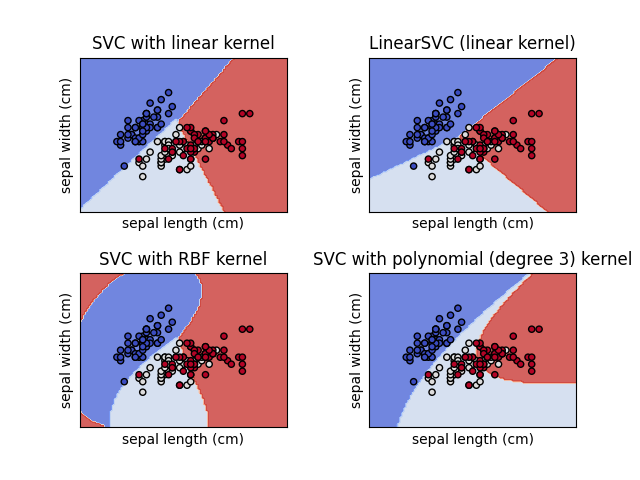
在鸢尾花数据集的二维投影上比较不同的线性SVM分类器。我们只考虑该数据集的前两个特征：

萼片长度
萼片宽度

此示例展示了如何绘制具有不同核函数的四个SVM分类器的决策面。

线性模型 LinearSVC() 和 SVC(kernel='linear') 产生的决策边界略有不同。这可能是由于以下差异：

LinearSVC 最小化平方铰链损失，而 SVC 最小化常规铰链损失。
LinearSVC 使用一对多（也称为一对其余）多类减少方法，而 SVC 使用一对一多类减少方法。

两个线性模型都有线性决策边界（相交的超平面），而非线性核模型（多项式或高斯RBF）具有更灵活的非线性决策边界，其形状取决于核的种类及其参数。

Note

虽然绘制玩具二维数据集分类器的决策函数有助于直观理解它们各自的表达能力，但请注意，这些直觉并不总是能推广到更现实的高维问题。

SVC with linear kernel, LinearSVC (linear kernel), SVC with RBF kernel, SVC with polynomial (degree 3) kernel

import matplotlib.pyplot as plt

from sklearn import datasets, svm
from sklearn.inspection import DecisionBoundaryDisplay

# 导入一些数据来玩玩
iris = datasets.load_iris()
# 取前两个特征。我们可以通过使用一个二维数据集来避免这种情况。
X = iris.data[:, :2]
y = iris.target

# 我们创建一个SVM实例并拟合我们的数据。我们不对数据进行缩放，因为我们想绘制支持向量。
C = 1.0  # SVM regularization parameter
models = (
    svm.SVC(kernel="linear", C=C),
    svm.LinearSVC(C=C, max_iter=10000),
    svm.SVC(kernel="rbf", gamma=0.7, C=C),
    svm.SVC(kernel="poly", degree=3, gamma="auto", C=C),
)
models = (clf.fit(X, y) for clf in models)

# title for the plots
titles = (
    "SVC with linear kernel",
    "LinearSVC (linear kernel)",
    "SVC with RBF kernel",
    "SVC with polynomial (degree 3) kernel",
)

# 设置2x2网格进行绘图。
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

X0, X1 = X[:, 0], X[:, 1]

for clf, title, ax in zip(models, titles, sub.flatten()):
    disp = DecisionBoundaryDisplay.from_estimator(
        clf,
        X,
        response_method="predict",
        cmap=plt.cm.coolwarm,
        alpha=0.8,
        ax=ax,
        xlabel=iris.feature_names[0],
        ylabel=iris.feature_names[1],
    )
    ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors="k")
    ax.set_xticks(())
    ax.set_yticks(())
    ax.set_title(title)

plt.show()