Note
Go to the end to download the full example code. or to run this example in your browser via Binder
缩放SVC的正则化参数#
以下示例说明了在使用:ref:svm 进行:ref:分类 <svm_classification> 时缩放正则化参数的效果。
对于SVC分类,我们关注的是以下方程的风险最小化:
其中
用于设置正则化的量
是样本和模型参数的 损失函数
是模型参数的 惩罚函数
如果我们认为损失函数是每个样本的单独误差,那么数据拟合项或每个样本误差的总和会随着我们添加更多样本而增加。然而,惩罚项不会增加。
例如,当使用:ref:交叉验证 <cross_validation> 来设置正则化参数 C 时,主问题和交叉验证折叠内的较小问题之间的样本数量会有所不同。
由于损失函数依赖于样本数量,后者会影响所选的 C 值。由此产生的问题是“我们如何优化调整C以考虑不同数量的训练样本?”
# 作者:scikit-learn 开发者
# SPDX 许可证标识符:BSD-3-Clause
数据生成#
在这个示例中,我们研究了在使用L1或L2惩罚时,重新参数化正则化参数 C 以考虑样本数量的效果。为此,我们创建了一个具有大量特征的合成数据集,其中只有少数特征是有信息量的。因此,我们期望正则化将系数缩小到接近零(L2惩罚)或精确为零(L1惩罚)。
from sklearn.datasets import make_classification
n_samples, n_features = 100, 300
X, y = make_classification(
n_samples=n_samples, n_features=n_features, n_informative=5, random_state=1
)
L1-惩罚情况#
在L1情况下,理论表明,只要有强正则化,估计器的预测能力就不如知道真实分布的模型(即使在样本量无限增长的情况下),因为它可能会将一些本来具有预测能力的特征的权重设为零,从而引入偏差。然而,理论也表明,通过调整 C ,可以找到正确的非零参数集及其符号。
我们定义一个带有L1惩罚的线性SVC。
我们通过交叉验证计算不同 C 值的平均测试得分。
import numpy as np
import pandas as pd
from sklearn.model_selection import ShuffleSplit, validation_curve
Cs = np.logspace(-2.3, -1.3, 10)
train_sizes = np.linspace(0.3, 0.7, 3)
labels = [f"fraction: {train_size}" for train_size in train_sizes]
shuffle_params = {
"test_size": 0.3,
"n_splits": 150,
"random_state": 1,
}
results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
cv = ShuffleSplit(train_size=train_size, **shuffle_params)
train_scores, test_scores = validation_curve(
model_l1,
X,
y,
param_name="C",
param_range=Cs,
cv=cv,
n_jobs=2,
)
results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))
# 绘制未缩放C的结果
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("CV score")
axes[0].set_title("No scaling")
for label in labels:
best_C = results.loc[results[label].idxmax(), "C"]
axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.7)
# 通过缩放C绘制结果
for train_size_idx, label in enumerate(labels):
train_size = train_sizes[train_size_idx]
results_scaled = results[[label]].assign(
C_scaled=Cs * float(n_samples * np.sqrt(train_size))
)
results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.7)
axes[1].set_title("Scaling C by sqrt(1 / n_samples)")
_ = fig.suptitle("Effect of scaling C with L1 penalty")
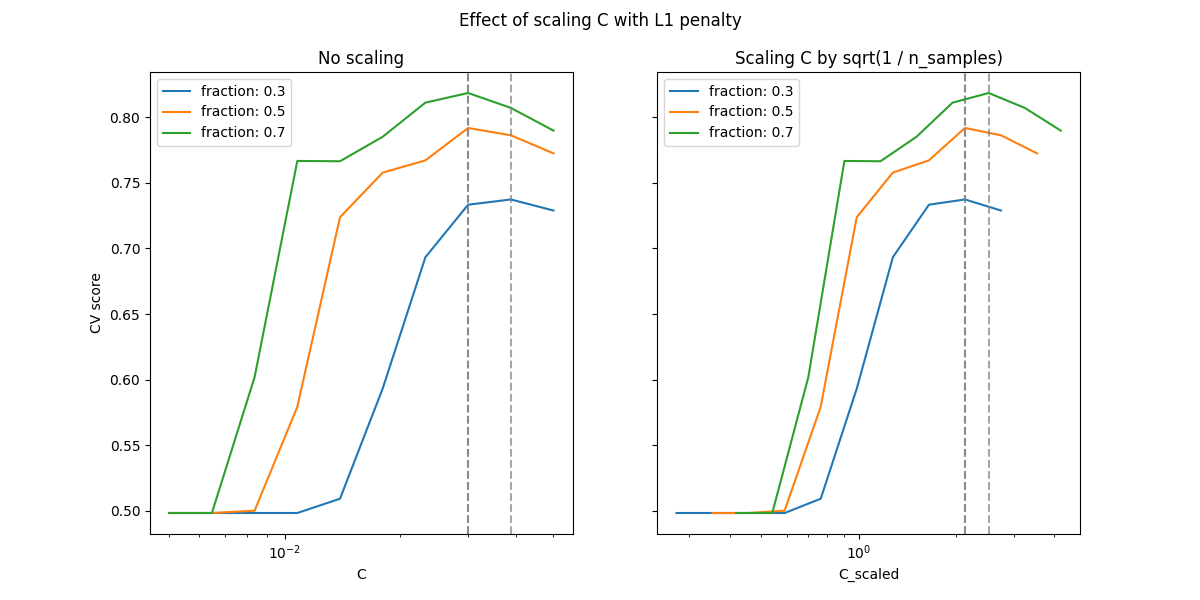
在小 C (强正则化)区域,模型学习到的所有系数都是零,导致严重欠拟合。实际上,该区域的准确率处于随机水平。
使用默认的缩放比例会得到一个相对稳定的 C 最优值,而从欠拟合区域过渡取决于训练样本的数量。重新参数化会导致结果更加稳定。
参见例如:arxiv:On the prediction performance of the Lasso <1402.1700> 的定理3或:arxiv:Simultaneous analysis of Lasso and Dantzig selector <0801.1095> ,其中正则化参数总是假定与1 / sqrt(n_samples)成正比。
L2-惩罚情况#
我们可以对L2惩罚进行类似的实验。在这种情况下,理论上为了实现预测一致性,惩罚参数应随着样本数量的增加保持不变。
model_l2 = LinearSVC(penalty="l2", loss="squared_hinge", dual=True)
Cs = np.logspace(-8, 4, 11)
labels = [f"fraction: {train_size}" for train_size in train_sizes]
results = {"C": Cs}
for label, train_size in zip(labels, train_sizes):
cv = ShuffleSplit(train_size=train_size, **shuffle_params)
train_scores, test_scores = validation_curve(
model_l2,
X,
y,
param_name="C",
param_range=Cs,
cv=cv,
n_jobs=2,
)
results[label] = test_scores.mean(axis=1)
results = pd.DataFrame(results)
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(12, 6))
# 绘制未缩放C的结果
results.plot(x="C", ax=axes[0], logx=True)
axes[0].set_ylabel("CV score")
axes[0].set_title("No scaling")
for label in labels:
best_C = results.loc[results[label].idxmax(), "C"]
axes[0].axvline(x=best_C, linestyle="--", color="grey", alpha=0.8)
# 通过缩放C绘制结果
for train_size_idx, label in enumerate(labels):
results_scaled = results[[label]].assign(
C_scaled=Cs * float(n_samples * np.sqrt(train_sizes[train_size_idx]))
)
results_scaled.plot(x="C_scaled", ax=axes[1], logx=True, label=label)
best_C_scaled = results_scaled["C_scaled"].loc[results[label].idxmax()]
axes[1].axvline(x=best_C_scaled, linestyle="--", color="grey", alpha=0.8)
axes[1].set_title("Scaling C by sqrt(1 / n_samples)")
fig.suptitle("Effect of scaling C with L2 penalty")
plt.show()
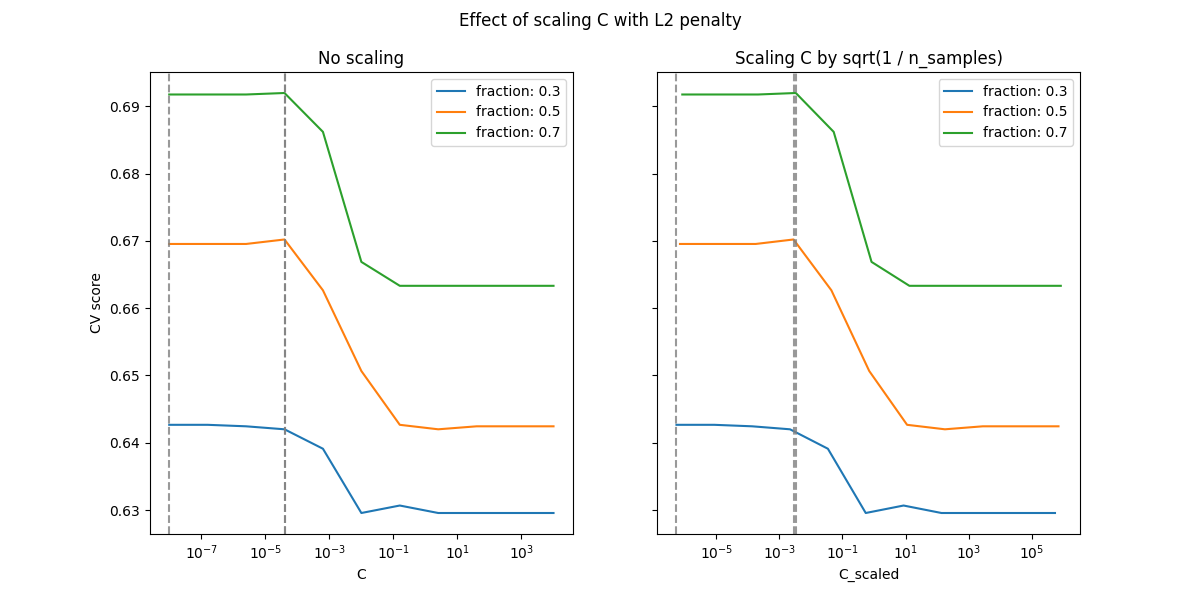
对于L2惩罚情况,重新参数化似乎对正则化的最优值稳定性影响较小。过拟合区域的过渡发生在更广泛的范围内,并且准确性似乎没有降到随机水平。
尝试将值增加到 n_splits=1_000 以在 L2 情况下获得更好的结果,这里由于文档生成器的限制未显示。
Total running time of the script: (0 minutes 8.553 seconds)
Related examples
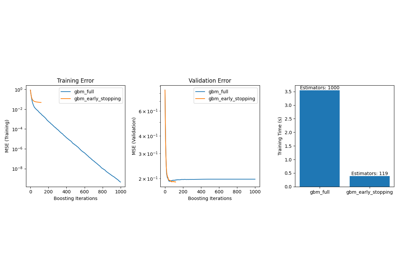
sphx_glr_auto_examples_model_selection_plot_successive_halving_iterations.py