DecisionTreeDiscretiser#
离散化包括通过创建一组连续的区间或箱,将连续变量转换为离散特征,这些区间或箱覆盖了变量值的范围。
离散化是许多数据科学项目中常见的数据预处理步骤,因为它简化了连续属性,并有可能提高模型性能或加快模型训练速度。
决策树离散化#
决策树基于连续特征的离散分区进行决策。在训练过程中,决策树评估所有可能的特征值以找到最佳分割点,即在该特征值处分割最大化信息增益,换句话说,减少不纯度。它在每个节点重复此过程,直到将所有样本分配到特定的叶节点或终端节点。因此,分类树和回归树可以自然地找到区间的最佳界限,以最大化类别一致性。
使用决策树进行离散化包括使用决策树算法来识别每个连续变量的最佳分区。在找到最佳分区后,我们将变量的值排序到这些区间中。
基于决策树的离散化是一种有监督的离散化方法,即,区间限制是基于类别或目标的一致性来确定的。简单来说,我们需要目标变量来训练决策树。
优势#
决策树返回的输出与目标呈单调相关。
树的末端节点,或称为箱子,显示了减少的熵,也就是说,每个箱子内的观测值彼此之间比与其他箱子的观测值更为相似。
限制#
可能导致过拟合
我们需要调整一些决策树参数以获得最佳的区间数量。
决策树离散化器#
The DecisionTreeDiscretiser() 应用基于决策树算法找到的区间限制的离散化。它使用决策树来找到最佳的区间限制。接下来,它将变量排序到这些区间中。
转换后的变量可以具有区间的限制作为值,一个表示值被排序到哪个区间的序数,或者可选地,决策树的预测。在任何情况下,变量的值的数量将是有限的。
理论上,决策树离散化创建了与目标具有单调关系的离散变量,因此,转换后的特征更适合训练线性模型,如线性回归或逻辑回归。
原始想法#
决策树离散化的方法基于KDD 2009竞赛的获胜解决方案:
Niculescu-Mizil 等人。“通过集成选择赢得 KDD Cup Orange 挑战”。JMLR: 研讨会和会议论文集 7: 23-34. KDD 2009.
在原文中,数据集中的每个特征都通过仅使用该特征训练有限深度的决策树(深度为2、3或4)进行重新编码,并让该树预测目标。该决策树的概率预测被用作与目标线性(或至少单调)相关的附加特征。
根据作者的说法,这些新功能的添加对线性模型的性能产生了显著影响。
代码示例#
在接下来的部分中,我们将进行决策树离散化以展示 DecisionTreeDiscretiser() 的功能。我们将使用决策树对 Ames 房价数据集中的 2 个数值变量进行离散化。
首先,我们将使用决策树的预测来转换变量,接下来,我们将返回区间限制,最后,我们将返回分箱顺序。
使用决策树的预测进行离散化#
首先我们加载数据,并将其分为训练集和测试集:
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
data = fetch_openml(name='house_prices', as_frame=True)
data = data.frame
X = data.drop(['SalePrice', 'Id'], axis=1)
y = data['SalePrice']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42)
print(X_train.head())
在以下输出中,我们看到了房价数据集的预测变量:
MSSubClass MSZoning LotFrontage LotArea Street Alley LotShape \
254 20 RL 70.0 8400 Pave NaN Reg
1066 60 RL 59.0 7837 Pave NaN IR1
638 30 RL 67.0 8777 Pave NaN Reg
799 50 RL 60.0 7200 Pave NaN Reg
380 50 RL 50.0 5000 Pave Pave Reg
LandContour Utilities LotConfig ... ScreenPorch PoolArea PoolQC Fence \
254 Lvl AllPub Inside ... 0 0 NaN NaN
1066 Lvl AllPub Inside ... 0 0 NaN NaN
638 Lvl AllPub Inside ... 0 0 NaN MnPrv
799 Lvl AllPub Corner ... 0 0 NaN MnPrv
380 Lvl AllPub Inside ... 0 0 NaN NaN
MiscFeature MiscVal MoSold YrSold SaleType SaleCondition
254 NaN 0 6 2010 WD Normal
1066 NaN 0 5 2009 WD Normal
638 NaN 0 5 2008 WD Normal
799 NaN 0 6 2007 WD Normal
380 NaN 0 5 2010 WD Normal
[5 rows x 79 columns]
我们设置了决策树离散器,以使用决策树找到最佳区间。
默认情况下,DecisionTreeDiscretiser() 将通过交叉验证优化决策树分类器或回归器的深度。这就是为什么我们需要选择适当的优化指标。在这个例子中,我们使用决策树回归,因此我们选择均方误差指标。
我们在 bin_output 中指定,我们希望用决策树的预测结果替换连续属性值。
from feature_engine.discretisation import DecisionTreeDiscretiser
disc = DecisionTreeDiscretiser(bin_output="prediction",
cv=3,
scoring='neg_mean_squared_error',
variables=['LotArea', 'GrLivArea'],
regression=True)
disc.fit(X_train, y_train)
scoring 和 cv 参数的工作方式与任何 scikit-learn 估计器的参数完全相同。因此,我们可以传递任何对这些估计器也有效的值。有关更多信息,请查看 scikit-learn 的文档。
使用 fit() 方法,转换器为每个连续特征拟合一个决策树。然后,我们可以继续用树的预测值替换变量值,并显示转换后的变量:
train_t = disc.transform(X_train)
test_t = disc.transform(X_test)
print(train_t[['LotArea', 'GrLivArea']].head())
在这种情况下,原始值被每个决策树的预测值所替代:
LotArea GrLivArea
254 144174.283688 152471.713568
1066 144174.283688 191760.966667
638 176117.741848 97156.250000
799 144174.283688 202178.409091
380 144174.283688 202178.409091
决策树做出离散预测,这就是为什么我们会在转换后的变量中看到有限数量的值:
train_t[['LotArea', 'GrLivArea']].nunique()
LotArea 4
GrLivArea 16
dtype: int64
binner_dict_ 存储了每个决策树的详细信息。
disc.binner_dict_
{'LotArea': GridSearchCV(cv=3, estimator=DecisionTreeRegressor(),
param_grid={'max_depth': [1, 2, 3, 4]},
scoring='neg_mean_squared_error'),
'GrLivArea': GridSearchCV(cv=3, estimator=DecisionTreeRegressor(),
param_grid={'max_depth': [1, 2, 3, 4]},
scoring='neg_mean_squared_error')}
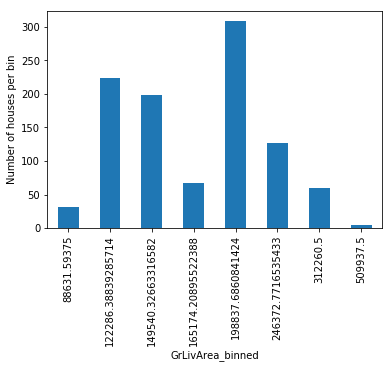
在使用决策树离散化时,每个区间,即在这种情况下每个预测值,不一定包含相同数量的观测值。让我们通过可视化来检查这一点:
import matplotlib.pyplot as plt
train_t.groupby('GrLivArea')['GrLivArea'].count().plot.bar()
plt.ylabel('Number of houses')
plt.show()
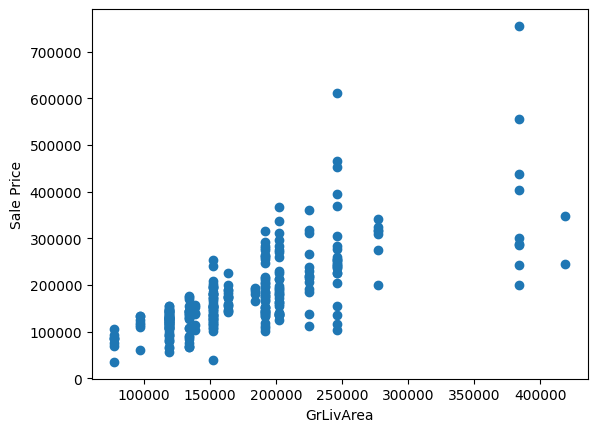
最后,我们可以确定在变换后是否与目标具有单调关系:
plt.scatter(test_t['GrLivArea'], y_test)
plt.xlabel('GrLivArea')
plt.ylabel('Sale Price')
plt.show()
四舍五入预测值#
有时,预测的输出在逗号后可能有多个值,这使得可视化和解释有些不便。幸运的是,我们可以通过 precision 参数来对这些值进行四舍五入:
disc = DecisionTreeDiscretiser(
bin_output="prediction",
precision=1,
cv=3,
scoring='neg_mean_squared_error',
variables=['LotArea', 'GrLivArea'],
regression=True)
disc.fit(X_train, y_train)
train_t= disc.transform(X_train)
test_t= disc.transform(X_test)
train_t.groupby('GrLivArea')['GrLivArea'].count().plot.bar()
plt.ylabel('Number of houses')
plt.show()
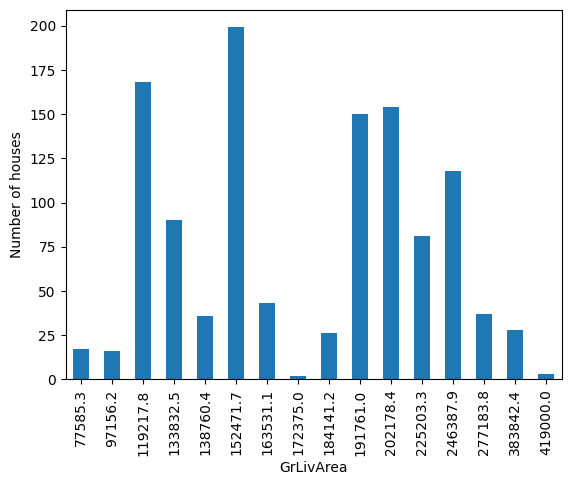
在这个例子中,我们正在预测房价,这是一个连续的目标。分类模型的过程是相同的,我们只需要将参数 regression 设置为 False。
离散化与区间限制#
在本节中,我们将返回区间的界限,而不是用决策树的预测值替换原始变量值。当返回区间边界时,我们需要将精度设置为正整数。
disc = DecisionTreeDiscretiser(
bin_output="boundaries",
precision=3,
cv=3,
scoring='neg_mean_squared_error',
variables=['LotArea', 'GrLivArea'],
regression=True)
# fit the transformer
disc.fit(X_train, y_train)
在这种情况下,当我们探索 binner_dict_ 属性时,我们将看到区间限制而不是决策树:
disc.binner_dict_
{'LotArea': [-inf, 8637.5, 10924.0, 13848.5, inf],
'GrLivArea': [-inf,
749.5,
808.0,
1049.0,
1144.5,
1199.0,
1413.0,
1438.5,
1483.0,
1651.5,
1825.0,
1969.5,
2386.0,
2408.0,
2661.0,
4576.0,
inf]}
在转换过程中,DecisionTreeDiscretiser() 将使用这些限制与 pandas.cut 来离散化连续变量的值:
train_t = disc.transform(X_train)
test_t = disc.transform(X_test)
print(train_t[['LotArea', 'GrLivArea']].head())
在以下输出中,我们看到了连续属性值被排序的区间限制:
LotArea GrLivArea
254 (-inf, 8637.5] (1199.0, 1413.0]
1066 (-inf, 8637.5] (1483.0, 1651.5]
638 (8637.5, 10924.0] (749.5, 808.0]
799 (-inf, 8637.5] (1651.5, 1825.0]
380 (-inf, 8637.5] (1651.5, 1825.0]
为了训练机器学习算法,我们将继续使用任何分类数据编码方法。
使用序数进行离散化#
在本指南的最后一部分,我们将用值被排序到的箱子的数量替换变量值。这里,0 是第一个箱子,1 是第二个,依此类推。
disc = DecisionTreeDiscretiser(
bin_output="bin_number",
cv=3,
scoring='neg_mean_squared_error',
variables=['LotArea', 'GrLivArea'],
regression=True,
)
# fit the transformer
disc.fit(X_train, y_train)
binner_dict_ 还将包含区间的界限:
disc.binner_dict_
{'LotArea': [-inf, 8637.5, 10924.0, 13848.5, inf],
'GrLivArea': [-inf,
749.5,
808.0,
1049.0,
1144.5,
1199.0,
1413.0,
1438.5,
1483.0,
1651.5,
1825.0,
1969.5,
2386.0,
2408.0,
2661.0,
4576.0,
inf]}
当我们应用转换时,DecisionTreeDiscretiser() 将使用这些限制与 pandas.cut 来离散化连续变量:
train_t = disc.transform(X_train)
test_t = disc.transform(X_test)
print(train_t[['LotArea', 'GrLivArea']].head())
在以下输出中,我们看到了连续属性的值被排序到的区间编号:
LotArea GrLivArea
254 0 5
1066 0 8
638 1 1
799 0 9
380 0 9
额外注意事项#
决策树离散化在底层使用 scikit-learn 的 DecisionTreeRegressor 或 DecisionTreeClassifier 来找到最佳区间限制。这些模型不支持缺失数据。因此,我们需要在继续进行离散化之前用数字替换缺失值。


