证据权重 (WoE)#
证据权重(Weight of Evidence,WoE)这一术语可以追溯到金融领域,特别是在1983年,它在描述信用风险分析和信用评分的关键组成部分中扮演了重要角色。自那时起,它已被用于医学研究、GIS研究等领域(详见以下参考文献)。
WoE 是一种基于贝叶斯定理和先验概率与后验概率概念的统计数据驱动方法,因此对数几率、事件和非事件的概念对于理解证据权重的运作方式至关重要。
WoE 仅针对二分类问题定义。换句话说,只有当目标变量为二元时,我们才能使用 WoE 对变量进行编码。
计算#
如何计算WoE?假设我们有一个数据集,其中有一个二元因变量,包含两个类别0和1,以及一个名为变量A的分类预测变量,包含三个类别(A1、A2和A3)。该数据集具有以下特征:
目标变量中有20个正例(1)和80个负例(0)。
类别 A1 有 10 个阳性病例和 15 个阴性病例。
A2 类别有 5 个阳性病例和 15 个阴性病例。
A3 类别有 5 个阳性病例和 50 个阴性病例。
首先,我们计算每个类别中目标值为正(1)的实例数量,然后将其除以数据中所有正实例的总数。接着,我们确定每个类别中目标值为0的实例数量,并将其除以数据集中所有负实例的总数:
对于类别 A1,我们有 10 个阳性病例和 15 个阴性病例,导致阳性比例为 10/20,阴性比例为 15/80。这意味着阳性比例是 0.5,阴性比例是 0.1875。
对于A2类别,我们在20个阳性病例中有5个阳性病例,这给我们一个阳性比率为5/20和一个阴性比率为15/80。这导致阳性比率为0.25,阴性比率为0.1875。
对于A3类别,我们在20个阳性病例中有5个阳性病例,导致阳性比例为5/20,阴性比例为50/80。因此,阳性比例为0.25,阴性比例为0.625。
现在我们计算每个类别中阳性病例比例的对数:
对于类别 A1,我们有 log (0.5/ 0.1875) = 0.98。
对于类别 A2,我们有 log (0.25/ 0.1875) = 0.28。
对于类别 A3,我们有 log (0.25/0.625) =-0.91。
最后,我们将自变量 A 的类别(A1、A2 和 A3)替换为 WoE 值:0.98、0.28、-0.91。
WoE 的特征#
WoE 的美妙之处在于,我们可以直接理解类别对成功概率(目标变量为1)的影响:
如果 WoE 值为负,则该类别中的负面案例多于正面案例。
如果 WoE 值为正,则该类别中的正例数量多于负例数量。
如果 WoE 为 0,那么该类别中正负案例的数量是相等的。
换句话说,对于WoE为正的类别,成功的概率较高;对于WoE为负的类别,成功的概率较低;而对于WoE为零的类别,两种目标结果的概率相等。
WoE 的用途#
通常,我们使用 WoE 来编码分类变量和数值变量。对于连续变量,我们首先需要进行分箱,即将变量排序到离散区间中。你可以通过使用 Feature-engine 的任何离散器对变量进行预处理来实现这一点。
一些作者已经将证据权重法扩展到神经网络和其他算法中,尽管他们展示了良好的结果,但当与逻辑回归模型一起使用时,证据权重法的预测建模性能更优(见下文参考文献)。
WoE 的局限性#
由于计算 WoE 的方法基于比率和对数,当 p(X=xj|Y = 1) = 0 或 p(X=xj|Y=0) = 0 时,WoE 值未定义。对于后者,除以 0 未定义,而对于前者,0 的对数未定义。
这种情况发生在类别仅显示目标可能值中的一个(要么总是取1,要么总是取0)。实际上,这主要发生在数据集中某个类别的频率较低时,即只有极少数观测显示该类别。
为了克服这一限制,可以考虑使用变量转换方法将这些类别分组,例如使用 Feature-engine 的 RareLabelEncoder()。
考虑到上述因素,作为数据科学和模型构建过程的一部分,进行详细的探索性数据分析(EDA)是至关重要的。将这些考虑和实践结合起来,不仅可以增强特征工程过程,还可以提高模型的性能。
未见类别#
在使用 WoE 时,我们定义映射,即使用训练集的观察结果为每个类别定义 WoE 值。如果测试集显示新的(未见过的)类别,我们将缺乏这些类别的 WoE 值,并且无法对它们进行编码。
这是一个已知问题,没有优雅的解决方案。如果新值出现在连续变量中,请考虑更改区间的大小和数量。如果未见类别出现在分类变量中,请在编码前考虑对低频类别进行分组。
WoEEncoder#
通过 WoEEncoder() ,您可以自动化计算给定特征集的证据权重过程。默认情况下,WoEEncoder() 将编码所有分类变量。您可以通过将变量名称列表传递给 variables 参数来仅编码子集。
默认情况下,WoEEncoder() 不会对数值变量进行编码,而是会引发错误。如果你想对数值变量进行编码,例如离散变量,请将 ignore_format 设置为 True。
WoEEncoder() 不会自动处理缺失值,因此在编码之前请确保用合适的值替换它们。你可以使用 Feature-engine 的插补器来填补缺失值。
WoEEncoder() 默认会忽略未见过的类别,在这种情况下,它们在编码后将被替换为 np.nan。你可以通过设置 unseen='raise' 来选择让编码器抛出一个错误。你也可以通过 fill_value 定义一个任意值来替换未见过的类别,尽管我们不推荐这个选项,因为它可能导致不可预测的结果。
Python 示例#
在文档的其余部分,我们将展示 WoEEncoder() 的功能。让我们看一个使用泰坦尼克号数据集的例子。
首先,让我们加载数据并将数据集分为训练集和测试集:
from sklearn.model_selection import train_test_split
from feature_engine.datasets import load_titanic
from feature_engine.encoding import WoEEncoder, RareLabelEncoder
X, y = load_titanic(
return_X_y_frame=True,
handle_missing=True,
predictors_only=True,
cabin="letter_only",
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0,
)
print(X_train.head())
我们在下面看到生成的数据框:
pclass sex age sibsp parch fare cabin embarked
501 2 female 13.000000 0 1 19.5000 M S
588 2 female 4.000000 1 1 23.0000 M S
402 2 female 30.000000 1 0 13.8583 M C
1193 3 male 29.881135 0 0 7.7250 M Q
686 3 female 22.000000 0 0 7.7250 M Q
在编码变量之前,我们将不常见的类别分组为一个类别,我们称之为’Rare’。为此,我们使用 RareLabelEncoder() 如下:
# set up a rare label encoder
rare_encoder = RareLabelEncoder(
tol=0.1,
n_categories=2,
variables=['cabin', 'pclass', 'embarked'],
ignore_format=True,
)
# fit and transform data
train_t = rare_encoder.fit_transform(X_train)
test_t = rare_encoder.transform(X_train)
请注意,我们传递 ignore_format=True 因为 pclass 是数值类型。
现在,我们设置 WoEEncoder() 来用证据权重替换类别,仅在指定的3个变量中:
# set up a weight of evidence encoder
woe_encoder = WoEEncoder(
variables=['cabin', 'pclass', 'embarked'],
ignore_format=True,
)
# fit the encoder
woe_encoder.fit(train_t, y_train)
通过 fit() 方法,编码器学习每个类别的证据权重,这些权重存储在其 encoder_dict_ 参数中:
woe_encoder.encoder_dict_
在 encoder_dict_ 中,我们找到了每个变量类别对应的 WoE(证据权重)。这样,我们可以将原始值映射到新值:
{'cabin': {'M': -0.35752781962490193, 'Rare': 1.083797390800775},
'pclass': {'1': 0.9453018143294478,
'2': 0.21009172435857942,
'3': -0.5841726684724614},
'embarked': {'C': 0.679904786667102,
'Rare': 0.012075414091446468,
'S': -0.20113381737960143}}
现在,我们可以继续对变量进行编码:
train_t = woe_encoder.transform(train_t)
test_t = woe_encoder.transform(test_t)
print(train_t.head())
下面我们看到的是用证据权重替换原始变量值后的结果数据集:
pclass sex age sibsp parch fare cabin embarked
501 0.210092 female 13.000000 0 1 19.5000 -0.357528 -0.201134
588 0.210092 female 4.000000 1 1 23.0000 -0.357528 -0.201134
402 0.210092 female 30.000000 1 0 13.8583 -0.357528 0.679905
1193 -0.584173 male 29.881135 0 0 7.7250 -0.357528 0.012075
686 -0.584173 female 22.000000 0 0 7.7250 -0.357528 0.012075
分类变量和数值变量中的 WoE#
在之前的例子中,我们只对变量 ‘cabin’, ‘pclass’, ‘embarked’ 进行了编码,其余变量保持不变。在下面的例子中,我们将使用 Feature-engine 的管道按顺序转换变量。我们将对分类变量中的稀有类别进行分组。接下来,我们将离散化数值变量。最后,我们将使用 WoE 对它们进行编码。
首先,让我们加载数据并将其分为训练集和测试集:
from sklearn.model_selection import train_test_split
from feature_engine.datasets import load_titanic
from feature_engine.encoding import WoEEncoder, RareLabelEncoder
from feature_engine.pipeline import Pipeline
from feature_engine.discretisation import EqualFrequencyDiscretiser
X, y = load_titanic(
return_X_y_frame=True,
handle_missing=True,
predictors_only=True,
cabin="letter_only",
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0,
)
print(X_train.head())
我们在下面看到生成的数据集:
pclass sex age sibsp parch fare cabin embarked
501 2 female 13.000000 0 1 19.5000 M S
588 2 female 4.000000 1 1 23.0000 M S
402 2 female 30.000000 1 0 13.8583 M C
1193 3 male 29.881135 0 0 7.7250 M Q
686 3 female 22.000000 0 0 7.7250 M Q
让我们用分类变量和数值变量来定义列表:
现在,我们将设置流水线,首先离散化数值变量,然后将罕见标签和低频区间分组到一个公共组中,最后使用 WoE 对所有变量进行编码:
我们已经创建了一个变量转换管道,包含以下步骤:
首先,我们使用
EqualFrequencyDiscretiser()对数值变量进行分箱处理。接下来,我们使用
RareLabelEncoder()将不常见的类别和区间分组为一个组。最后,我们使用
WoEEncoder()将所有变量中的值替换为证据权重。
现在,我们可以继续将管道拟合到训练集,以便不同的转换器学习变量转换的参数。
X_trans_t = pipe.fit_transform(X_train, y_train)
print(X_trans_t.head())
我们在下面看到生成的数据框:
pclass sex age sibsp parch fare cabin \
501 0.210092 1.45312 0.319176 -0.097278 0.764646 0.020285 -0.357528
588 0.210092 1.45312 0.319176 0.458001 0.764646 0.248558 -0.357528
402 0.210092 1.45312 0.092599 0.458001 -0.161255 -0.133962 -0.357528
1193 -0.584173 -0.99882 -0.481682 -0.097278 -0.161255 0.020285 -0.357528
686 -0.584173 1.45312 0.222615 -0.097278 -0.161255 0.020285 -0.357528
embarked
501 -0.201134
588 -0.201134
402 0.679905
1193 0.012075
686 0.012075
最后,我们可以将 WoE 编码变量的值与原始值进行可视化,以验证其符合 S 形函数形状,这是 WoE 预期的行为:
import matplotlib.pyplot as plt
age_woe = pipe.named_steps['woe'].encoder_dict_['age']
sorted_age_woe = dict(sorted(age_woe.items(), key=lambda item: item[1]))
categories = [str(k) for k in sorted_age_woe.keys()]
log_odds = list(sorted_age_woe.values())
plt.figure(figsize=(10, 6))
plt.bar(categories, log_odds, color='skyblue')
plt.xlabel('Age')
plt.ylabel('WoE')
plt.title('WoE for Age')
plt.grid(axis='y')
plt.show()
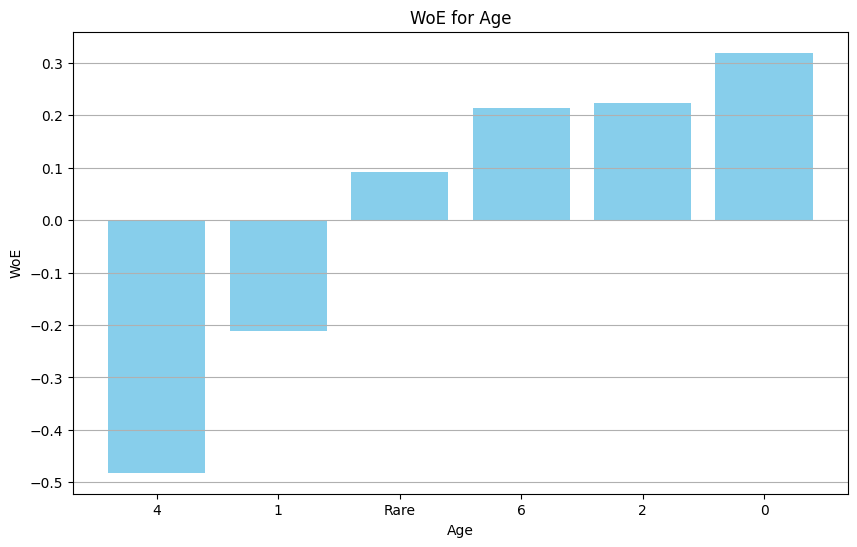
在下图中,我们可以看到变量 ‘age’ 不同类别的 WoE:
WoE 值在 y 轴上,类别在 x 轴上。我们看到 WoE 值是单调递增的,这是 WoE 的预期行为。如果我们看类别 4,我们可以看到 WoE 大约是 -0.45,这意味着在这个年龄段中,与负案例(非幸存者)相比,正案例(幸存者)的比例较小。换句话说,这个年龄区间内的人生存概率较低。
将模型添加到管道中#
为了完成演示,我们可以在管道中添加一个逻辑回归模型,以在变量转换后获得生存预测。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
pipe = Pipeline(
[
("disc", EqualFrequencyDiscretiser(variables=numerical_features)),
("rare_label", RareLabelEncoder(tol=0.1, n_categories=2, variables=all, ignore_format=True)),
("woe", WoEEncoder(variables=all)),
('model', LogisticRegression(random_state=0)),
])
pipe.fit(X_train, y_train)
y_pred = pipe.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
模型的准确性如下所示:
Accuracy: 0.76
模型的准确率为0.76,对于第一个模型来说这是一个不错的结果。我们可以通过调整逻辑回归模型的超参数来改进模型。请注意,由于数据集不平衡,准确率可能不是此问题的最佳指标。我们建议使用其他指标,如F1分数、精确度、召回率或ROC-AUC分数。您可以在我们的`课程 <https://www.trainindata.com/p/machine-learning-with-imbalanced-data>`_中了解更多关于不平衡数据集的信息。
证据权重和信息价值#
WoE 的一个常见扩展是信息值(IV),它是衡量变量预测能力的一个指标。IV 的计算方法如下:
其中,pi 是第 i 类中阳性病例的百分比,qi 是第 i 类中阴性病例的百分比,而 WoE_{i} 是第 i 类的证据权重。
IV 是衡量变量预测能力的一个指标。IV 值越高,变量的预测能力越强。因此,WoE 与信息值的结合可以用于二分类问题的特征选择。
特征工程中的证据权重和信息价值#
如果你在问自己 Feature-engine 是否允许你自动化这个过程,答案是:当然可以!你可以使用 SelectByInformationValue() 类,它将为你处理所有这些步骤。再次提醒,请记住给定的注意事项。