PowerTransformer#
幂变换是一组用于将数值变量转换为更适合建模形状的数学函数。变换函数通常表示为 \(x' = x^{\lambda}\),其中 \(x\) 是原始变量,:math:`lambda`(lambda)是变换参数。
这些变换有助于稳定方差,使数据呈现出更接近正态分布的形状,和/或改善关系的线性性。
使用幂变换#
幂变换对于满足统计测试和需要变量间线性关系及同方差性(值间常数方差)的模型的假设特别有用。它们还可以帮助减少数据中的偏斜,即通过归一化分布。
幂变换与缩放器不同,它们修改数据的分布,通常是为了稳定方差和归一化分布,而缩放器只是调整数据的比例,而不改变其基础分布。
简而言之,幂函数为数据分析提供了优秀的工具包,特别是在线性模型(回归或分类)方面。
幂变换的特殊情况#
大多数变量变换,如对数、倒数和平方根,都是幂变换的特例,其中指数(lambda)分别为0、-1和0.5。
你可以使用 PowerTransformer 应用这些变换,正如我们将在本页后面看到的那样,或者通过专门的变换器,如 LogTransformer 和 ReciprocalTransformer。
我应该选择哪个lambda?#
幂变换的挑战在于找到合适的 lambda 值进行变换。通常,这包括试错法,或使用像 Box-Cox 或 Yeo-Johnson 变换这样的泛化函数。
作为一般指导原则,如果变量是右偏的,我们会使用 lambda < 1,如果变量是左偏的,我们会使用 lambda > 1。
Box-Cox 变换#
Box-Cox 变换是一种幂变换的泛化,它找到一个最优的 lambda 来稳定方差并使数据更接近正态分布。这种变换只接受正值。
Feature-engine 的 BoxCoxTransformer() 应用了 Box-Cox 变换。
Yeo-Johnson 变换#
Yeo-Johnson 变换扩展了 Box-Cox 变换,使其能够处理正负值,以找到变换的最佳 lambda 值。
YeoJohnsonTransformer() 应用 Yeo-Johnson 变换。
Python 示例#
PowerTransformer() 对数值型自变量应用幂变换。我们将使用 Ames House Prices 数据集来查看它的实际应用。首先,让我们加载数据集并将其拆分为训练集和测试集:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from feature_engine.transformation import PowerTransformer
# Load dataset
X, y = fetch_openml(name='house_prices', version=1, return_X_y=True, as_frame=True)
X.set_index('Id', inplace=True)
# Separate into train and test sets
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
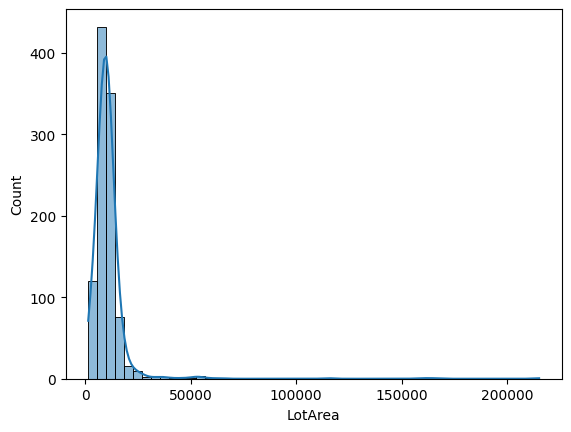
现在,让我们可视化 LotArea 变量的分布:
sns.histplot(X_train['LotArea'], kde=True, bins=50)
在以下输出中,我们可以看到原始特征分布是高度右偏的:
找到合适的幂变换 lambda 值是具有挑战性的,通常需要通过试错法来实现。因此,让我们从尝试默认系数(lambda)开始,即 0.5(也就是说,我们正在应用平方根变换):
# Set up the variable transformer (tf)
tf = PowerTransformer(variables = ['LotArea', 'GrLivArea'])
# Fit the transformer
X_train_transformed = tf.fit_transform(X_train)
# Plot histogram
sns.histplot(X_train_transformed['LotArea'], kde=True, bins=50)
以下是转换后的特征分布:
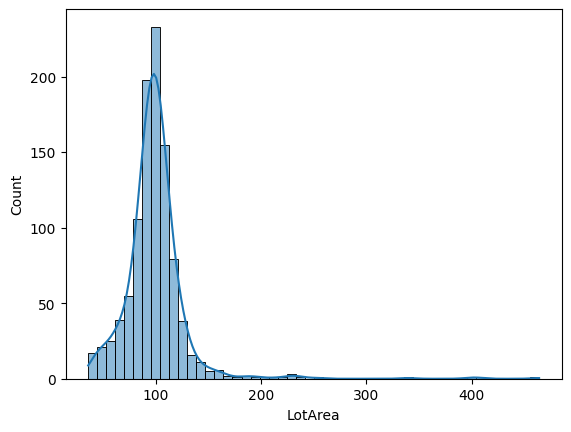
看起来更好了,对吧!?它仍然是右偏的,但变异较小(我们很快就会确认这一点)。现在,让我们尝试为参数 λ(exp)传递一个“最佳值”。
# Set up the variable transformer (tf)
tf_custom = PowerTransformer(variables = ['LotArea', 'GrLivArea'], exp=0.001)
# Fit the transformer
X_train_transformed_custom = tf_custom.fit_transform(X_train)
# Plot histogram
sns.histplot(X_train_transformed_custom['LotArea'], kde=True, bins=50)
在以下输出中,我们可以看到数据现在具有更类似高斯分布的形状,并且方差似乎更低。因此,我们可以看到通过使用自定义 lambda 函数,我们可以转换变量的分布:
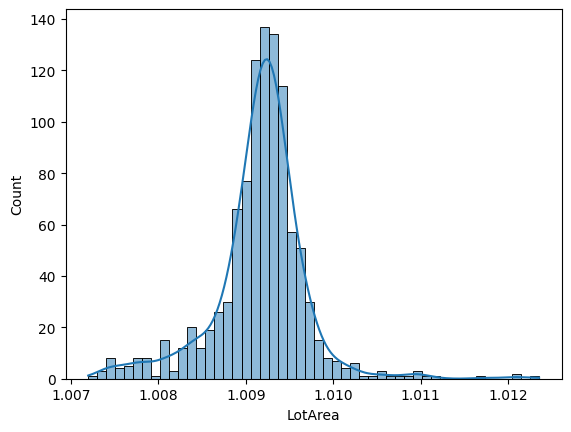
幂变换预计会重塑数据分布,减少极端异常值的影响,从而降低方差。
由于幂变换改变了数据的尺度,我们无法直接比较方差。相反,我们将计算变异系数(CV)。样本的CV定义为标准差与均值的比值,表示为 \(CV = \left(\frac{s}{\overline{x}}\right)\)。
现在让我们使用CV来评估数据转换对变异性的影响。
# Compute coefficient of variation (CV)
def compute_cv(data):
"""Compute the coefficient of variation (CV) for a given dataset."""
return np.std(data, ddof=1) / np.mean(data) if np.mean(data) != 0 else np.inf
cv_raw_data = compute_cv(X_train['LotArea'])
cv_transformed_data = compute_cv(X_train_transformed['LotArea'])
cv_transformed_data_custom = compute_cv(X_train_transformed_custom['LotArea'])
print(f"""
Raw data CV: {cv_raw_data:.2%}
Transformed data exp:0.5 CV: {cv_transformed_data:.2%}
Transformed data exp:0.001 CV (custom): {cv_transformed_data_custom:.2%}
""")
在以下输出中,我们可以看到原始数据和转换后的数据的最终简历:
Raw data CV: 105.44%
Transformed data exp:0.5 CV: 30.91%
Transformed data exp:0.001 CV (custom): 0.05%
通过比较原始数据和转换后数据的变异系数(CV),可以明显看出转换的效果。原始CV的CV值大于1(100%),这意味着方差大于均值(由于数据高度偏斜)。使用平方根转换(默认exp参数)的结果是CV约为31%。最后,使用较低exp参数值的幂转换得到了0.05%的CV,远低于原始数据和平方根转换后的数据。
值得注意的是,尽管表现出较低的变异系数(CV),该系数衡量的是相对于均值的变异性,但一个特征仍可以保留足够的绝对方差,从而有效地贡献于机器学习模型的性能,特别是在依赖于数据变异性假设的算法中,如线性回归和其他基于回归的模型。
根据分布选择lambda#
在本节中,我们将进一步探讨lambda参数对左偏和右偏分布的影响。
首先,让我们用这些分布创建一个玩具数据集:
# Set random seed for reproducibility
np.random.seed(42)
# Generating right-skewed data using exponential distribution
right_skewed_data = np.random.exponential(scale=2, size=1000)
# Generating left-skewed data by flipping the right-skewed data
left_skewed_data = -np.random.gamma(shape=2, scale=2, size=1000) \
+ np.max(np.random.gamma(shape=2, scale=2, size=1000))
# Create dataframe with simulated data
df_sim = pd.DataFrame({
'left_skewed': left_skewed_data,
'right_skewed': right_skewed_data}
)
# Plotting the distributions
fig, axes = plt.subplots(ncols=2, figsize=(12, 4))
hist_params = dict(kde=True, bins=30, alpha=0.7)
sns.histplot(df_sim.left_skewed, ax=axes[0], color='blue', **hist_params)
sns.histplot(df_sim.right_skewed, ax=axes[1], color='red', **hist_params)
axes[0].set_title('Left-skewed data')
axes[1].set_title('Right-skewed data')
plt.show()
我们在以下输出中看到我们创建的变量的分布:
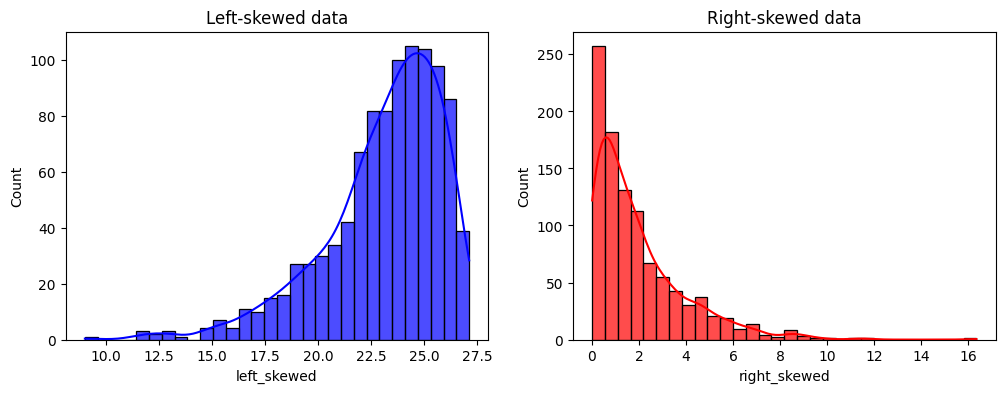
现在,让我们使用 PowerTransformer() 转换数据,使用默认的 lambda 参数(exp = 0.5):
# Set up the variable transformer (tf)
tf = PowerTransformer(variables = ['left_skewed', 'right_skewed'])
# Fit the transformer
df_sim_transformed = tf.fit_transform(df_sim)
# Plot histograms
fig,axes = plt.subplots(ncols=2, figsize=(12,4))
sns.histplot(
df_sim_transformed['left_skewed'], ax=axes[0], color='blue', **hist_params
)
sns.histplot(
df_sim_transformed['right_skewed'], ax=axes[1], color='red', **hist_params
)
axes[0].set_title('Transformed left-skewed data')
axes[1].set_title('Transformed right-skewed data')
plt.show()
在以下输出中,我们可以看到每个转换变量的分布:
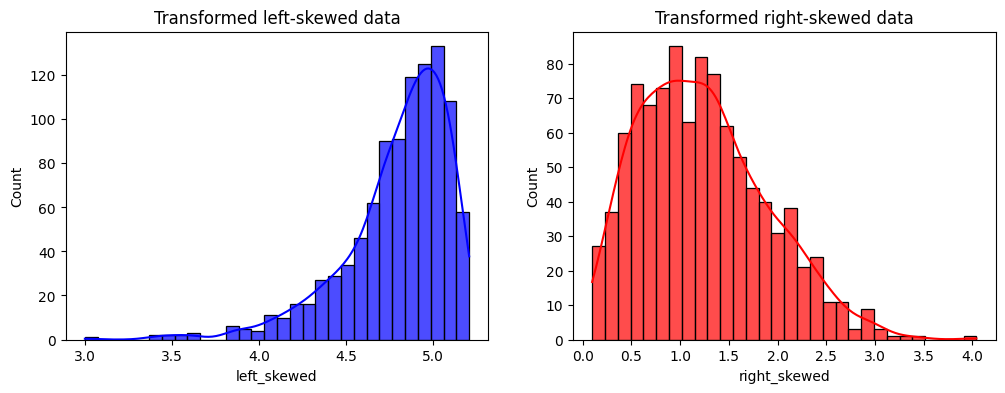
它改进了分发,但我们还能做得更好!
根据我们之前提到的指南,我们将对右偏分布使用 lambda <1,对左偏分布使用 lambda >1:
# Set up the variable transformer (tf)
tf_right = PowerTransformer(variables = ['right_skewed'], exp=0.246)
tf_left = PowerTransformer(variables = ['left_skewed'], exp=4.404)
# Fit the transformers
tf_right.fit(df_sim)
tf_left.fit(df_sim)
# Plot histograms
fig,axes = plt.subplots(ncols=2, figsize=(12,4))
sns.histplot(
tf_left.transform(df_sim)['left_skewed'], ax=axes[0],
color='blue', **hist_params
)
sns.histplot(
tf_right.transform(df_sim)['right_skewed'], ax=axes[1],
color='red', **hist_params
)
axes[0].set_title('Transformed left-skewed data')
axes[1].set_title('Transformed right-skewed data')
plt.show()
在以下输出中,我们看到了转换变量的分布:
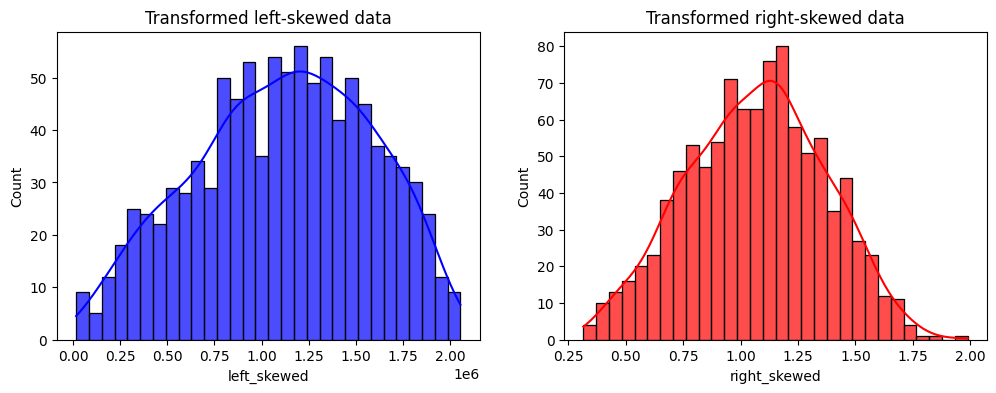
现在,分布看起来更像是一个高斯分布了 :)
逆变换#
Feature-engine 的功率变换器可以反向变换以获得原始数据表示。例如,如果我们应用平方根变换,变换器可以将变换后的数据平方以获得原始变量。这对于解释机器学习模型的结果和展示数据分析的结果非常有用。
在本节中,我们将研究如何使用逆变换。
首先,让我们再次拟合变换器:
# Set up the variable transformer (tf)
tf = PowerTransformer(variables = ['left_skewed', 'right_skewed'])
# Fit the transformer
df_sim_transformed = tf.fit_transform(df_sim)
现在,让我们看看原始数据的前几行:
df_sim.head(3)
在以下输出中,我们看到了原始数据的前几行:
left_skewed right_skewed
0 23.406936 0.938536
1 26.282836 6.020243
2 22.222784 2.633491
让我们看看转换后的数据的前几行:
df_sim_transformed.head(3)
在以下输出中,我们看到了转换后的数据的前几行:
left_skewed right_skewed
0 4.838072 0.968781
1 5.126679 2.453618
2 4.714105 1.622804
最后,让我们看看如何反转变换以获得原始值:
tf.inverse_transform(df_sim_transformed).head(3)
逆变换的结果:
left_skewed right_skewed
0 23.406936 0.938536
1 26.282836 6.020243
2 22.222784 2.633491
正如我们所见,原始数据和逆变换后的数据是相同的。
考虑事项#
幂变换是将数据转换为满足统计测试和线性回归模型假设的强大工具。
在实践中,我们会使用 BoxCoxTransformer() 或 YeoJohnsonTransformer(),因为它们会自动找到最适合的 lambda 进行转换。但自动化并不总是更好。通常这些转换并不能返回期望的输出。
我们应始终对变换进行分析,比较原始分布和变换后的分布,以确保我们获得预期的结果。
附加资源#
你可以在以下位置找到更多关于 PowerTransformer() 的详细信息:
有关此方法和其他特征工程方法的更多详细信息,请查看以下资源:

机器学习的特征工程#
或者阅读我们的书:

Python 特征工程手册#
我们的书籍和课程都适合初学者和更高级的数据科学家。通过购买它们,您正在支持 Feature-engine 的主要开发者 Sole。
