互惠变换器#

互逆变换涉及将每个数据值 x 替换为其倒数，即 1/x。这种变换对于处理异方差性很有用，异方差性是指回归模型中的误差在自变量的不同值之间变化，并且可以将偏斜的分布转换为更对称的分布。它还可以线性化某些非线性关系，使它们更容易用线性回归建模，并通过减少异常值的影响或使残差标准化来改善线性模型的整体拟合。

应用程序#

互逆变换对于比率非常有用，其中变量的值由两个变量的除法结果产生。一些例子包括学生-教师比率（每名教师的学生数）或作物产量（每英亩吨数）等变量。

通过计算这些变量的倒数，我们将从每名教师的学生数转换为每名学生的教师数，或者从每英亩的吨数转换为每吨的英亩数。这种转换仍然符合直觉，并且可以使数值的分布更接近正态分布，从而更好地展开。

属性#

  • x 的互逆变换是 1 / x

  • 倒数变换的逆变换也是倒数变换

  • 反比例函数的值域包括所有实数，除了 0。

虽然在理论上，倒数函数对正负值都定义了，但在实际应用中，它主要用于转换严格正的变量。

互惠变换器#

The ReciprocalTransformer 对数值变量应用倒数变换。默认情况下，它将查找并转换数据集中的所有数值变量。更好的做法是将其应用于选定的一组变量，您可以通过在设置转换器时向 variables 参数传递包含变量名称的列表来实现这一点。

如果任何变量的值为 0，转换器将会引发错误。

Python 示例#

在接下来的章节中，我们将演示如何使用 ReciprocalTransformer 应用互逆变换。

我们将加载Ames房价数据集，并创建一个新变量，表示房屋车库中每辆车的平方英尺数。接下来，我们将数据分为训练集和测试集：

import matplotlib.pyplot as plt

from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from feature_engine.transformation import ReciprocalTransformer

data = fetch_openml(name='house_prices', as_frame=True)
data = data.frame

data["sqrfootpercar"] = data['GarageArea'] / data['GarageCars']
data = data[~data["sqrfootpercar"].isna()]

y = data['SalePrice']
X = data[['GarageCars', 'GarageArea', "sqrfootpercar"]]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42)

print(X_train.head())

在以下输出中，我们看到了生成的数据集：

      GarageCars  GarageArea  sqrfootpercar
1170           1         358          358.0
330            1         352          352.0
969            1         264          264.0
726            2         540          270.0
1308           2         528          264.0

让我们绘制车库中每辆车平方英尺面积的分布图：

X_train["sqrfootpercar"].hist(bins=50, figsize=(4,4))
plt.title("sqrfootpercar")
plt.show()

在下图中，我们可以看到变量的偏斜度：

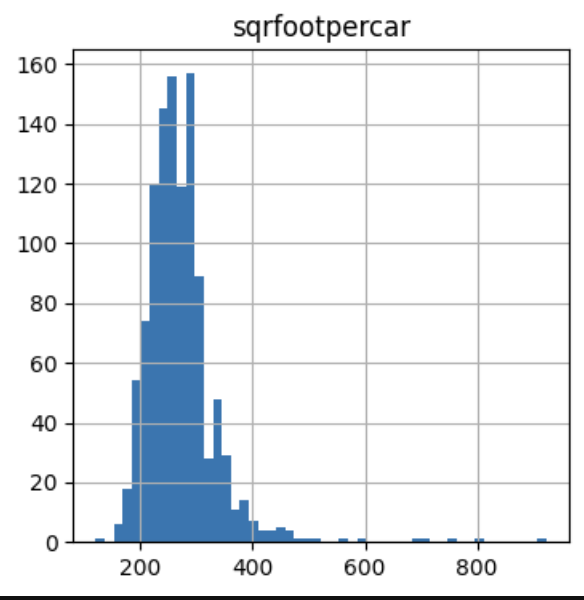
../../_images/reciprocal_transfomer_original.png

现在让我们对这个变量应用互逆变换：

tf = ReciprocalTransformer(variables="sqrfootpercar")

train_t = tf.fit_transform(X_train)
test_t = tf.transform(X_test)

最后，让我们绘制倒数变换后的分布图：

train_t["sqrfootpercar"].hist(bins=50, figsize=(4,4))
plt.title("sqrfootpercar")
plt.show()

在下图中，我们可以看到，倒数变换使得变量的值更接近对称或正态分布：

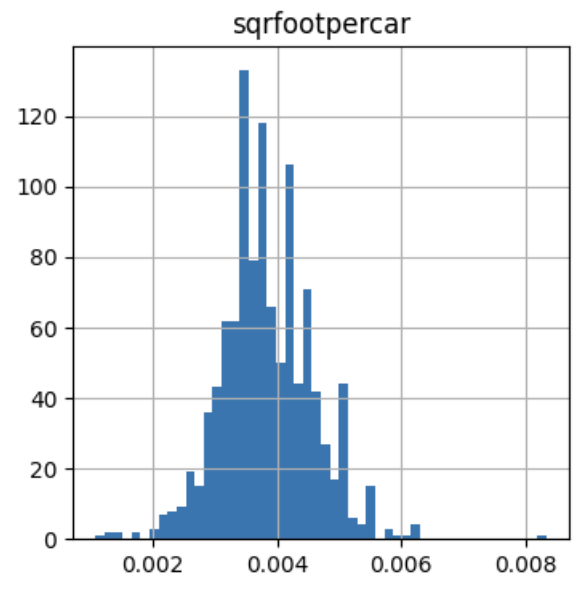
../../_images/reciprocal_transfomer_new.png

逆变换#

通过 ReciprocalTransformer，我们可以使用 inverse_transform 方法轻松地将转换后的数据恢复为其原始表示。

train_unt = tf.inverse_transform(train_t)
test_unt = tf.inverse_transform(test_t)

让我们检查一下反转的变换：

train_unt["sqrfootpercar"].hist(bins=50, figsize=(4,4))
plt.title("sqrfootpercar")
plt.show()

如以下图像所示，我们通过重新应用反函数到变换后的变量，获得了原始数据：

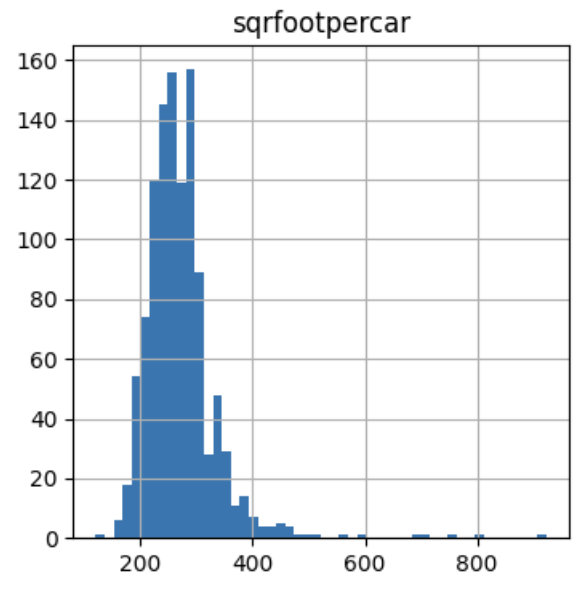
../../_images/reciprocal_transfomer_inverse.png

转换流程#

如前所述，互逆变换通常适用于比率变量，因此我们需要使用其他类型的变换来转换数据集中的其他变量。

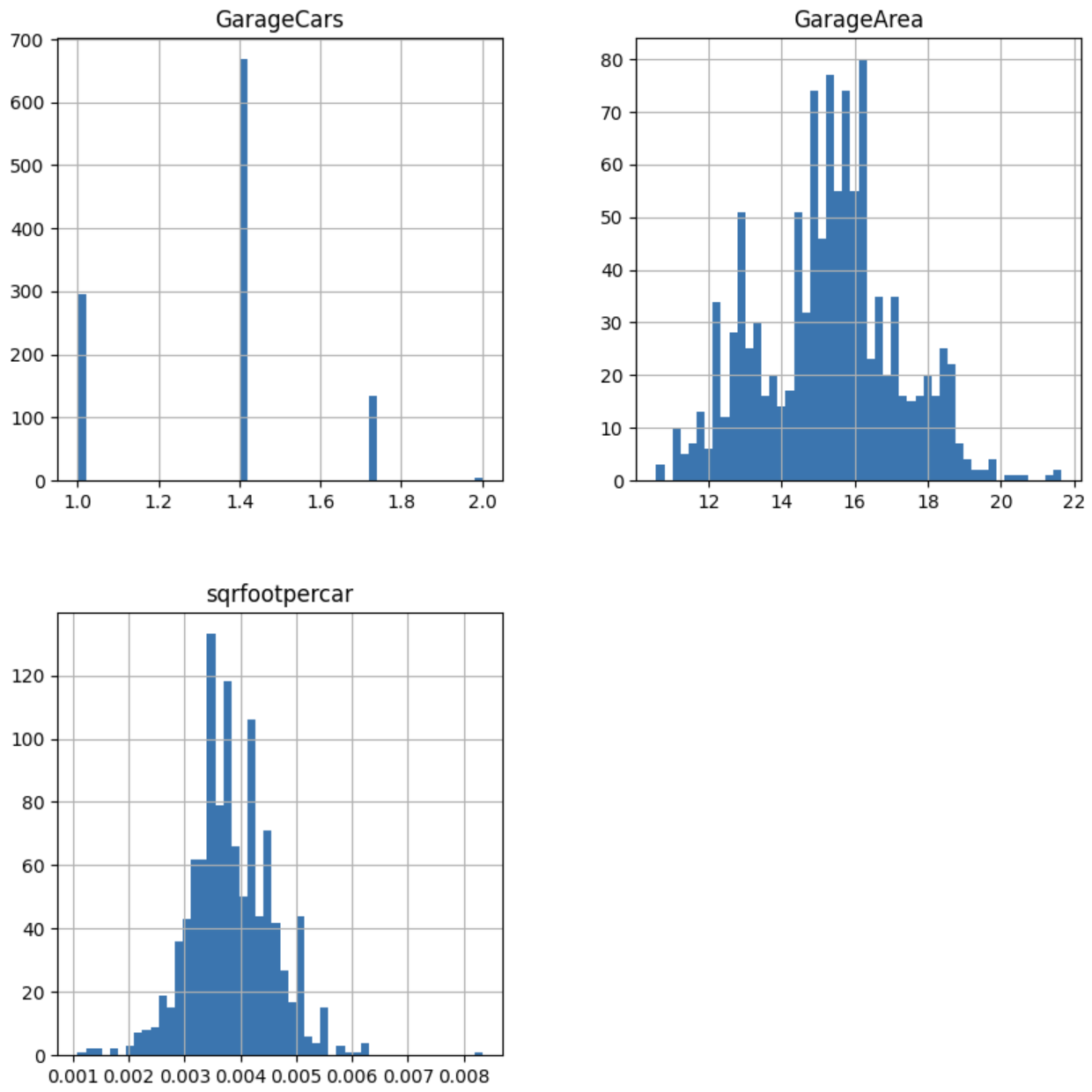
让我们不要绘制原始数据中3个变量的分布，以查看哪些变换可能适合它们：

X_train.hist(bins=50, figsize=(10,10))
plt.show()

在下图中，我们可以看到，正如预期的那样，GarageCounts 包含计数（可能遵循泊松分布），而 GarageArea 是一个连续变量：

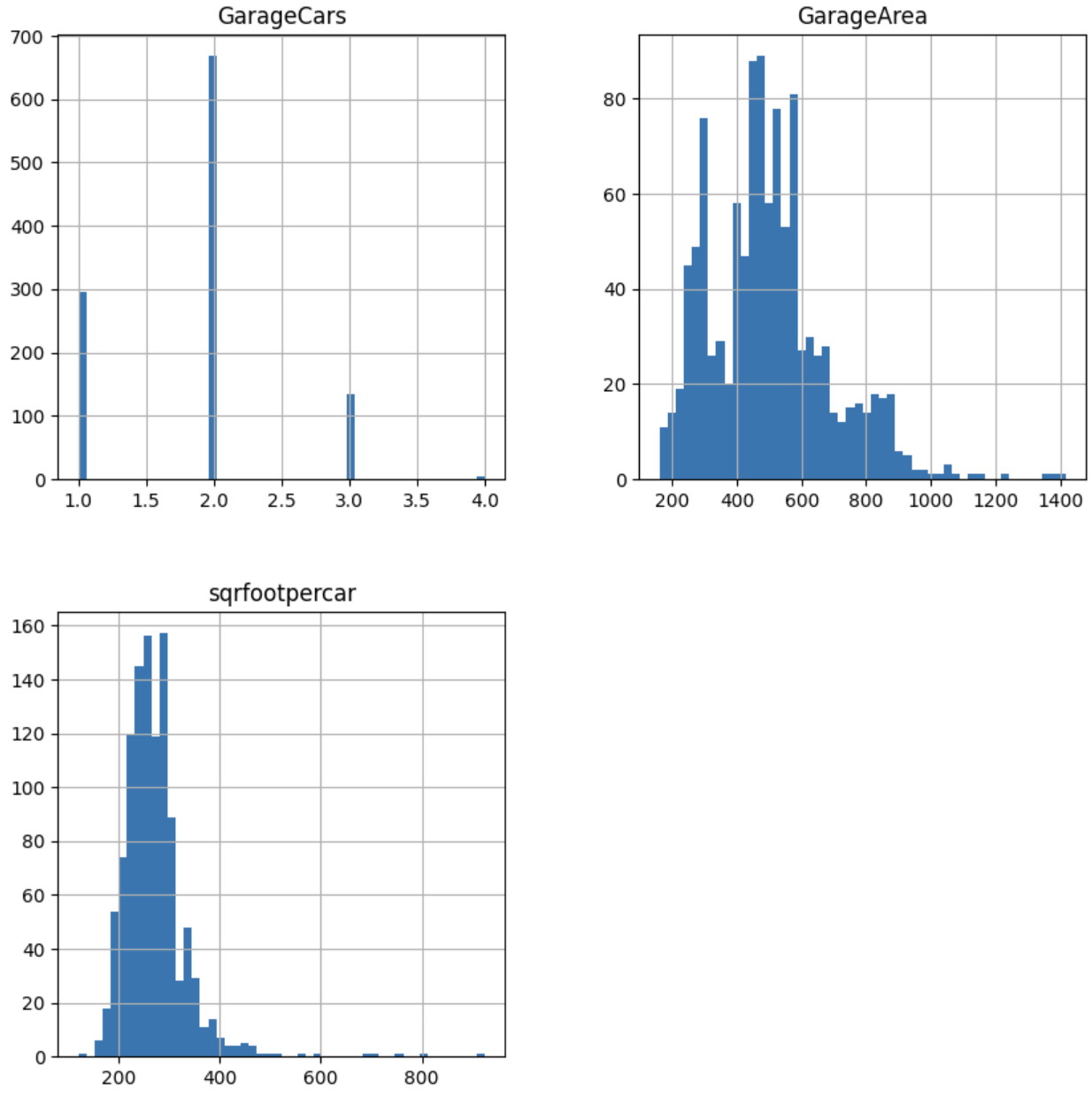
../../_images/reciprocal_transformer_3plots_original.png

接下来，我们创建一个管道，对 GarageCounts 应用平方根变换，对 GarageArea 应用 Box-Cox 变换，同时对 “sqrfootpercar” 应用倒数变换：

from feature_engine.pipeline import Pipeline
from feature_engine.transformation import PowerTransformer, BoxCoxTransformer

from feature_engine.pipeline import Pipeline
from feature_engine.transformation import PowerTransformer, BoxCoxTransformer

pipe = Pipeline([
    ("reciprocal", ReciprocalTransformer(variables="sqrfootpercar")),
    ("sqrroot", PowerTransformer(variables="GarageCars", exp=1/2)),
    ("boxcox", BoxCoxTransformer(variables="GarageArea")),
])

现在让我们拟合管道并转换数据集：

train_t = pipe.fit_transform(X_train)
test_t = pipe.transform(X_test)

现在，我们可以通过绘制变换后数据的直方图来验证这些变换如何改善了所有变量之间的值分布：

train_t.hist(bins=50, figsize=(10,10))
plt.show()

在下图中，我们可以看到变量不再显示右偏性，现在它们的值在其值范围内分布得更加对称：

../../_images/reciprocal_transformer_3plots_new.png

就是这样！我们现在已经在数据集中对变量应用了不同的数学函数来稳定方差。

互反函数的替代方案#

我们提到，在实际应用中，反函数用于正数值。如果变量包含负值，Yeo-Johnson 变换，或加上一个常数后再进行 Box-Cox 变换可能是更好的选择。

如果变量不是来自比率，那么可以使用对数变换或反正弦变换来处理这些情况。

如果变量包含计数，那么平方根变换更为合适。

Box-Cox 变换通过自动探索多个函数来自动化寻找最佳变换的过程。

所有这些函数都被认为是方差稳定变换，并且被设计用来转换数据，以满足统计参数检验和线性回归模型的假设。

你可以通过Feature-engine的转换模块中的转换器直接应用所有这些功能。记住在转换后进行适当的数据分析，以确保转换达到了预期效果，否则，我们只是在特征工程管道中增加了复杂性，而没有增加实际的好处。

Feature-engine 的替代方案#

你可以使用以下转换器应用其他方差数据变换函数：

附加资源#

你可以在以下位置找到更多关于 ReciprocalTransformer() 的详细信息：

有关此方法和其他特征工程方法的更多详细信息，请查看以下资源：

../../_images/feml.png

机器学习的特征工程#











或者阅读我们的书：

../../_images/cookbook.png

Python 特征工程手册#














我们的书籍和课程都适合初学者和更高级的数据科学家。通过购买它们，您正在支持 Feature-engine 的主要开发者 Sole。

On this page
显示源代码