BoxCoxTransformer#

Box-Cox 变换是幂变换族的推广，定义如下：

y = (x**λ - 1) / λ,      for λ != 0
y = log(x),              for λ = 0

这里，y 是变换后的数据，x 是待变换的变量，λ 是变换参数。

Box Cox 变换用于减少或消除变量的偏斜，并获得更接近正态分布的特征。

Box Cox 变换评估了常用的变换。当 λ = 1 时，我们得到原始变量；当 λ = 0 时，我们得到对数变换；当 λ = -1 时，我们得到倒数变换；当 λ = 0.5 时，我们得到平方根变换。

Box-Cox 变换通过最大似然估计评估多个 λ 值，并选择最优的 λ 参数值，该值返回最佳变换。最佳变换发生在变换后的数据更好地接近正态分布时。

Box Cox 变换是为严格正变量定义的。如果你的变量不是严格正的，你可以添加一个常数或使用 Yeo-Johnson 变换代替。

Box Cox 变换的用途#

我们在数据分析中使用的许多统计方法都对数据做出了假设。例如，线性回归模型假设因变量的值是独立的，响应变量与自变量之间存在线性关系，并且残差是正态分布且以0为中心。

当这些假设不成立时，我们无法完全信任回归分析的结果。为了使数据符合假设并提高对模型的信任度，在数据科学项目中，通常的做法是在分析之前对变量进行转换。

在时间序列预测中，我们使用 Box Cox 变换使非平稳时间序列变为平稳。

参考文献#

George Box 和 David Cox。“变换的分析”。在1964年的一个研究会议上宣读。https://rss.onlinelibrary.wiley.com/doi/abs/10.1111/j.2517-6161.1964.tb00553.x

BoxCoxTransformer#

The BoxCoxTransformer() 对数值变量应用BoxCox变换。它在底层使用 SciPy.stats 来应用变换。

BoxCox 变换仅适用于严格正变量 (>=0)。如果变量包含 0 或负值，BoxCoxTransformer() 将返回错误。要将此变换应用于非正变量，您可以添加一个常数值。或者，您可以使用 YeoJohnsonTransformer() 应用 Yeo-Johnson 变换。

Python 代码示例#

在本节中，我们将对 Ames 房价数据集中的两个变量应用此数据转换。

首先，我们导入模块、类和函数，然后加载房价数据集并将其分为训练集和测试集。

import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split

from feature_engine.transformation import BoxCoxTransformer

data = fetch_openml(name='house_prices', as_frame=True)
data = data.frame

X = data.drop(['SalePrice', 'Id'], axis=1)
y = data['SalePrice']


X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42)

print(X_train.head())

在以下输出中，我们看到了房价数据集的预测变量：

      MSSubClass MSZoning  LotFrontage  LotArea Street Alley LotShape  \
         20       RL         70.0     8400   Pave   NaN      Reg
        60       RL         59.0     7837   Pave   NaN      IR1
         30       RL         67.0     8777   Pave   NaN      Reg
         50       RL         60.0     7200   Pave   NaN      Reg
         50       RL         50.0     5000   Pave  Pave      Reg

     LandContour Utilities LotConfig  ... ScreenPorch PoolArea PoolQC  Fence  \
        Lvl    AllPub    Inside  ...           0        0    NaN    NaN
       Lvl    AllPub    Inside  ...           0        0    NaN    NaN
        Lvl    AllPub    Inside  ...           0        0    NaN  MnPrv
        Lvl    AllPub    Corner  ...           0        0    NaN  MnPrv
        Lvl    AllPub    Inside  ...           0        0    NaN    NaN

     MiscFeature MiscVal  MoSold  YrSold  SaleType  SaleCondition
        NaN       0       6    2010        WD         Normal
       NaN       0       5    2009        WD         Normal
        NaN       0       5    2008        WD         Normal
        NaN       0       6    2007        WD         Normal
        NaN       0       5    2010        WD         Normal

[5 rows x 79 columns]

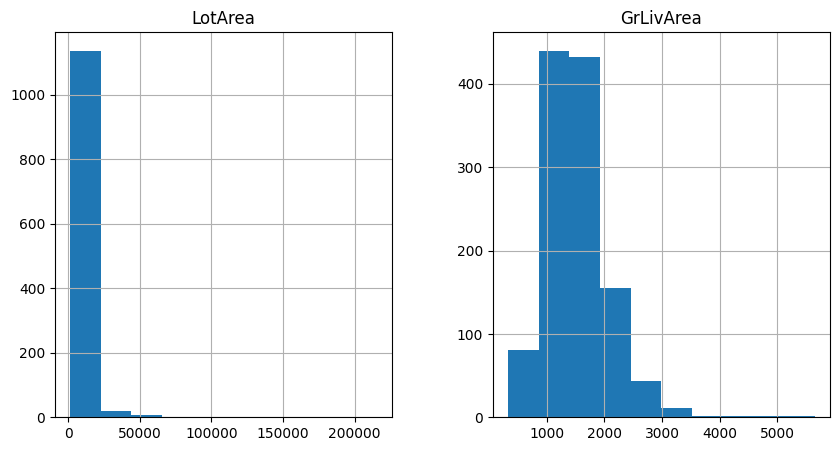
让我们用直方图检查原始数据中两个变量的分布。

X_train[['LotArea', 'GrLivArea']].hist(figsize=(10,5))
plt.show()

在下图中，我们可以看到变量是非正态分布的：

现在我们对指示的2个变量应用BoxCox变换。首先，我们设置变换器并将其拟合到训练集，以便找到最佳的lambda值。

boxcox = BoxCoxTransformer(variables = ['LotArea', 'GrLivArea'])
boxcox.fit(X_train)

通过 fit()，BoxCoxTransformer() 学习了变换的最佳 lambda 值。我们可以如下检查这些值：

boxcox.lambda_dict_

我们看到了以下最优的 lambda 值：

{'LotArea': 0.0028222323212918547, 'GrLivArea': -0.006312580181375803}

现在，我们可以继续并转换数据：

train_t = boxcox.transform(X_train)
test_t = boxcox.transform(X_test)

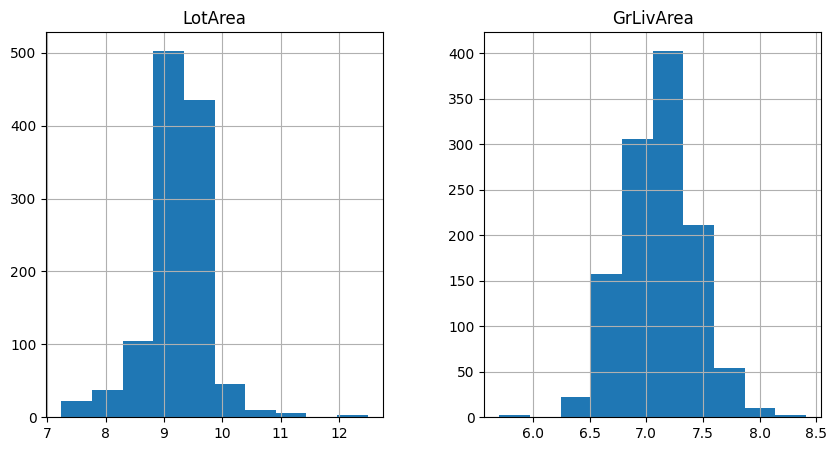
现在让我们通过直方图来检查变换后的变量分布：

train_t[['LotArea', 'GrLivArea']].hist(figsize=(10,5))
plt.show()

在以下直方图中，我们看到变量更好地接近正态分布。

../../_images/nonnormalvars2transformed.png

如果我们想要恢复原始的数据表示，我们也可以这样做：

train_unt = boxcox.inverse_transform(train_t)
test_unt = boxcox.inverse_transform(test_t)

train_unt[['LotArea', 'GrLivArea']].hist(figsize=(10,5))
plt.show()