OutlierTrimmer#
离群点是显著偏离数据集其余部分的数据点,可能表明错误或罕见事件。离群点可以通过扭曲参数估计和降低预测准确性来扭曲机器学习模型的学习过程。为了防止这种情况,如果你怀疑离群点是错误或罕见事件,你可以将其从训练数据中移除。
在本指南中,我们展示了如何使用 OutlierTrimmer() 在 Python 中移除异常值。
去除异常值的第一步是识别这些异常值。异常值可以通过各种统计方法来识别,例如箱线图、z分数、四分位距(IQR)或中位数绝对偏差。此外,使用散点图或直方图对数据进行视觉检查是数据科学中的常见做法,可以帮助检测显著偏离数据集整体模式的观测值。
通过使用所有这些方法,OutlierTrimmer() 可以识别异常值并自动移除它们。因此,我们将从数据分析开始本指南,展示如何通过这些统计方法和箱线图识别异常值,然后我们将使用 OutlierTrimmer() 移除异常值。
识别异常值#
离群值是通常远大于或远小于某个值的数据点,该值决定了分布中大多数值的位置。这些限定数据分布的最小值和最大值可以通过四种方式计算:如果变量呈正态分布,则使用z分数;如果变量偏斜,则使用四分位距接近规则或中位数绝对偏差;或者使用百分位数。
高斯极限或z分数#
如果变量显示正态分布,其大部分值位于均值减去3倍标准差和均值加上3倍标准差之间。因此,我们可以如下确定分布的界限:
右尾 (upper_bound): 均值 + 3* 标准差
左尾(下界):均值 - 3* 标准差
我们可以将那些超出这些界限的数据点视为异常值。
四分位距接近规则#
四分位距接近规则可用于检测在表现出正态分布的变量和偏斜变量中的异常值。使用IQR时,我们将异常值检测为那些位于第25百分位乘以IQR因子之前或第75百分位乘以IQR因子之后的值。这个因子通常是1.5,如果我们想要更严格,则为3。使用IQR方法,限制的计算如下:
IQR 限制:
右尾 (upper_limit): 75% 分位数 + 1.5* IQR
左尾 (下限): 25% 分位数 - 1.5 * IQR
其中 IQR 是四分位距:
IQR = 75th 百分位数 - 25th 百分位数 = 第三四分位数 - 第一四分位数。
超出这些界限的观测值可以被视为极端值。
最大绝对偏差#
像均值和标准差这样的参数会受到异常值的强烈影响。因此,使用一种对异常值稳健的度量标准,如中位数绝对偏差(通常简称为中位数绝对偏差,MAD),来界定正常数据分布,可能是一个更好的解决方案。
当我们使用MAD时,我们确定分布的极限如下:
MAD 限制:
右尾 (upper_limit): 中位数 + 3.29* MAD
左尾 (lower_limit): 中位数 - 3.29* 绝对中位差
MAD 是中位数绝对偏差。换句话说,MAD 是每个观测值与其中位数之间的绝对差异的中位数值。
MAD = 中位数(abs(X-中位数(X)))
百分位数#
确定数据分布界限值的一个更简单的方法是使用百分位数。这样,异常值将是那些位于某个百分位数或分位数之前或之后的值:
右尾:第95百分位
左尾: 第5百分位
这些方法识别出的异常值数量会有所不同。这些方法可以检测异常值,但无法判断它们是真正的异常值还是可靠的数据点。这需要进一步的检查和领域知识。
让我们继续学习如何在Python中移除异常值。
在 Python 中移除异常值#
在这个演示中,我们将识别并从泰坦尼克号数据集中移除异常值。首先,让我们加载数据并将其分为训练集和测试集:
from sklearn.model_selection import train_test_split
from feature_engine.datasets import load_titanic
from feature_engine.outliers import OutlierTrimmer
X, y = load_titanic(
return_X_y_frame=True,
predictors_only=True,
handle_missing=True,
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0,
)
print(X_train.head())
我们在下面看到生成的 pandas 数据框:
pclass sex age sibsp parch fare cabin embarked
501 2 female 13.000000 0 1 19.5000 Missing S
588 2 female 4.000000 1 1 23.0000 Missing S
402 2 female 30.000000 1 0 13.8583 Missing C
1193 3 male 29.881135 0 0 7.7250 Missing Q
686 3 female 22.000000 0 0 7.7250 Missing Q
识别异常值#
现在让我们通过使用箱线图来识别训练集中的潜在极值。
X_train.boxplot(column=['age', 'fare', 'sibsp'])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
在以下箱线图中,我们看到所有三个变量都有显著大于大多数数据分布的数据点。变量年龄也显示了向较低值的异常值。
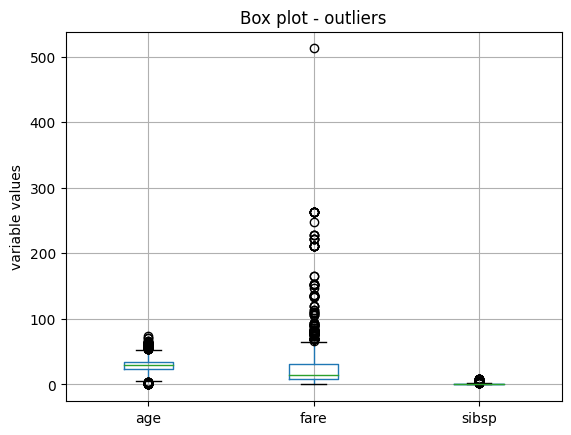
变量具有不同的尺度,因此让我们分别绘制它们以获得更好的可视化效果。首先从绘制变量 fare 的箱线图开始:
X_train.boxplot(column=['fare'])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
我们在以下图像中看到箱线图:
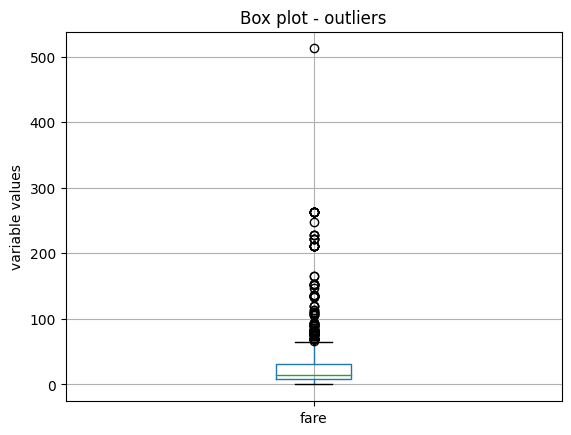
接下来,我们绘制变量年龄:
X_train.boxplot(column=['age'])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
我们在以下图像中看到箱线图:
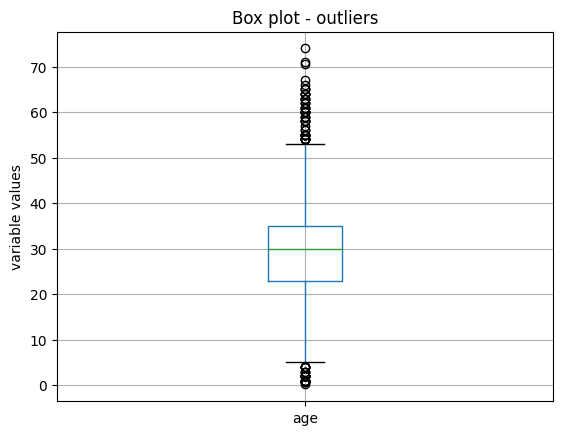
最后,我们对变量 sibsp 进行箱线图绘制:
X_train.boxplot(column=['sibsp'])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
我们在以下图像中看到箱线图和异常值:
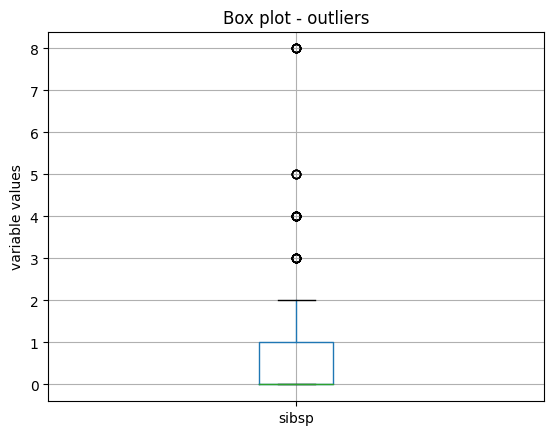
异常值移除#
现在,我们将使用 OutlierTrimmer() 来移除异常值。我们将首先使用 IQR 作为异常值检测方法。
IQR#
我们只想移除分布右侧的异常值(参数 tail)。我们希望使用变量的第75百分位数(参数 capping_method)加上1.5倍的四分位距(参数 fold)来确定最大值。并且我们只想在2个变量中设定异常值的上限,我们在列表中指定了这些变量。
ot = OutlierTrimmer(capping_method='iqr',
tail='right',
fold=1.5,
variables=['sibsp', 'fare'],
)
ot.fit(X_train)
使用 fit() 方法,OutlierTrimmer() 会找到应该对变量进行封顶的值。这些值存储在其一个属性中:
ot.right_tail_caps_
{'sibsp': 2.5, 'fare': 66.34379999999999}
我们现在可以继续并移除异常值:
train_t = ot.transform(X_train)
test_t = ot.transform(X_test)
我们可以比较原始数据集和转换后数据集的大小,以检查异常值是否已被移除:
X_train.shape, train_t.shape
我们看到转换后的数据集包含较少的行:
((916, 8), (764, 8))
如果我们现在评估转换后的数据集中变量的最大值,它们应该 <= 在属性 right_tail_caps_ 中观察到的值。
train_t[['fare', 'age']].max()
fare 65.0
age 53.0
dtype: float64
最后,我们可以检查转换变量的箱线图,以证实它们分布的效果。
train_t.boxplot(column=['sibsp', "fare"])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
我们看到箱线图,sibsp 不再有异常值,但由于 fare 非常偏斜,在移除异常值时,IQR 的参数发生变化,我们继续看到异常值:
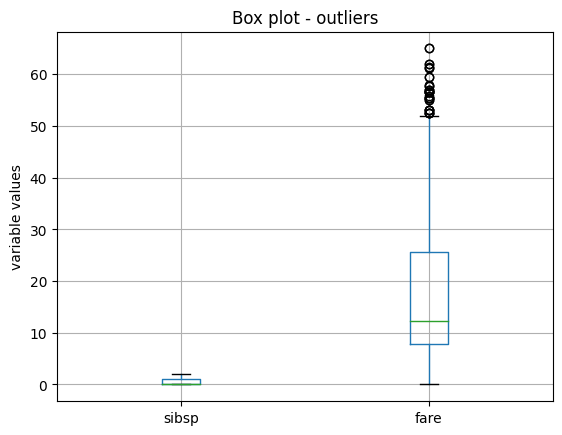
我们稍后会回到这一点,但现在让我们继续展示 OutlierTrimmer() 的功能。
当我们从数据集中移除异常值后,我们需要重新对齐目标变量。我们可以使用 pandas 的 loc 来实现这一点。但 OutlierTrimmer() 可以自动完成如下操作:
train_t, y_train_t = ot.transform_x_y(X_train, y_train)
test_t, y_test_t = ot.transform_x_y(X_test, y_test)
方法 transform_x_y 将从预测数据集中移除异常值,然后对目标变量进行对齐。这意味着,它将从目标中移除那些对应于异常值的行。
我们可以如下验证目标中的尺寸调整:
y_train.shape, y_train_t.shape,
上一个命令返回以下输出:
((916,), (764,))
我们可以按如下方式获取转换后的数据集中特征的名称:
ot.get_feature_names_out()
这将返回以下变量名称:
['pclass', 'sex', 'age', 'sibsp', 'parch', 'fare', 'cabin', 'embarked']
MAD#
我们看到,对于变量票价,IQR 的效果并不理想,因为它的偏斜度过大。因此,让我们改用 MAD 来去除异常值:
ot = OutlierTrimmer(capping_method='mad',
tail='right',
fold=3,
variables=['fare'],
)
ot.fit(X_train)
train_t, y_train_t = ot.transform_x_y(X_train, y_train)
test_t, y_test_t = ot.transform_x_y(X_test, y_test)
train_t.boxplot(column=["fare"])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
在下图中,我们可以看到,经过这种转换后,变量 fare 不再显示异常值:
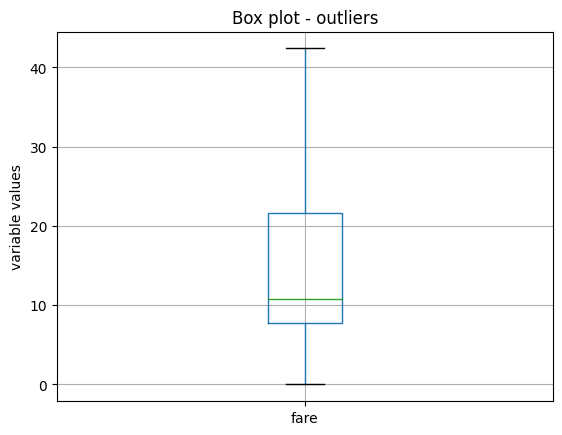
Z-score#
变量 age 在其值范围内分布更为均匀,因此我们使用 z-score 或高斯近似来检测异常值。我们在箱线图中看到它在两端都有异常值,因此我们将对分布的两端进行限制:
ot_age = OutlierTrimmer(capping_method='gaussian',
tail="both",
fold=3,
variables=['age'],
)
ot_age.fit(X_train)
让我们检查超出这些值的数据点将被视为异常值的最大值:
ot_age.right_tail_caps_
{'age': 67.73951212364803}
以及低于此值的数据点将被视为异常值:
ot_age.left_tail_caps_
{'age': -7.410476010820627}
最小值没有意义,因为年龄不能为负。因此,我们将尝试用百分位数来限制这个变量。
百分位数#
我们将年龄限制在底部5%和顶部95%百分位数:
ot = OutlierTrimmer(capping_method='mad',
tail='right',
fold=0.05,
variables=['fare'],
)
ot.fit(X_train)
让我们检查超出这些值的数据点将被视为异常值的最大值:
ot_age.right_tail_caps_
{'age': 54.0}
以及低于此值的数据点将被视为异常值:
ot_age.left_tail_caps_
{'age': 9.0}
让我们转换数据集和目标:
train_t, y_train_t = ot_age.transform_x_y(X_train, y_train)
test_t, y_test_t = ot_age.transform_x_y(X_test, y_test)
并绘制结果变量:
train_t.boxplot(column=['age'])
plt.title("Box plot - outliers")
plt.ylabel("variable values")
plt.show()
在下图中,我们可以看到,经过这种转换后,变量年龄在其较高值处仍然显示一些异常值,因此我们应该对百分位数更加严格,或者使用MAD:
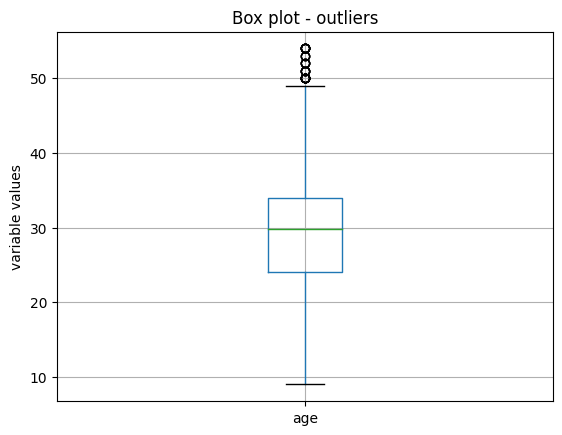
管道#
The OutlierTrimmer() 从预测数据集中移除观测值。如果我们想在 Pipeline 中使用这个转换器,我们不能使用 Scikit-learn 的 pipeline,因为它不能重新调整目标。但我们可以使用 Feature-engine 的 pipeline 来代替。
让我们首先创建一个去除异常值然后编码分类变量的管道:
from feature_engine.encoding import OneHotEncoder
from feature_engine.pipeline import Pipeline
pipe = Pipeline(
[
("outliers", ot),
("enc", OneHotEncoder()),
]
)
pipe.fit(X_train, y_train)
transform 方法将仅对包含预测变量的数据集进行转换,就像 scikit-learn 的管道一样:
train_t = pipe.transform(X_train)
X_train.shape, train_t.shape
我们在这里看到调整后的数据大小与原始大小的比较:
((916, 8), (736, 76))
Feature-engine 的管道也可以调整目标:
train_t, y_train_t = pipe.transform_x_y(X_train, y_train)
y_train.shape, y_train_t.shape
我们在这里看到调整后的数据大小与原始大小的比较:
((916,), (736,))
总结一下,让我们在管道中添加一个机器学习算法。我们将使用逻辑回归来预测生存:
from sklearn.linear_model import LogisticRegression
pipe = Pipeline(
[
("outliers", ot),
("enc", OneHotEncoder()),
("logit", LogisticRegression(random_state=10)),
]
)
pipe.fit(X_train, y_train)
现在,我们可以预测生存:
preds = pipe.predict(X_train)
preds[0:10]
我们看到以下输出:
array([1, 1, 1, 0, 1, 0, 1, 1, 0, 1], dtype=int64)
我们可以获得生存概率:
preds = pipe.predict_proba(X_train)
preds[0:10]
我们看到以下输出:
array([[0.13027536, 0.86972464],
[0.14982143, 0.85017857],
[0.2783799 , 0.7216201 ],
[0.86907159, 0.13092841],
[0.31794531, 0.68205469],
[0.86905145, 0.13094855],
[0.1396715 , 0.8603285 ],
[0.48403632, 0.51596368],
[0.6299007 , 0.3700993 ],
[0.49712853, 0.50287147]])
我们可以获得测试集上预测的准确性:
pipe.score(X_test, y_test)
这返回了以下准确率:
0.7823343848580442
我们可以在转换后获取特征的名称:
pipe[:-1].get_feature_names_out()
这将返回以下名称:
['pclass',
'age',
'sibsp',
'parch',
'fare',
'sex_female',
'sex_male',
'cabin_Missing',
...
最后,我们可以如下获取转换后的数据集和目标:
X_test_t, y_test_t = pipe[:-1].transform_x_y(X_test, y_test)
X_test.shape, X_test_t.shape
我们在这里看到结果的大小:
((393, 8), (317, 76))
设置严格性(参数 fold)#
默认情况下,OutlierTrimmer() 会根据所选的 capping_method 自动确定参数 fold。该参数决定了标准差、四分位距(IQR)或中位数绝对偏差(MAD)的乘数,或者设置变量的上限百分位数。
折叠的默认值如下:
‘gaussian’:
fold设置为 3.0;‘iqr’:
fold设置为 1.5;‘mad’:
fold设置为 3.29;‘percentiles’:
fold设置为 0.05。
您可以手动调整折叠值,以使异常检测过程更加或更少保守,从而自定义异常值修剪的程度。
教程、书籍和课程#
在下面的Jupyter笔记本中,在我们的配套Github仓库中,您将找到更多使用 OutlierTrimmer() 的示例。
关于此功能及其他特征工程方法的教程,请查看我们的在线课程:

机器学习的特征工程#
或者阅读我们的书:

Python 特征工程手册#
我们的书籍和课程都适合初学者和更高级的数据科学家。通过购买它们,您正在支持 Feature-engine 的主要开发者 Sole。
