EqualFrequencyDiscretiser#
等频离散化包括将连续属性划分为等频的区间。这些区间包含大致相同数量的观测值,边界设定在由所需区间数量决定的特定分位数值处。
等频离散化确保数据点在值范围内均匀分布,增强了对偏斜数据和异常值的处理。
离散化是数据科学中常用的数据预处理技术。它也被称为数据分箱(或简称为“分箱”)。
优势与局限#
等频离散化有一些优点和缺点:
优势#
等频分箱的一些优点:
算法效率: 通过提供数据集的简化表示,增强了数据挖掘和机器学习算法的性能。
异常值管理: 通过将异常值分组到极端区间,有效减轻其影响。
数据平滑: 有助于平滑数据,减少噪声,并提高模型的泛化能力。
改进的值分布: 在值范围内返回均匀的值分布。
等频离散化改善了数据分布,优化了数值的分布。这对于具有偏斜分布的数据集特别有益(参见Python示例代码)。
限制#
另一方面,等频分箱可能会通过将数据聚合到更广泛的类别中而导致信息丢失。如果同一箱中的数据对目标有预测信息,这一点尤其令人担忧。
让我们考虑使用决策树模型的二分类任务。一个包含高比例目标类别混合的箱子可能会在此场景中影响模型的性能。
EqualFrequencyDiscretiser#
Feature-engine 的 EqualFrequencyDiscretiser 对数值变量应用等频离散化。它在底层使用 pandas.qcut() 函数来确定区间限制。
你可以通过在设置转换器时传递变量名称的列表来指定要离散化的变量。或者,EqualFrequencyDiscretiser 将自动推断数据类型以计算所有数值变量的区间限制。
最佳区间数量: 使用 EqualFrequencyDiscretiser 时,用户定义了箱的数量。如果变量高度偏斜或不连续,可能需要更小的区间。
与 scikit-learn 的集成: EqualFrequencyDiscretiser 以及所有其他 feature-engine 转换器都能无缝集成到 scikit-learn 的 管道 中。
Python 代码示例#
在本节中,我们将展示 EqualFrequencyDiscretiser 的主要功能。
加载数据集#
在这个例子中,我们将使用 Ames 房价数据集。首先,让我们加载数据集并将其分为训练集和测试集:
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from feature_engine.discretisation import EqualFrequencyDiscretiser
# Load dataset
X, y = fetch_openml(name='house_prices', version=1, return_X_y=True, as_frame=True)
X.set_index('Id', inplace=True)
# Separate into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
等频离散化#
在这个例子中,让我们将两个变量 LotArea 和 GrLivArea 离散化为大约相等观测数量的 10 个区间。
# List the target numeric variables to be transformed
TARGET_NUMERIC_FEATURES= ['LotArea','GrLivArea']
# Set up the discretization transformer
disc = EqualFrequencyDiscretiser(q=10, variables=TARGET_NUMERIC_FEATURES)
# Fit the transformer
disc.fit(X_train)
请注意,如果我们不指定变量(默认=`None`),EqualFrequencyDiscretiser 将自动推断数据类型以计算所有数值变量的区间限制。
通过 fit() 方法,离散器学习了分箱边界并将它们保存到一个字典中,这样我们就可以使用它们来转换未见过的数据:
# Learned limits for each variable
disc.binner_dict_
{'LotArea': [-inf,
5000.0,
7105.6,
8099.200000000003,
8874.0,
9600.0,
10318.400000000001,
11173.5,
12208.2,
14570.699999999999,
inf],
'GrLivArea': [-inf,
918.5,
1080.4,
1218.0,
1348.4,
1476.5,
1601.6000000000001,
1717.6999999999998,
1893.0000000000005,
2166.3999999999996,
inf]}
请注意,下限和上限分别设置为 -inf 和 inf。这种行为确保了转换器能够将小于训练集中的最小值或大于训练集中的最大值的值分配到极端的区间。
EqualFrequencyDiscretiser 在存在缺失值的情况下将无法工作。因此,我们应该在拟合转换器之前移除或填补缺失值。
# Transform the data
train_t = disc.transform(X_train)
test_t = disc.transform(X_test)
让我们可视化原始数据和转换后的数据的前几行:
# Raw data
print(X_train[TARGET_NUMERIC_FEATURES].head())
这里我们看到原始变量:
LotArea GrLivArea
Id
136 10400 1682
1453 3675 1072
763 8640 1547
933 11670 1905
436 10667 1661
# Transformed data
print(train_t[TARGET_NUMERIC_FEATURES].head())
在这里,我们观察离散化后的变量:
LotArea GrLivArea
Id
136 6 6
1453 0 1
763 3 5
933 7 8
436 6 6
转换后的数据现在包含与有序计算桶相对应的离散值(0 为第一个,q-1 为最后一个)。
现在,让我们用直方图可视化等宽区间的图,并用等频离散器可视化转换后的数据:
# Instantiate a figure with two axes
fig, axes = plt.subplots(ncols=2, figsize=(10,5))
# Plot raw distribution
X_train['GrLivArea'].plot.hist(bins=disc.q, ax=axes[0])
axes[0].set_title('Raw data with equal width binning')
axes[0].set_xlabel('GrLivArea')
# Plot transformed distribution
train_t['GrLivArea'].value_counts().sort_index().plot.bar(ax=axes[1])
axes[1].set_title('Transformed data with equal frequency binning')
plt.tight_layout(w_pad=2)
plt.show()
正如我们在下图中看到的,区间包含大约相同数量的观测值:
最后,由于 return_object 参数的默认值为 False,转换器输出整数变量:
train_t[TARGET_NUMERIC_FEATURES].dtypes
LotArea int64
GrLivArea int64
dtype: object
返回变量作为对象#
Feature-engine 中的分类编码器默认设计为处理对象类型的变量。因此,为了进一步使用 Feature-engine 对离散化输出进行编码,我们可以设置 return_object=True。这将返回转换后的变量作为对象。
假设我们想要获得变量与目标之间的单调关系。我们可以通过将 return_object 设置为 True 来无缝实现这一点。关于如何使用此功能的教程可在此处找到 这里。
返回 bin 边界#
如果我们想输出区间限制而不是整数,我们可以将 return_boundaries 设置为 True:
# Set up the discretization transformer
disc = EqualFrequencyDiscretiser(
q=10,
variables=TARGET_NUMERIC_FEATURES,
return_boundaries=True)
# Fit the transformer
disc.fit(X_train)
# Transform test set & visualize limit
test_t = disc.transform(X_test)
# Visualize output (boundaries)
print(test_t[TARGET_NUMERIC_FEATURES].head())
转换后的变量现在在输出中显示了区间限制。我们可以立即看到这些区间的箱宽是不同的。换句话说,它们的宽度并不相同,这与我们看到的 等宽离散化 相反。
与离散化为整数的变量不同,这些变量不能用于训练机器学习模型;然而,它们在这种格式下仍然对数据分析非常有帮助,并且可以发送到任何 Feature-engine 编码器进行进一步处理。
LotArea GrLivArea
Id
893 (8099.2, 8874.0] (918.5, 1080.4]
1106 (12208.2, 14570.7] (2166.4, inf]
414 (8874.0, 9600.0] (918.5, 1080.4]
523 (-inf, 5000.0] (1601.6, 1717.7]
1037 (12208.2, 14570.7] (1601.6, 1717.7]
分箱偏斜数据#
现在让我们展示对偏斜变量进行等频离散化的好处。我们将首先导入库和类:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from feature_engine.discretisation import EqualFrequencyDiscretiser
现在,我们将创建一个带有正态分布变量和另一个偏斜变量的玩具数据集:
# Set seed for reproducibility
np.random.seed(42)
# Generate a normally distributed data
normal_data = np.random.normal(loc=0, scale=1, size=1000)
# Generate a right-skewed data using exponential distribution
skewed_data = np.random.exponential(scale=1, size=1000)
# Create dataframe with simulated data
X = pd.DataFrame({'feature1': normal_data, 'feature2': skewed_data})
让我们将两个变量离散化为5个等频箱:
# Instantiate discretizer
disc = EqualFrequencyDiscretiser(q=5)
# Transform simulated data
X_transformed = disc.fit_transform(X)
让我们绘制原始分布和经过离散化后的分布,针对那些原本呈正态分布的变量:
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].hist(X.feature1, bins=disc.q)
axes[0].set(xlabel='feature1', ylabel='count', title='Raw data')
X_transformed.feature1.value_counts().sort_index().plot.bar(ax=axes[1])
axes[1].set_title('Transformed data')
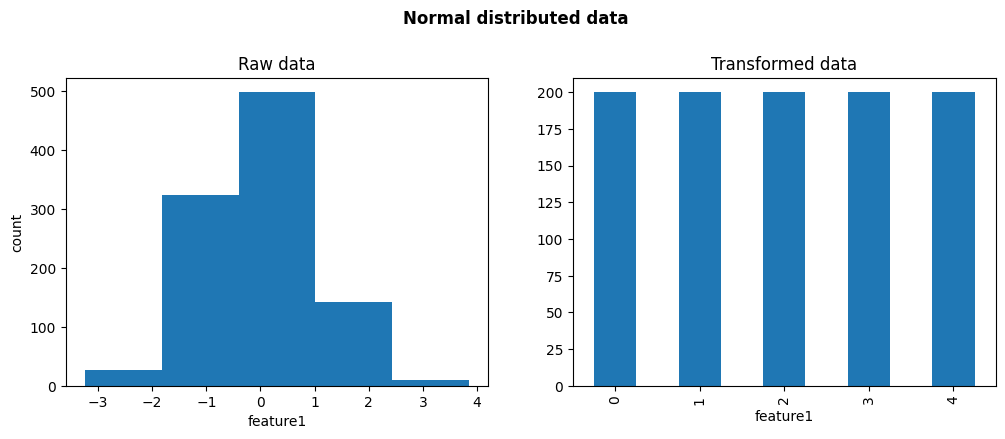
plt.suptitle('Normal distributed data', weight='bold', size='large', y=1.05)
plt.show()
在下图中,我们看到在离散化之后,值在整个值范围内均匀分布,因此,该变量不再看起来是正态分布的。

现在让我们绘制原始分布和离散化后的分布,针对偏斜的变量:
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].hist(X.feature2, bins=disc.q)
axes[0].set(xlabel='feature2', ylabel='count', title='Raw data')
X_transformed.feature2.value_counts().sort_index().plot.bar(ax=axes[1])
axes[1].set_title('Transformed data')
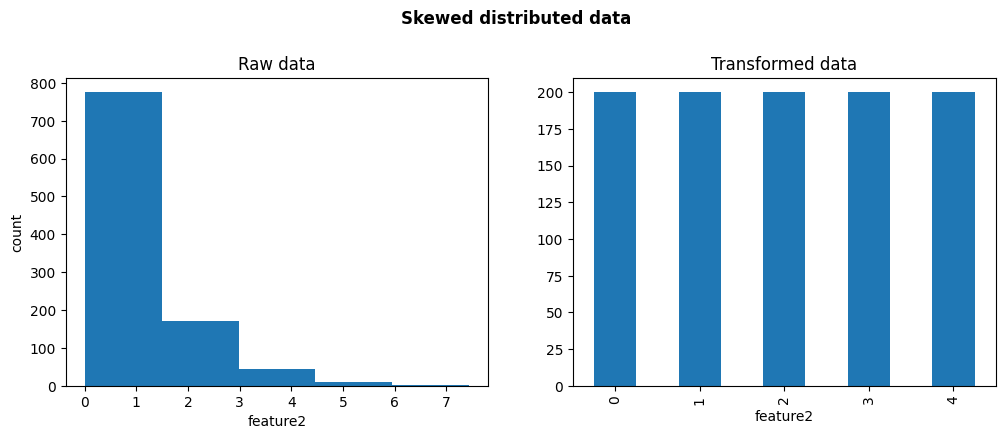
plt.suptitle('Skewed distributed data', weight='bold', size='large', y=1.05)
plt.show()
在下图中,我们可以看到在离散化之后,值在整个值范围内均匀分布。