生物力学建模简介

sympy.physics.biomechanics provides features to enhance models created using sympy.physics.mechanics with force producing elements that model muscles and tendons. In this tutorial, we will introduce the features of this module.

The initial primary purpose of the biomechanics package is to introduce tools for modeling the forces produced by Hill-type muscle models. These models generate forces applied to the skeletal structure of an organism based on the contraction state of the muscle coupled with the passive stretch of tendons. In this tutorial, we introduce the elements that make up a musculotendon model and then demonstrate it in operation with a specific implementation, the MusculotendonDeGroote2016 model.

加载

sympy.physics.mechanics includes two types of loads: Force and Torque. Forces represent bound vector quantities that act directed along a line of action and torques are unbound vectors which represent the resulting torque of a couple from a set of forces.

一个非常常见的力模型是并联的线性弹簧和线性阻尼器。作用在质量为 \(m\) 的粒子上的力，其1D运动由广义坐标 \(x(t)\) 描述，且具有线性弹簧和阻尼系数 \(k\) 和 \(c\)，其运动方程为：

\[m \ddot{x} = \sum F = -kx - c\dot{x}\]

在 SymPy 中，我们可以这样表述作用在粒子 \(P\) 上的力，该粒子在参考系 \(N\) 中有运动，并且相对于固定在 \(N\) 中的点 \(O\) 有位置：

>>> import sympy as sm
>>> import sympy.physics.mechanics as me

>>> k, c = sm.symbols('k, c', real=True, nonnegative=True)
>>> x = me.dynamicsymbols('x', real=True)

>>> N = me.ReferenceFrame('N')
>>> O, P = me.Point('O'), me.Point('P')

>>> P.set_pos(O, x*N.x)
>>> P.set_vel(N, x.diff()*N.x)

>>> force_on_P = me.Force(P, -k*P.pos_from(O) - c*P.vel(N))
>>> force_on_P
(P, (-c*Derivative(x(t), t) - k*x(t))*N.x)

并且会有一个大小相等、方向相反的力作用在 \(O\) 上：

>>> force_on_O = me.Force(O, k*P.pos_from(O) + c*P.vel(N))
>>> force_on_O
(O, (c*Derivative(x(t), t) + k*x(t))*N.x)

一个肌肉和肌腱对一组刚体施加的力将是本教程中进一步开发的肌腱模型中的主要输出。

路径

Muscles and their associated tendons wrap around the moving skeletal system, as well as other muscles and organs. This imposes the challenge of determining the lines of action of the forces that the muscle and tendon produce on the skeleton and organs it touches. We have introduced the pathway module to help manage the specification of the geometric relationships to the forces’ lines of action.

The spring-damper example above has the simplest line of action definition so we can use a LinearPathway to establish that line of action. First provide the two endpoints where the force will have equal and opposite application to and the distance between the points and the relative speed between the two points are calculated by the pathway with length and extension_velocity. Note that a positive speed implies the points are moving away from each other. Also note that the formulation handles the case where \(x\) is positive or negative.

>>> lpathway = me.LinearPathway(O, P)
>>> lpathway
LinearPathway(O, P)
>>> lpathway.length
Abs(x(t))
>>> lpathway.extension_velocity
sign(x(t))*Derivative(x(t), t)

The to_loads method then takes the magnitude of a force with a sign convention that positive magnitudes push the two points away from each other and returns a list of all forces acting on the two points.

>>> import pprint
>>> pprint.pprint(lpathway.to_loads(-k*x - k*x.diff()))
[Force(point=O, force=(k*x(t) + k*Derivative(x(t), t))*x(t)/Abs(x(t))*N.x),
 Force(point=P, force=(-k*x(t) - k*Derivative(x(t), t))*x(t)/Abs(x(t))*N.x)]

Pathways can be constructed with any arbitrary geometry and any number of interconnected particles and rigid bodies. An example, a more complicated pathway is an ObstacleSetPathway. You can specify any number of intermediate points between the two pathway endpoints which the actuation path of the forces will follow along. For example, if we introduce two points fixed in \(N\) then the force will act along a set of linear segments connecting \(O\) to \(Q\) to \(R\) then to \(P\). Each of the four points will experience resultant forces. For simplicity we show the effect of only the spring force.

>>> Q, R = me.Point('Q'), me.Point('R')
>>> Q.set_pos(O, 1*N.y)
>>> R.set_pos(O, 1*N.x + 1*N.y)
>>> opathway = me.ObstacleSetPathway(O, Q, R, P)
>>> opathway.length
sqrt((x(t) - 1)**2 + 1) + 2
>>> opathway.extension_velocity
(x(t) - 1)*Derivative(x(t), t)/sqrt((x(t) - 1)**2 + 1)
>>> pprint.pprint(opathway.to_loads(-k*opathway.length))
[Force(point=O, force=k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.y),
 Force(point=Q, force=- k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.y),
 Force(point=Q, force=k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.x),
 Force(point=R, force=- k*(sqrt((x(t) - 1)**2 + 1) + 2)*N.x),
 Force(point=R, force=k*(sqrt((x(t) - 1)**2 + 1) + 2)*(x(t) - 1)/sqrt((x(t) - 1)**2 + 1)*N.x - k*(sqrt((x(t) - 1)**2 + 1) + 2)/sqrt((x(t) - 1)**2 + 1)*N.y),
 Force(point=P, force=- k*(sqrt((x(t) - 1)**2 + 1) + 2)*(x(t) - 1)/sqrt((x(t) - 1)**2 + 1)*N.x + k*(sqrt((x(t) - 1)**2 + 1) + 2)/sqrt((x(t) - 1)**2 + 1)*N.y)]

如果你设定 \(x=1\)，那么可以更容易地看出力的集合是正确的：

>>> for load in opathway.to_loads(-k*opathway.length):
...     pprint.pprint(me.Force(load[0], load[1].subs({x: 1})))
Force(point=O, force=3*k*N.y)
Force(point=Q, force=- 3*k*N.y)
Force(point=Q, force=3*k*N.x)
Force(point=R, force=- 3*k*N.x)
Force(point=R, force=- 3*k*N.y)
Force(point=P, force=3*k*N.y)

You can create your own pathways by sub-classing PathwayBase.

包装几何体

It is common for muscles to wrap over bones, tissue, or organs. We have introduced wrapping geometries and associated wrapping pathways to help manage their complexities. For example, if two pathway endpoints lie on the surface of a cylinder the forces act along lines that are tangent to the geodesic connecting the two points at the endpoints. The WrappingCylinder object calculates the complex geometry for the pathway. A WrappingPathway then uses the geometry to construct the forces. A spring force along this pathway is constructed below:

>>> r = sm.symbols('r', real=True, nonegative=True)
>>> theta = me.dynamicsymbols('theta', real=True)
>>> O, P, Q = sm.symbols('O, P, Q', cls=me.Point)
>>> A = me.ReferenceFrame('A')

>>> A.orient_axis(N, theta, N.z)

>>> P.set_pos(O, r*N.x)
>>> Q.set_pos(O, N.z + r*A.x)

>>> cyl = me.WrappingCylinder(r, O, N.z)
>>> wpathway = me.WrappingPathway(P, Q, cyl)
>>> pprint.pprint(wpathway.to_loads(-k*wpathway.length))
[Force(point=P, force=- k*r*Abs(theta(t))*N.y - k*N.z),
 Force(point=Q, force=k*N.z + k*r*Abs(theta(t))*A.y),
 Force(point=O, force=k*r*Abs(theta(t))*N.y - k*r*Abs(theta(t))*A.y)]

执行器

Models of multibody systems commonly have time varying inputs in the form of the magnitudes of forces or torques. In many cases, these specified inputs may be derived from the state of the system or even from the output of another dynamic system. The actuator module includes classes to help manage the creation of such models of force and torque inputs. An actuator is intended to represent a real physical component. For example, the spring-damper force from above can be created by sub-classing ActuatorBase and implementing a method that generates the loads associated with that spring-damper actuator.

>>> N = me.ReferenceFrame('N')
>>> O, P = me.Point('O'), me.Point('P')
>>> P.set_pos(O, x*N.x)

>>> class SpringDamper(me.ActuatorBase):
...
...     # positive x spring is in tension
...     # negative x spring is in compression
...     def __init__(self, P1, P2, spring_constant, damper_constant):
...         self.P1 = P1
...         self.P2 = P2
...         self.k = spring_constant
...         self.c = damper_constant
...
...     def to_loads(self):
...         x = self.P2.pos_from(self.P1).magnitude()
...         v = x.diff(me.dynamicsymbols._t)
...         dir_vec = self.P2.pos_from(self.P1).normalize()
...         force_P1 = me.Force(self.P1,
...                             self.k*x*dir_vec + self.c*v*dir_vec)
...         force_P2 = me.Force(self.P2,
...                             -self.k*x*dir_vec - self.c*v*dir_vec)
...         return [force_P1, force_P2]
...

>>> spring_damper = SpringDamper(O, P, k, c)
>>> pprint.pprint(spring_damper.to_loads())
[Force(point=O, force=(c*x(t)*sign(x(t))*Derivative(x(t), t)/Abs(x(t)) + k*x(t))*N.x),
 Force(point=P, force=(-c*x(t)*sign(x(t))*Derivative(x(t), t)/Abs(x(t)) - k*x(t))*N.x)]

There is also a ForceActuator that allows seamless integration with pathway objects. You only need to set the .force attribute in initialization in the sub-class.

>>> class SpringDamper(me.ForceActuator):
...
...     # positive x spring is in tension
...     # negative x spring is in compression
...     def __init__(self, pathway, spring_constant, damper_constant):
...         self.pathway = pathway
...         self.force = (-spring_constant*pathway.length -
...                       damper_constant*pathway.extension_velocity)
...
>>> spring_damper2 = SpringDamper(lpathway, k, c)
>>> pprint.pprint(spring_damper2.to_loads())
[Force(point=O, force=(c*sign(x(t))*Derivative(x(t), t) + k*Abs(x(t)))*x(t)/Abs(x(t))*N.x),
 Force(point=P, force=(-c*sign(x(t))*Derivative(x(t), t) - k*Abs(x(t)))*x(t)/Abs(x(t))*N.x)]

这使得向其他路径应用弹簧-阻尼力变得容易，例如：

>>> spring_damper3 = SpringDamper(wpathway, k, c)
>>> pprint.pprint(spring_damper3.to_loads())
[Force(point=P, force=r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*N.y + (-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))/sqrt(r**2*theta(t)**2 + 1)*N.z),
 Force(point=Q, force=- (-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))/sqrt(r**2*theta(t)**2 + 1)*N.z - r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*A.y),
 Force(point=O, force=- r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*N.y + r*(-c*r**2*theta(t)*Derivative(theta(t), t)/sqrt(r**2*theta(t)**2 + 1) - k*sqrt(r**2*theta(t)**2 + 1))*Abs(theta(t))/sqrt(r**2*theta(t)**2 + 1)*A.y)]

激活动力学

肌腱模型在激活时能够产生主动收缩力。生物学上，当 :math:` extrm{Ca}^{2+}` 离子在肌肉纤维中以足够高的浓度存在时，肌肉开始自主收缩。这种自主收缩的状态称为“激活”。在生物力学模型中，它通常用符号 \(a(t)\) 表示，该符号被视为范围在 \([0, 1]\) 内的归一化量。

生物体并不直接控制其肌肉中这些 \(\textrm{Ca}^{2+}\) 离子的浓度，而是其神经系统（由大脑控制）向肌肉发送电信号，导致 \(\textrm{Ca}^{2+}\) 离子被释放。这些离子扩散并在整个肌肉中增加浓度，从而导致激活。传递到肌肉以刺激收缩的电信号称为“兴奋”。在生物力学模型中，它通常用符号 \(e(t)\) 表示，该符号也被视为范围在 \([0, 1]\) 内的归一化量。

The relationship between the excitation input and the activation state is known as activation dynamics. Because activation dynamics are so common in biomechanical models, SymPy provides the activation module, which contains implementations for some common models of activation dynamics. These are zeroth-order activation dynamics and first-order activation dynamics based on the equations from the paper by [DeGroote2016]. Below we will work through manually implementing these models and then show how these relate to the classes provided by SymPy.

零阶

最简单的激活动力学模型是假设 :math:` extrm{Ca}^{2+}` 离子的扩散是瞬时的。从数学上讲，这给我们提供了 \(a(t) = e(t)\)，一个零阶常微分方程。

>>> e = me.dynamicsymbols('e')
>>> e
e(t)
>>> a = e
>>> a
e(t)

Alternatively, you could give \(a(t)\) its own dynamicsymbols and use a substitution to replace this with \(e(t)\) in any equation.

>>> a = me.dynamicsymbols('a')
>>> zeroth_order_activation = {a: e}
>>> a.subs(zeroth_order_activation)
e(t)

SymPy provides the class ZerothOrderActivation in the activation module. This class must be instantiated with a single argument, name, which associates a name with the instance. This name should be unique per instance.

>>> from sympy.physics.biomechanics import ZerothOrderActivation
>>> actz = ZerothOrderActivation('zeroth')
>>> actz
ZerothOrderActivation('zeroth')

The argument passed to \(name\) tries to help ensures that the automatically-created dynamicsymbols for \(e(t)\) and \(a(t)\) are unique betweem instances.

>>> actz.excitation
e_zeroth(t)
>>> actz.activation
e_zeroth(t)

ZerothOrderActivation subclasses ActivationBase, which provides a consistent interface for all concrete classes of activation dynamics. This includes a method to inspect the ordinary differential equation(s) associated with the model. As zeroth-order activation dynamics correspond to a zeroth-order ordinary differential equation, this returns an empty column matrix.

>>> actz.rhs()
Matrix(0, 1, [])

一阶

在实践中，:math:` extrm{Ca}^{2+}` 离子的扩散和浓度增加不是瞬时的。在真实的生物肌肉中，兴奋度的阶跃增加将导致激活度的平滑和逐渐增加。[DeGroote2016] 使用一阶常微分方程对此进行建模：

\[\begin{split}\frac{da}{dt} &= \left( \frac{1}{\tau_a \left(1 + 3a(t)\right)} (1 + 2f) + \frac{1 + 3a(t)}{4\tau_d} (1 - 2f) \right) \left(e(t) - a(t) \right) \\ f &= \frac{1}{2} \tanh{\left(b \left(e(t) -a(t)\right)\right)}\end{split}\]

其中 \(\tau_a\) 是激活的时间常数，\(\tau_d\) 是去激活的时间常数，而 \(b\) 是一个平滑系数。

>>> tau_a, tau_d, b = sm.symbols('tau_a, tau_d, b')
>>> f = sm.tanh(b*(e - a))/2
>>> dadt = ((1/(tau_a*(1 + 3*a)))*(1 + 2*f) + ((1 + 3*a)/(4*tau_d))*(1 - 2*f))*(e - a)

这个一阶常微分方程随后可以用于在模拟中根据输入 \(e(t)\) 传播状态 \(a(t)\)。

Like before, SymPy provides the class FirstOrderActivationDeGroote2016 in the activation module. This class is another subclass of ActivationBase and uses the model for first-order activation dynamics from [DeGroote2016] defined above. This class must be instantiated with four arguments: a name, and three sympifiable objects to represent the three constants \(\tau_a\), \(\tau_d\), and \(b\).

>>> from sympy.physics.biomechanics import FirstOrderActivationDeGroote2016
>>> actf = FirstOrderActivationDeGroote2016('first', tau_a, tau_d, b)
>>> actf.excitation
e_first(t)
>>> actf.activation
a_first(t)

一阶常微分方程可以像以前一样访问，但这次返回的是一个长度为1的列向量。

>>> actf.rhs()
Matrix([[((1/2 - tanh(b*(-a_first(t) + e_first(t)))/2)*(3*a_first(t)/2 + 1/2)/tau_d + (tanh(b*(-a_first(t) + e_first(t)))/2 + 1/2)/(tau_a*(3*a_first(t)/2 + 1/2)))*(-a_first(t) + e_first(t))]])

您也可以使用每个常量的建议值来实例化该类。这些值为：\(\tau_a = 0.015\)，\(\tau_d = 0.060\)，以及 \(b = 10.0\)。

>>> actf2 = FirstOrderActivationDeGroote2016.with_defaults('first')
>>> actf2.rhs()
Matrix([[((1/2 - tanh(10.0*a_first(t) - 10.0*e_first(t))/2)/(0.0225*a_first(t) + 0.0075) + 16.6666666666667*(3*a_first(t)/2 + 1/2)*(tanh(10.0*a_first(t) - 10.0*e_first(t))/2 + 1/2))*(-a_first(t) + e_first(t))]])
>>> constants = {tau_a: sm.Float('0.015'), tau_d: sm.Float('0.060'), b: sm.Float('10.0')}
>>> actf.rhs().subs(constants)
Matrix([[(66.6666666666667*(1/2 - tanh(10.0*a_first(t) - 10.0*e_first(t))/2)/(3*a_first(t)/2 + 1/2) + 16.6666666666667*(3*a_first(t)/2 + 1/2)*(tanh(10.0*a_first(t) - 10.0*e_first(t))/2 + 1/2))*(-a_first(t) + e_first(t))]])

自定义

To create your own custom models of activation dynamics, you can subclass ActivationBase and override the abstract methods. The concrete class will then conform to the expected API and integrate automatically with the rest of sympy.physics.mechanics and sympy.physics.biomechanics.

肌肉肌腱曲线

多年来，已经发表了许多不同配置的Hill型肌肉模型，这些模型包含不同组合的串联和并联元素。我们将考虑一个非常常见的模型版本，其中肌腱被建模为与肌肉纤维串联的元素，而肌肉纤维本身则被建模为三个并联元素：一个弹性元素、一个收缩元素和一个阻尼器。

示意图展示了四元素 Hill 型肌肉模型。\(SE\) 是代表肌腱的串联元素，\(CE\) 是收缩元素，\(EE\) 是代表肌纤维弹性的并联元素，\(DE\) 是阻尼器。

这些组件中的每一个通常都有一个描述它的特性曲线。以下小节将描述并实现 [DeGroote2016] 论文中描述的特性曲线。

肌腱力-长度

通常将肌腱建模为刚性（不可伸长）和弹性元件。如果将肌腱视为刚性，则肌腱长度不变，肌肉纤维长度直接随肌腱长度变化而变化。刚性肌腱不会有相关的特征曲线；它本身不具备任何产力能力，只是直接传递肌肉纤维产生的力。

如果肌腱是弹性的，通常将其建模为非线性弹簧。因此，我们得到了第一个特征曲线，即肌腱力-长度曲线，它是肌腱长度归一化的函数：

\[\tilde{l}^T = \frac{l^T}{l^T_{slack}}\]

其中 \(l^T\) 是肌腱长度，而 \(l^T_{slack}\) 是“肌腱松弛长度”，一个表示无应力状态下肌腱长度的常数。特征肌腱曲线是根据“归一化”（或“无量纲”）量来参数化的，例如 :math:` ilde{l}^T`，因为这些曲线普遍适用于所有肌纤维和肌腱。它们的特性可以通过选择不同的常数值来调整，以模拟特定的肌腱。在肌腱力-长度特性的情况下，这是通过调整 \(l^T_{slack}\) 来完成的。该常数值越小，肌腱越硬。

肌腱力-长度曲线的方程 \(fl^T\left(\tilde{l}^T\right)\) 来自 [DeGroote2016] 如下：

\[fl^T\left(\tilde{l}^T\right) = c_0 \exp{c_3 \left( \tilde{l}^T - c_1 \right)} - c_2\]

要在 SymPy 中实现这一点，我们需要一个表示 \(\tilde{l}^T\) 的随时间变化的动态符号和四个表示四个常数的符号。

>>> l_T_tilde = me.dynamicsymbols('l_T_tilde')
>>> c0, c1, c2, c3 = sm.symbols('c0, c1, c2, c3')

>>> fl_T = c0*sm.exp(c3*(l_T_tilde - c1)) - c2
>>> fl_T
c0*exp(c3*(-c1 + l_T_tilde(t))) - c2

或者，我们可以根据 \(l^T\) 和 \(l^T_{slack}\) 来定义这一点。

>>> l_T = me.dynamicsymbols('l_T')
>>> l_T_slack = sm.symbols('l_T_slack')

>>> fl_T = c0*sm.exp(c3*(l_T/l_T_slack - c1)) - c2
>>> fl_T
c0*exp(c3*(-c1 + l_T(t)/l_T_slack)) - c2

The biomechanics module in SymPy provides a class for this exact curve, TendonForceLengthDeGroote2016. It can be instantiated with five arguments. The first argument is \(\tilde{l}^T\), which need not necessarily be a symbol; it could be an expression. The further four arguments are all constants. It is intended that these will be constants, or sympifiable numerical values.

>>> from sympy.physics.biomechanics import TendonForceLengthDeGroote2016

>>> fl_T2 = TendonForceLengthDeGroote2016(l_T/l_T_slack, c0, c1, c2, c3)
>>> fl_T2
TendonForceLengthDeGroote2016(l_T(t)/l_T_slack, c0, c1, c2, c3)

This class is a subclass of Function and so implements usual SymPy methods for substitution, evaluation, differentiation etc. The doit method allows the equation of the curve to be accessed.

>>> fl_T2.doit()
c0*exp(c3*(-c1 + l_T(t)/l_T_slack)) - c2

该类提供了一个替代构造函数，允许它在构建时预填充 [DeGroote2016] 中推荐的常量值。这需要一个参数，同样对应于 \(\tilde{l}^T\)，可以是符号或表达式。

>>> fl_T3 = TendonForceLengthDeGroote2016.with_defaults(l_T/l_T_slack)
>>> fl_T3
TendonForceLengthDeGroote2016(l_T(t)/l_T_slack, 0.2, 0.995, 0.25, 33.93669377311689)

In the above the constants have been replaced with instances of SymPy numeric types like Float.

The TendonForceLengthDeGroote2016 class also supports code generation, so seamlessly integrates with SymPy’s code printers. To visualize this curve, we can use lambdify on an instance of the function, which will create a callable to evaluate it for a given value of \(\tilde{l}^T\). Sensible values for \(\tilde{l}^T\) fall within the range \([0.95, 1.05]\), which we will plot below.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import TendonForceLengthDeGroote2016

>>> l_T_tilde = me.dynamicsymbols('l_T_tilde')
>>> fl_T = TendonForceLengthDeGroote2016.with_defaults(l_T_tilde)
>>> fl_T_callable = sm.lambdify(l_T_tilde, fl_T)
>>> l_T_tilde_num = np.linspace(0.95, 1.05)

>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_T_tilde_num, fl_T_callable(l_T_tilde_num))
>>> _ = ax.set_xlabel('Normalized tendon length')
>>> _ = ax.set_ylabel('Normalized tendon force-length')

(png, hires.png, pdf)

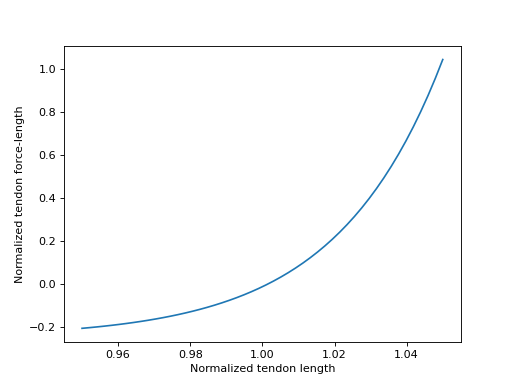
在推导描述具有弹性肌腱模型的肌腱动力学方程时，了解肌腱力-长度特性曲线的反函数可能会有所帮助。在 [DeGroote2016] 中定义的曲线是解析可逆的，这意味着我们可以直接确定 \(\tilde{l}^T = \left[fl^T\left(\tilde{l}^T\right)\right]^{-1}\) 对于给定的 \(fl^T\left(\tilde{l}^T\right)\) 值。

\[\tilde{l}^T = \left[fl^T\left(\tilde{l}^T\right)\right]^{-1} = \frac{\log{\frac{fl^T + c_2}{c_0}}}{c_3} + c_1\]

There is also a class for this in biomechanics, TendonForceLengthInverseDeGroote2016, which behaves identically to TendonForceLengthDeGroote2016. It can be instantiated with five parameters, the first for \(fl^T\) followed by four constants, or by using the alternate constructor with a single argument for \(fl^T\).

>>> from sympy.physics.biomechanics import TendonForceLengthInverseDeGroote2016

>>> fl_T_sym =me.dynamicsymbols('fl_T')
>>> fl_T_inv = TendonForceLengthInverseDeGroote2016(fl_T_sym, c0, c1, c2, c3)
>>> fl_T_inv
TendonForceLengthInverseDeGroote2016(fl_T(t), c0, c1, c2, c3)

>>> fl_T_inv2 = TendonForceLengthInverseDeGroote2016.with_defaults(fl_T_sym)
>>> fl_T_inv2
TendonForceLengthInverseDeGroote2016(fl_T(t), 0.2, 0.995, 0.25, 33.93669377311689)

纤维被动力-长度

用于建模肌肉纤维的第一个元素是纤维被动力-长度。这本质上是一个表示肌肉纤维弹性特性的非线性弹簧。描述该元素的特征曲线是肌肉纤维长度的归一化函数：

\[\tilde{l}^M = \frac{l^M}{l^M_{opt}}\]

其中 \(l^M\) 是肌纤维长度，而 \(l^M_{opt}\) 是“最佳纤维长度”，这是一个常数，表示肌纤维长度在其不产生被动弹性力时的长度（这也是肌纤维长度在其能产生最大主动力时的长度）。与通过调整 \(l^T_{slack}\) 来改变模型肌腱的刚度特性类似，我们可以通过调整 \(l^M_{opt}\) 来改变肌纤维的被动特性；减少 \(l^M_{opt}\) 会使模型肌纤维变得更硬。

纤维被动力-长度曲线的方程 \(fl^M_{pas}\left(\tilde{l}^M\right)\) 来自 [DeGroote2016] 如下：

\[fl^M_{pas} = \frac{\frac{\exp{c_1 \left(\tilde{l^M} - 1\right)}}{c_0} - 1}{\exp{c_1} - 1}\]

与之前类似，要在 SymPy 中实现这一点，我们需要一个表示 :math:` ilde{l}^M` 的随时间变化的动态符号，以及两个表示两个常数的符号。

>>> l_M_tilde = me.dynamicsymbols('l_M_tilde')
>>> c0, c1 = sm.symbols('c0, c1')

>>> fl_M_pas = (sm.exp(c1*(l_M_tilde - 1)/c0) - 1)/(sm.exp(c1) - 1)
>>> fl_M_pas
(exp(c1*(l_M_tilde(t) - 1)/c0) - 1)/(exp(c1) - 1)

或者，我们可以根据 \(l^M\) 和 \(l^M_{opt}\) 来定义这一点。

>>> l_M = me.dynamicsymbols('l_M')
>>> l_M_opt = sm.symbols('l_M_opt')

>>> fl_M_pas2 = (sm.exp(c1*(l_M/l_M_opt - 1)/c0) - 1)/(sm.exp(c1) - 1)
>>> fl_M_pas2
(exp(c1*(-1 + l_M(t)/l_M_opt)/c0) - 1)/(exp(c1) - 1)

Again, the biomechanics module in SymPy provides a class for this exact curve, FiberForceLengthPassiveDeGroote2016. It can be instantiated with three arguments. The first argument is \(\tilde{l}^M\), which need not necessarily be a symbol and can be an expression. The further two arguments are both constants. It is intended that these will be constants, or sympifiable numerical values.

>>> from sympy.physics.biomechanics import FiberForceLengthPassiveDeGroote2016

>>> fl_M_pas2 = FiberForceLengthPassiveDeGroote2016(l_M/l_M_opt, c0, c1)
>>> fl_M_pas2
FiberForceLengthPassiveDeGroote2016(l_M(t)/l_M_opt, c0, c1)
>>> fl_M_pas2.doit()
(exp(c1*(-1 + l_M(t)/l_M_opt)/c0) - 1)/(exp(c1) - 1)

使用替代构造函数，该构造函数接受一个参数用于 \(\tilde{l}^M\)，我们可以创建一个预先填充了 [DeGroote2016] 中推荐的常量值的实例。

>>> fl_M_pas3 = FiberForceLengthPassiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_pas3
FiberForceLengthPassiveDeGroote2016(l_M(t)/l_M_opt, 0.6, 4.0)
>>> fl_M_pas3.doit()
2.37439874427164e-5*exp(6.66666666666667*l_M(t)/l_M_opt) - 0.0186573603637741

合理的 \(\tilde{l}^M\) 值落在范围 \([0.0, 2.0]\) 内，我们将在下面绘制。

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import FiberForceLengthPassiveDeGroote2016

>>> l_M_tilde = me.dynamicsymbols('l_M_tilde')
>>> fl_M_pas = FiberForceLengthPassiveDeGroote2016.with_defaults(l_M_tilde)
>>> fl_M_pas_callable = sm.lambdify(l_M_tilde, fl_M_pas)
>>> l_M_tilde_num = np.linspace(0.0, 2.0)

>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_M_tilde_num, fl_M_pas_callable(l_M_tilde_num))
>>> _ = ax.set_xlabel('Normalized fiber length')
>>> _ = ax.set_ylabel('Normalized fiber passive force-length')

(png, hires.png, pdf)

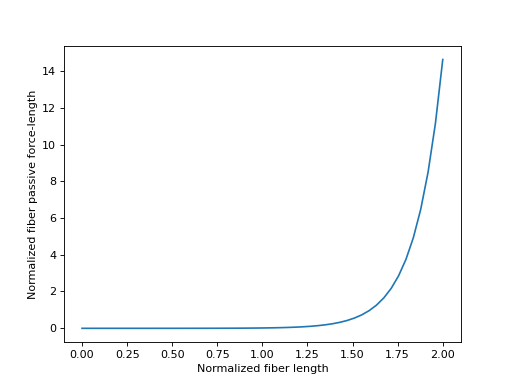
在制定肌腱动力学时，有时需要纤维被动力-长度特性曲线的反函数。来自 [DeGroote2016] 的该曲线的方程再次可以解析地求逆。

\[\tilde{l}^M = \left[fl^M_{pas}\right]^{-1} = \frac{c_0 \log{\left(\exp{c_1} - 1\right)fl^M_{pas} + 1}}{c_1} + 1\]

There is also a class for this in biomechanics, FiberForceLengthPassiveInverseDeGroote2016. It can be instantiated with three parameters, the first for \(fl^M\) followed by a pair of constants, or by using the alternate constructor with a single argument for \(\tilde{l}^M\).

>>> from sympy.physics.biomechanics import FiberForceLengthPassiveInverseDeGroote2016

>>> fl_M_pas_sym =me.dynamicsymbols('fl_M_pas')
>>> fl_M_pas_inv = FiberForceLengthPassiveInverseDeGroote2016(fl_M_pas_sym, c0, c1)
>>> fl_M_pas_inv
FiberForceLengthPassiveInverseDeGroote2016(fl_M_pas(t), c0, c1)

>>> fl_M_pas_inv2 = FiberForceLengthPassiveInverseDeGroote2016.with_defaults(fl_M_pas_sym)
>>> fl_M_pas_inv2
FiberForceLengthPassiveInverseDeGroote2016(fl_M_pas(t), 0.6, 4.0)

纤维主动力-长度

当肌肉被激活时，它会收缩以产生力量。这种现象在肌肉肌腱模型的并联纤维组件中由收缩元件建模。纤维能产生的力量大小是其瞬时长度的函数。描述纤维主动力-长度曲线的特征曲线再次由 \(\tilde{l}^M\) 参数化。这条曲线呈“钟形”。对于非常小和非常大的 \(\tilde{l}^M\) 值，主动纤维力-长度趋向于零。主动纤维力-长度的峰值出现在 \(\tilde{l}^M = l^M_{opt}\) 时，并给出 \(0.0\) 的值。

纤维主动力-长度曲线的方程 \(fl^M_{act}\left(\tilde{l}^M\right)\) 来自 [DeGroote2016] 如下：

\[fl^M_{act}\left(\tilde{l}^M\right) = c_0 \exp{-\frac{1}{2}\left(\frac{\tilde{l}^M - c_1}{\left(c_2 + c_3 \tilde{l}^M\right)}\right)^2} + c_4 \exp{-\frac{1}{2}\left(\frac{\tilde{l}^M - c_5}{\left(c_6 + c_7 \tilde{l}^M\right)}\right)^2} + c_8 \exp{-\frac{1}{2}\left(\frac{\tilde{l}^M - c_9}{\left(c_{10} + c_{11} \tilde{l}^M\right)}\right)^2}\]

要在 SymPy 中实现这一点，我们需要一个表示 \(\tilde{l}^M\) 的随时间变化的动态符号和十二个表示十二个常数的符号。

>>> constants = sm.symbols('c0:12')
>>> c0, c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11 = constants

>>> fl_M_act = (c0*sm.exp(-(((l_M_tilde - c1)/(c2 + c3*l_M_tilde))**2)/2) + c4*sm.exp(-(((l_M_tilde - c5)/(c6 + c7*l_M_tilde))**2)/2) + c8*sm.exp(-(((l_M_tilde - c9)/(c10 + c11*l_M_tilde))**2)/2))
>>> fl_M_act
c0*exp(-(-c1 + l_M_tilde(t))**2/(2*(c2 + c3*l_M_tilde(t))**2)) + c4*exp(-(-c5 + l_M_tilde(t))**2/(2*(c6 + c7*l_M_tilde(t))**2)) + c8*exp(-(-c9 + l_M_tilde(t))**2/(2*(c10 + c11*l_M_tilde(t))**2))

The SymPy-provided class for this exact curve is FiberForceLengthActiveDeGroote2016. It can be instantiated with thirteen arguments. The first argument is \(\tilde{l}^M\), which need not necessarily be a symbol and can be an expression. The further twelve arguments are all constants. It is intended that these will be constants, or sympifiable numerical values.

>>> from sympy.physics.biomechanics import FiberForceLengthActiveDeGroote2016

>>> fl_M_act2 = FiberForceLengthActiveDeGroote2016(l_M/l_M_opt, *constants)
>>> fl_M_act2
FiberForceLengthActiveDeGroote2016(l_M(t)/l_M_opt, c0, c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11)
>>> fl_M_act2.doit()
c0*exp(-(-c1 + l_M(t)/l_M_opt)**2/(2*(c2 + c3*l_M(t)/l_M_opt)**2)) + c4*exp(-(-c5 + l_M(t)/l_M_opt)**2/(2*(c6 + c7*l_M(t)/l_M_opt)**2)) + c8*exp(-(-c9 + l_M(t)/l_M_opt)**2/(2*(c10 + c11*l_M(t)/l_M_opt)**2))

使用替代构造函数，该构造函数接受一个参数用于 \(\tilde{l}^M\)，我们可以创建一个预先填充了 [DeGroote2016] 中推荐的常量值的实例。

>>> fl_M_act3 = FiberForceLengthActiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_act3
FiberForceLengthActiveDeGroote2016(l_M(t)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)
>>> fl_M_act3.doit()
0.1*exp(-3.98991349867535*(-1 + l_M(t)/l_M_opt)**2) + 0.433*exp(-12.5*(-0.717 + l_M(t)/l_M_opt)**2/(-0.1495 + l_M(t)/l_M_opt)**2) + 0.814*exp(-21.4067977442463*(-1 + 0.943396226415094*l_M(t)/l_M_opt)**2/(1 + 0.390740740740741*l_M(t)/l_M_opt)**2)

合理的 \(\tilde{l}^M\) 值落在范围 \([0.0, 2.0]\) 内，我们将在下面绘制。

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import FiberForceLengthActiveDeGroote2016

>>> l_M_tilde = me.dynamicsymbols('l_M_tilde')
>>> fl_M_act = FiberForceLengthActiveDeGroote2016.with_defaults(l_M_tilde)
>>> fl_M_act_callable = sm.lambdify(l_M_tilde, fl_M_act)
>>> l_M_tilde_num = np.linspace(0.0, 2.0)

>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_M_tilde_num, fl_M_act_callable(l_M_tilde_num))
>>> _ = ax.set_xlabel('Normalized fiber length')
>>> _ = ax.set_ylabel('Normalized fiber active force-length')

(png, hires.png, pdf)

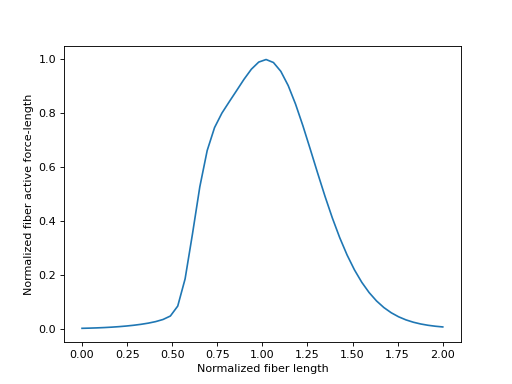
纤维主动力-长度特性曲线不存在反曲线，因为它对每个 \(fl^M_{act}\) 值有多个 :math:` ilde{l}^M` 值。

纤维力-速度

收缩元件产生的力也是其伸长速度的函数。描述收缩元件动力学中依赖速度部分的特征曲线是肌肉纤维伸长速度归一化的函数：

\[\tilde{v}^M = \frac{v^M}{v^M_{max}}\]

其中 \(v^M\) 是肌肉纤维的伸长速度，而 \(v^M_{max}\) 是“最大纤维速度”，一个常数，表示肌肉纤维在向心收缩时无法产生任何收缩力时的速度。\(v^M_{max}\) 通常给定的值为 \(10 l^M_{opt}\)。

纤维力-速度曲线的方程 \(fv^M\left(\tilde{v}^M\right)\) 来自 [DeGroote2016] 如下：

\[fv^M\left(\tilde{v}^M\right) = c_0 \log{\left(c_1 \tilde{v}^M + c_2\right) + \sqrt{\left(c_1 \tilde{v}^M + c_2\right)^2 + 1}} + c_3\]

与之前类似，要在 SymPy 中实现这一点，我们需要一个表示 :math:` ilde{v}^M` 的时变动态符号和四个表示四个常数的符号。

>>> v_M_tilde = me.dynamicsymbols('v_M_tilde')
>>> c0, c1, c2, c3 = sm.symbols('c0, c1, c2, c3')

>>> fv_M = c0*sm.log(c1*v_M_tilde + c2 + sm.sqrt((c1*v_M_tilde + c2)**2 + 1)) + c3
>>> fv_M
c0*log(c1*v_M_tilde(t) + c2 + sqrt((c1*v_M_tilde(t) + c2)**2 + 1)) + c3

或者，我们可以根据 \(v^M\) 和 \(v^M_{max}\) 来定义这一点。

>>> v_M = me.dynamicsymbols('v_M')
>>> v_M_max = sm.symbols('v_M_max')

>>> fv_M_pas2 = c0*sm.log(c1*v_M/v_M_max + c2 + sm.sqrt((c1*v_M/v_M_max + c2)**2 + 1)) + c3
>>> fv_M_pas2
c0*log(c1*v_M(t)/v_M_max + c2 + sqrt((c1*v_M(t)/v_M_max + c2)**2 + 1)) + c3

The SymPy-provided class for this exact curve is FiberForceVelocityDeGroote2016. It can be instantiated with five arguments. The first argument is \(\tilde{v}^M\), which need not necessarily be a symbol and can be an expression. The further four arguments are all constants. It is intended that these will be constants, or sympifiable numerical values.

>>> from sympy.physics.biomechanics import FiberForceVelocityDeGroote2016

>>> fv_M2 = FiberForceVelocityDeGroote2016(v_M/v_M_max, c0, c1, c2, c3)
>>> fv_M2
FiberForceVelocityDeGroote2016(v_M(t)/v_M_max, c0, c1, c2, c3)
>>> fv_M2.doit()
c0*log(c1*v_M(t)/v_M_max + c2 + sqrt((c1*v_M(t)/v_M_max + c2)**2 + 1)) + c3

使用替代构造函数，该构造函数接受一个参数用于 \(\tilde{v}^M\)，我们可以创建一个预先填充了 [DeGroote2016] 中推荐的常量值的实例。

>>> fv_M3 = FiberForceVelocityDeGroote2016.with_defaults(v_M/v_M_max)
>>> fv_M3
FiberForceVelocityDeGroote2016(v_M(t)/v_M_max, -0.318, -8.149, -0.374, 0.886)
>>> fv_M3.doit()
0.886 - 0.318*log(8.149*sqrt((-0.0458952018652595 - v_M(t)/v_M_max)**2 + 0.0150588346410601) - 0.374 - 8.149*v_M(t)/v_M_max)

合理的 \(\tilde{v}^M\) 值落在范围 \([-1.0, 1.0]\) 内，我们将在下面绘制。

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sympy.physics.biomechanics import FiberForceVelocityDeGroote2016

>>> v_M_tilde = me.dynamicsymbols('v_M_tilde')
>>> fv_M = FiberForceVelocityDeGroote2016.with_defaults(v_M_tilde)
>>> fv_M_callable = sm.lambdify(v_M_tilde, fv_M)
>>> v_M_tilde_num = np.linspace(-1.0, 1.0)

>>> fig, ax = plt.subplots()
>>> _ = ax.plot(l_M_tilde_num, fv_M_callable(v_M_tilde_num))
>>> _ = ax.set_xlabel('Normalized fiber velocity')
>>> _ = ax.set_ylabel('Normalized fiber force-velocity')

(png, hires.png, pdf)

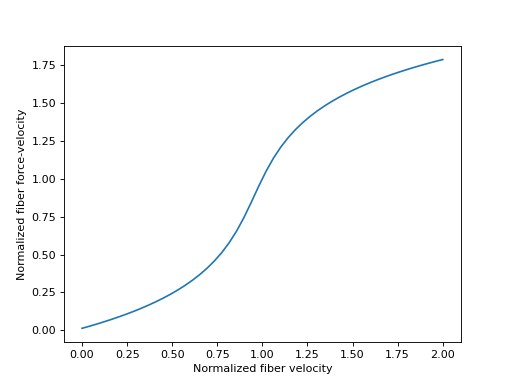
在制定肌腱动力学时，有时需要纤维力-速度特性曲线的反函数。来自 [DeGroote2016] 的该曲线的方程再次可以解析地求逆。

\[\tilde{v}^M = \left[fv^M\right]^{-1} = \frac{\sinh{\frac{fv^M - c_3}{c_0}} - c_2}{c_1}\]

There is also a class for this in biomechanics, FiberForceVelocityInverseDeGroote2016. It can be instantiated with five parameters, the first for \(fv^M\) followed by four constants, or by using the alternate constructor with a single argument for \(\tilde{v}^M\).

>>> from sympy.physics.biomechanics import FiberForceVelocityInverseDeGroote2016

>>> fv_M_sym = me.dynamicsymbols('fv_M')
>>> fv_M_inv = FiberForceVelocityInverseDeGroote2016(fv_M_sym, c0, c1, c2, c3)
>>> fv_M_inv
FiberForceVelocityInverseDeGroote2016(fv_M(t), c0, c1, c2, c3)

>>> fv_M_inv2 = FiberForceVelocityInverseDeGroote2016.with_defaults(fv_M_sym)
>>> fv_M_inv2
FiberForceVelocityInverseDeGroote2016(fv_M(t), -0.318, -8.149, -0.374, 0.886)

光纤阻尼

在肌肉肌腱模型中，最简单的元素可能是纤维阻尼。它没有相关的特征曲线，因为它通常被建模为一个简单的线性阻尼器。我们将使用 \(\beta\) 作为阻尼系数，使得阻尼力可以描述为：

\[f_{damp} = \beta \tilde{v}^M\]

[DeGroote2016] 建议值 \(\beta = 0.1\)。然而，SymPy 默认使用 \(\beta = 10\)。在进行正向模拟或解决最优控制问题时，这种阻尼的增加通常不会显著影响肌肉肌腱动力学，但已被经验性地发现能显著改善方程的数值条件。

肌肉肌腱动力学

刚性腱动力学

刚性肌腱肌肉肌腱动力学实现起来相对简单，因为不可伸长的肌腱允许肌肉纤维长度可以直接用肌腱长度表示。对于不可伸长的肌腱，\(l^T = l^T_{slack}\)，因此，归一化肌腱长度为1，\(\tilde{l}^T = 1\)。利用三角学，肌肉纤维长度可以表示为

\[l^M = \sqrt{\left(l^{MT} - l^T\right)^2 + \left(l^M_{opt} \sin{\alpha_{opt}} \right)^2}\]

其中 \(\alpha_{opt}\) 是“最佳羽状角”，这是肌肉肌腱的另一个常数属性，描述了在 \(l^M = l^M_{opt}\) 时的羽状角（肌肉纤维相对于与肌腱平行方向的角度）。一个常见的简化假设是假设 \(\alpha_{opt} = 0\)，这将上述简化为

\[l^M = \sqrt{\left(l^{MT} - l^T\right)^2 + \left(l^M_{opt}\right)^2}\]

通过 :math:` ilde{l}^M = frac{l^M}{l^M_{opt}}`，肌肉纤维速度可以表示为

\[v^M = v^{MT} \frac{l^{MT} - l^T_{slack}}{l^M}\]

肌肉纤维可以像之前一样归一化，\(\tilde{v}^M = \frac{v^M}{v^M_{max}}\)。使用上述曲线，我们可以将归一化的肌肉纤维力（\(\tilde{F}^M\)）表示为归一化肌腱长度（\(\tilde{l}^T\)）、归一化纤维长度（\(\tilde{l}^M\)）、归一化纤维速度（\(\tilde{v}^M\)）和激活（\(a\)）的函数：

\[\tilde{F}^M = a \cdot fl^M_{act}\left(\tilde{l}^M\right) \cdot fv^M\left(\tilde{v}^M\right) + fl^M_{pas}\left(\tilde{l}^M\right) + \beta \cdot \tilde{v}^M\]

我们引入一个新的常数，\(F^M_{max}\)，即“最大等长力”，它描述了肌肉肌腱在完全激活和等长（\(v^M = 0\)）收缩下能产生的最大力。考虑到羽状角，肌腱力（\(F^T\)），即在肌肉肌腱起点和插入点施加在骨骼上的力，可以表示为：

\[F^T = F^M_{max} \cdot F^M \cdot \sqrt{1 - \sin{\alpha_{opt}}^2}\]

我们可以使用SymPy和上面介绍的肌腱曲线类来描述所有这些。我们需要时间变化的动态符号来表示 \(l^{MT}\)、\(v_{MT}\) 和 \(a\)。我们还需要常量符号来表示 \(l^T_{slack}\)、\(l^M_{opt}\)、\(F^M_{max}\)、\(v^M_{max}\)、\(\alpha_{opt}\) 和 \(\beta\)。

>>> l_MT, v_MT, a = me.dynamicsymbols('l_MT, v_MT, a')
>>> l_T_slack, l_M_opt, F_M_max = sm.symbols('l_T_slack, l_M_opt, F_M_max')
>>> v_M_max, alpha_opt, beta = sm.symbols('v_M_max, alpha_opt, beta')

>>> l_M = sm.sqrt((l_MT - l_T_slack)**2 + (l_M_opt*sm.sin(alpha_opt))**2)
>>> l_M
sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)

>>> v_M = v_MT*(l_MT - l_T_slack)/l_M
>>> v_M
(-l_T_slack + l_MT(t))*v_MT(t)/sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)

>>> fl_M_pas = FiberForceLengthPassiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_pas
FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.6, 4.0)

>>> fl_M_act = FiberForceLengthActiveDeGroote2016.with_defaults(l_M/l_M_opt)
>>> fl_M_act
FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)

>>> fv_M = FiberForceVelocityDeGroote2016.with_defaults(v_M/v_M_max)
>>> fv_M
FiberForceVelocityDeGroote2016((-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)), -0.318, -8.149, -0.374, 0.886)

>>> F_M = a*fl_M_act*fv_M + fl_M_pas + beta*v_M/v_M_max
>>> F_M
beta*(-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)) + a(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.6, 4.0)

>>> F_T = F_M_max*F_M*sm.sqrt(1 - sm.sin(alpha_opt)**2)
>>> F_T
F_M_max*sqrt(1 - sin(alpha_opt)**2)*(beta*(-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)) + a(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + l_MT(t))*v_MT(t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + l_MT(t))**2)/l_M_opt, 0.6, 4.0))

SymPy offers this implementation of rigid tendon dynamics in the MusculotendonDeGroote2016 class, a full demonstration of which is shown below when we will construct a complete simple musculotendon model.

弹性肌腱动力学

弹性肌腱动力学更为复杂，因为由于肌腱长度的变化，我们无法直接用肌腱长度来表示纤维长度。相反，我们必须将肌腱中感受到的力与肌肉纤维产生的力联系起来，确保两者处于平衡状态。如果不引入额外的状态变量到肌腱动力学中，我们就无法做到这一点，因此需要一个额外的一阶常微分方程。对于这个状态，我们可以有很多选择，但或许最直观的是使用 \(\tilde{l}^M\)。有了这个，我们需要同时创建一个肌腱力（\(F^T\)）的表达式以及 \(\frac{d \tilde{l}^M}{dt}\) 的一阶常微分方程。\(l^M\)、\(l^T\) 和 \(\tilde{l}^T\) 的计算可以类似于刚性肌腱动力学，记住我们已经有了 \(\tilde{l}^M\) 作为一个已知值，因为它是一个状态变量。

\[\begin{split}l^M &= \tilde{l}^M \cdot l^M_{opt} \\ l^T &= l^{MT} - \sqrt{\left(l^M\right)^2 - \left(l^M_{opt} \sin{\alpha_{opt}}\right)^2} \\ \tilde{l}^T &= \frac{l^T}{l^T_{slack}}\end{split}\]

使用 \(\tilde{l}^T\) 和肌腱力-长度曲线 (\(fl^T\left(\tilde{l}^T\right)\))，我们可以写出归一化和绝对肌腱力的方程：

\[\begin{split}\tilde{F}^T &= fl^T\left(\tilde{l}^T\right) \\ F^T &= F^M_{max} \cdot \tilde{F}^T\end{split}\]

要表达 \(F^M\) ，我们需要知道羽状角 (\(\cos{\alpha}\)) 的余弦值。我们可以使用三角学来为此写一个方程：

\[\begin{split}\cos{\alpha} &= \frac{l^{MT} - l^T}{l^M} \\ F^M &= \frac{F^T}{\cos{\alpha}}\end{split}\]

如果我们假设阻尼系数 \(\beta = 0\)，我们可以重新排列肌肉纤维力方程：

\[\tilde{F}^M = a \cdot fl^M_{act}\left(\tilde{l}^M\right) \cdot fv^M\left(\tilde{v}^M\right) + fl^M_{pas}\left(\tilde{l}^M\right) + \beta \cdot \tilde{v}^M\]

给出 \(fv^M\left(\tilde{v}^M\right)\)：

\[fv^M\left(\tilde{v}^M\right) = \frac{\tilde{F}^M - fl^M_{pas}\left(\tilde{l}^M\right)}{a \cdot fl^M_{act}\left(\tilde{l}^M\right)}\]

使用逆纤维力-速度曲线，\(\left[fv^M\left(\tilde{v}^M\right)\right]^{-1}\)，并对 \(\tilde{l}^M\) 关于时间求导，我们可以最终写出 \(\frac{d \tilde{l}^M}{dt}\) 的方程：

\[\frac{d \tilde{l}^M}{dt} = \frac{v^M_{max}}{l^M_{opt}} \tilde{v}^M\]

To formulate these elastic tendon musculotendon dynamics, we had to assume that \(\beta = 0\), which is suboptimal in forward simulations and optimal control problems. It is possible to formulate elastic tendon musculotendon dynamics with damping, but this requires a more complicated formulation with an additional input variable in addition to an additional state variable, and as such the musculotendon dynamics must be enforced as a differential algebraic equation rather than an ordinary differential equation. The specifics of these types of formulation will not be discussed here, but the interested reader can refer to the docstrings of the MusculotendonDeGroote2016 where they are implemented.

一个简单的肌肉肌腱模型

为了演示肌肉对一个简单系统的影响，我们可以模拟一个质量为 \(m\) 的粒子，在肌肉对抗重力的作用下受到重力的影响。质量 \(m\) 有一个广义坐标 \(q\) 和广义速度 \(u\) 来描述其位置和运动。以下代码建立了运动学、重力以及相关的粒子：

>>> import pprint
>>> import sympy as sm
>>> import sympy.physics.mechanics as me

>>> q, u = me.dynamicsymbols('q, u', real=True)
>>> m, g = sm.symbols('m, g', real=True, positive=True)

>>> N = me.ReferenceFrame('N')
>>> O, P = sm.symbols('O, P', cls=me.Point)

>>> P.set_pos(O, q*N.x)
>>> O.set_vel(N, 0)
>>> P.set_vel(N, u*N.x)

>>> gravity = me.Force(P, m*g*N.x)

>>> block = me.Particle('block', P, m)

SymPy 生物力学包括肌腱驱动模型。这里我们将使用一个特定的肌腱模型实现。一个肌腱驱动器通过两个输入组件实例化，即路径和激活动力学模型。驱动器必须沿着连接肌肉起始点和插入点的路径作用。我们的起始点将连接到固定点 \(O\) ，并插入到移动粒子 \(P\) 上。

>>> from sympy.physics.mechanics.pathway import LinearPathway

>>> muscle_pathway = LinearPathway(O, P)

一条路径有附着点：

>>> muscle_pathway.attachments
(O, P)

并且知道末端附着点之间的距离以及两个附着点之间的相对速度：

>>> muscle_pathway.length
Abs(q(t))
>>> muscle_pathway.extension_velocity
sign(q(t))*Derivative(q(t), t)

最后，路径可以确定作用在两个附着点上的力，给出一个力的大小：

>>> muscle_pathway.to_loads(m*g)
[(O, - g*m*q(t)/Abs(q(t))*N.x), (P, g*m*q(t)/Abs(q(t))*N.x)]

激活动力学模型表示一组代数或常微分方程，这些方程将肌肉兴奋与肌肉激活联系起来。在我们的例子中，我们将使用一个一阶常微分方程，该方程从兴奋 \(e(t)\) 中给出平滑但延迟的激活 \(a(t)\)。

>>> from sympy.physics.biomechanics import FirstOrderActivationDeGroote2016
>>> muscle_activation = FirstOrderActivationDeGroote2016.with_defaults('muscle')

激活模型有一个状态变量 \(\mathbf{x}\)，输入变量 \(\mathbf{r}\)，以及一些常量参数 \(\mathbf{p}\)：

>>> muscle_activation.x
Matrix([[a_muscle(t)]])
>>> muscle_activation.r
Matrix([[e_muscle(t)]])
>>> muscle_activation.p
Matrix(0, 1, [])

Note that the return value for the constants parameters is empty. If we had instantiated FirstOrderActivationDeGroote2016 normally then we would have had to supply three values for \(\tau_{a}\), \(\tau_{d}\), and \(b\). If these had been Symbol objects then these would have shown up in the returned MutableDenseMatrix.

这些与其一阶微分方程 \(\dot{a} = f(a, e, t)\) 相关：

>>> muscle_activation.rhs()
Matrix([[((1/2 - tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2)/(0.0225*a_muscle(t) + 0.0075) + 16.6666666666667*(3*a_muscle(t)/2 + 1/2)*(tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2 + 1/2))*(-a_muscle(t) + e_muscle(t))]])

通过路径和激活动力学，使用这两者创建的肌腱模型需要一些参数来定义肌肉和肌腱的特定属性。你需要指定肌腱松弛长度、峰值等长力、最佳纤维长度、最大纤维速度、最佳羽状角和纤维阻尼系数。

>>> from sympy.physics.biomechanics import MusculotendonDeGroote2016

>>> F_M_max, l_M_opt, l_T_slack = sm.symbols('F_M_max, l_M_opt, l_T_slack', real=True)
>>> v_M_max, alpha_opt, beta = sm.symbols('v_M_max, alpha_opt, beta', real=True)

>>> muscle = MusculotendonDeGroote2016.with_defaults(
...     'muscle',
...     muscle_pathway,
...     muscle_activation,
...     tendon_slack_length=l_T_slack,
...     peak_isometric_force=F_M_max,
...     optimal_fiber_length=l_M_opt,
...     maximal_fiber_velocity=v_M_max,
...     optimal_pennation_angle=alpha_opt,
...     fiber_damping_coefficient=beta,
... )
...

因为这个肌肉肌腱执行器有一个刚性肌腱模型，它具有与激活模型相同的状态和常微分方程：

>>> muscle.musculotendon_dynamics
0
>>> muscle.x
Matrix([[a_muscle(t)]])
>>> muscle.r
Matrix([[e_muscle(t)]])
>>> muscle.p
Matrix([
[l_T_slack],
[  F_M_max],
[  l_M_opt],
[  v_M_max],
[alpha_opt],
[     beta]])
>>> muscle.rhs()
Matrix([[((1/2 - tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2)/(0.0225*a_muscle(t) + 0.0075) + 16.6666666666667*(3*a_muscle(t)/2 + 1/2)*(tanh(10.0*a_muscle(t) - 10.0*e_muscle(t))/2 + 1/2))*(-a_muscle(t) + e_muscle(t))]])

肌腱提供了额外的微分方程，以及施加在路径上的肌肉特异性力：

>>> muscle_loads = muscle.to_loads()
>>> pprint.pprint(muscle_loads)
[Force(point=O, force=F_M_max*(beta*(-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)) + a_muscle(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.6, 4.0))*q(t)*cos(alpha_opt)/Abs(q(t))*N.x),
 Force(point=P, force=- F_M_max*(beta*(-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)) + a_muscle(t)*FiberForceLengthActiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.814, 1.06, 0.162, 0.0633, 0.433, 0.717, -0.0299, 0.2, 0.1, 1.0, 0.354, 0.0)*FiberForceVelocityDeGroote2016((-l_T_slack + Abs(q(t)))*sign(q(t))*Derivative(q(t), t)/(v_M_max*sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)), -0.318, -8.149, -0.374, 0.886) + FiberForceLengthPassiveDeGroote2016(sqrt(l_M_opt**2*sin(alpha_opt)**2 + (-l_T_slack + Abs(q(t)))**2)/l_M_opt, 0.6, 4.0))*q(t)*cos(alpha_opt)/Abs(q(t))*N.x)]

这些负载由各种函数组成，这些函数描述了长度和速度与肌肉纤维力之间的关系。

既然我们已经有了肌肉和肌腱产生的力，就可以用例如Kane方法来形成系统的运动方程：

>>> kane = me.KanesMethod(N, (q,), (u,), kd_eqs=(u - q.diff(),))
>>> Fr, Frs = kane.kanes_equations((block,), (muscle_loads + [gravity]))

运动方程由运动学微分方程、动力学微分方程（牛顿第二定律）和肌肉激活微分方程组成。每个方程的显式形式可以如下形成：

>>> dqdt = u
>>> dudt = kane.forcing[0]/m
>>> dadt = muscle.rhs()[0]

我们现在可以创建一个数值函数，该函数根据给定的状态、输入和常量参数来评估运动方程。首先列出每个符号：

>>> a = muscle.a
>>> e = muscle.e
>>> state = [q, u, a]
>>> inputs = [e]
>>> constants = [m, g, F_M_max, l_M_opt, l_T_slack, v_M_max, alpha_opt, beta]

然后，用于评估显式常微分方程右侧的数值函数是：

>>> eval_eom = sm.lambdify((state, inputs, constants), (dqdt, dudt, dadt))

此外，数值评估肌肉力量也将是有趣的，因此也为它创建一个函数：

>>> force = muscle.force.xreplace({q.diff(): u})
>>> eval_force = sm.lambdify((state, constants), force)

为了测试这些功能，我们需要一些合适的数值。这块肌肉能够产生最大10 N的力来举起0.5 kg的质量：

>>> import numpy as np
>>> p_vals = np.array([
...     0.5,  # m [kg]
...     9.81,  # g [m/s/s]
...     10.0,  # F_M_max [N]
...     0.18,  # l_M_opt [m]
...     0.17,  # l_T_slack [m]
...     10.0,  # v_M_max [m/s]
...     0.0,  # alpha_opt
...     0.1,  # beta
... ])
...

我们的肌腱是刚性的，因此肌肉的长度将是 \(q-l_{T_ extrm{slack}}\) ，我们希望在产生力的峰值附近给予肌肉一个初始长度，因此我们选择 \(q_0=l_{M_ extrm{opt}} + l_{T_ extrm{slack}}\) 。让我们也给肌肉一个小的初始激活，以便它产生非零的力：

>>> x_vals = np.array([
...     p_vals[3] + p_vals[4],  # q [m]
...     0.0,  # u [m/s]
...     0.1,  # a [unitless]
... ])
...

将激励设置为1.0并测试数值函数：

>>> r_vals = np.array([
...     1.0,  # e
... ])
...
>>> eval_eom(x_vals, r_vals, p_vals)
(0.0, 7.817106179880225, 92.30769105034035)
>>> eval_force(x_vals, p_vals)
-0.9964469100598874

这两个函数可以工作，因此我们现在可以模拟这个系统，看看肌肉是否以及如何举起这个质量：

>>> def eval_rhs(t, x):
...
...     r = np.array([1.0])
...
...     return eval_eom(x, r, p_vals)
...
>>> from scipy.integrate import solve_ivp
>>> t0, tf = 0.0, 6.0
>>> times = np.linspace(t0, tf, num=601)
>>> sol = solve_ivp(eval_rhs,
...                 (t0, tf),
...                 x_vals, t_eval=times)
...
>>> import matplotlib.pyplot as plt
>>> fig, axes = plt.subplots(4, 1, sharex=True)
>>> _ = axes[0].plot(sol.t, sol.y[0] - p_vals[4], label='length of muscle')
>>> _ = axes[0].set_ylabel('Distance [m]')
>>> _ = axes[1].plot(sol.t, sol.y[1], label=state[1])
>>> _ = axes[1].set_ylabel('Speed [m/s]')
>>> _ = axes[2].plot(sol.t, sol.y[2], label=state[2])
>>> _ = axes[2].set_ylabel('Activation')
>>> _ = axes[3].plot(sol.t, eval_force(sol.y, p_vals).T, label='force')
>>> _ = axes[3].set_ylabel('Force [N]')
>>> _ = axes[3].set_xlabel('Time [s]')
>>> _ = axes[0].legend(), axes[1].legend(), axes[2].legend(), axes[3].legend()

(png, hires.png, pdf)

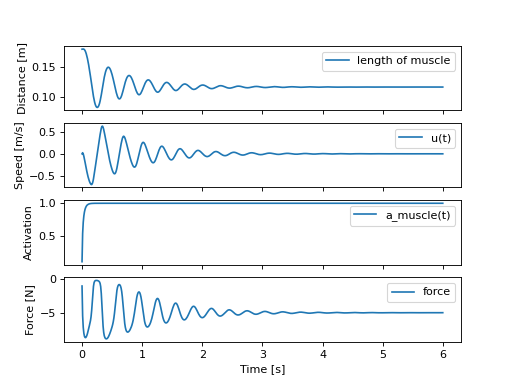
肌肉对抗重力拉动质量，并阻尼至5 N的平衡状态。

参考文献

[DeGroote2016] (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)

De Groote, F., Kinney, A. L., Rao, A. V., & Fregly, B. J., 直接配位最优控制问题公式化评估解决肌肉冗余问题, 生物医学工程年鉴, 44(10), (2016) pp. 2922-2936