多自由度全向系统¶
在这个例子中,我们演示了在 sympy.physics.mechanics 中提供的功能,用于推导包含粒子和刚体的完整系统的运动方程(EOM),这些系统包括作用力和力矩,其中一些是特定的力和力矩。系统如下所示:
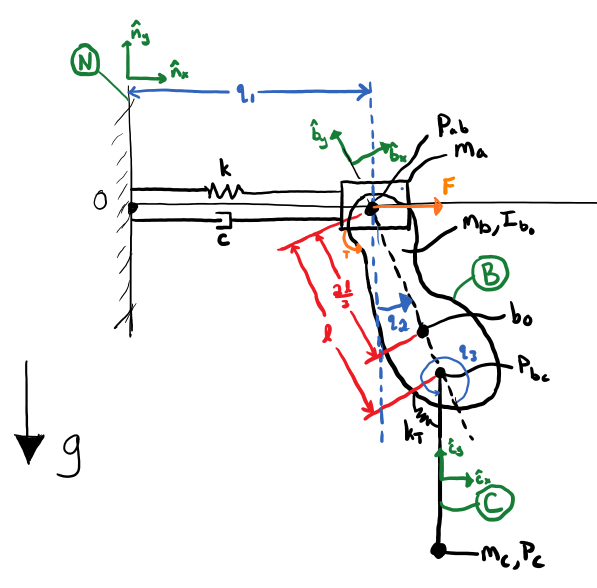
系统将使用 System 进行建模。首先,我们需要创建描述系统所需的 dynamicsymbols(),如上图所示。在这种情况下,广义坐标 \(q_1\) 表示块与墙之间的横向距离,\(q_2\) 表示复合摆从垂直方向的角度,\(q_3\) 表示简单摆从复合摆的角度。广义速度 \(u_1\) 表示块的横向速度,\(u_2\) 表示复合摆的横向速度,\(u_3\) 表示C相对于B的角速度。
我们还创建了一些 symbols() 来表示摆的长度、质量和重力等。:
>>> from sympy import zeros, symbols
>>> from sympy.physics.mechanics import *
>>> q1, q2, q3, u1, u2, u3 = dynamicsymbols('q1, q2, q3, u1, u2, u3')
>>> F, T = dynamicsymbols('F, T')
>>> l, k, c, g, kT = symbols('l, k, c, g, kT')
>>> ma, mb, mc, IBzz= symbols('ma, mb, mc, IBzz')
定义了所有符号后,我们现在可以定义主体并初始化我们的 System 实例。:
>>> wall = RigidBody('N')
>>> block = Particle('A', mass=ma)
>>> compound_pend = RigidBody('B', mass=mb)
>>> compound_pend.central_inertia = inertia(compound_pend.frame, 0, 0, IBzz)
>>> simple_pend = Particle('C', mass=mc)
>>> system = System.from_newtonian(wall)
>>> system.add_bodies(block, compound_pend, simple_pend)
接下来,我们使用关节连接物体以建立运动学。请注意,我们为两个粒子指定了中间框架,因为粒子没有关联的框架。
>>> block_frame = ReferenceFrame('A')
>>> block.masscenter.set_vel(block_frame, 0)
>>> slider = PrismaticJoint('J1', wall, block, coordinates=q1, speeds=u1,
... child_interframe=block_frame)
>>> rev1 = PinJoint('J2', block, compound_pend, coordinates=q2, speeds=u2,
... joint_axis=wall.z, child_point=l*2/3*compound_pend.y,
... parent_interframe=block_frame)
>>> simple_pend_frame = ReferenceFrame('C')
>>> simple_pend.masscenter.set_vel(simple_pend_frame, 0)
>>> rev2 = PinJoint('J3', compound_pend, simple_pend, coordinates=q3,
... speeds=u3, joint_axis=compound_pend.z,
... parent_point=-l/3*compound_pend.y,
... child_point=l*simple_pend_frame.y,
... child_interframe=simple_pend_frame)
>>> system.add_joints(slider, rev1, rev2)
现在我们可以对物体施加载荷(力和扭矩),重力作用于所有物体,线性弹簧和阻尼器作用于块和墙,旋转线性弹簧作用于C相对于B,指定的扭矩T作用于复合摆和块,指定的力F作用于块。:
>>> system.apply_uniform_gravity(-g * wall.y)
>>> system.add_loads(Force(block, F * wall.x))
>>> spring_damper_path = LinearPathway(wall.masscenter, block.masscenter)
>>> system.add_actuators(
... LinearSpring(k, spring_damper_path),
... LinearDamper(c, spring_damper_path),
... TorqueActuator(T, wall.z, compound_pend, wall),
... TorqueActuator(kT * q3, wall.z, compound_pend, simple_pend_frame),
... )
在系统设置完成后,我们现在可以使用后端的 KanesMethod 来形成运动方程。:
>>> system.form_eoms(explicit_kinematics=True)
Matrix([
[ -c*u1(t) - k*q1(t) + 2*l*mb*u2(t)**2*sin(q2(t))/3 - l*mc*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t)))*Derivative(u3(t), t) - l*mc*(-sin(q2(t))*cos(q3(t)) - sin(q3(t))*cos(q2(t)))*(u2(t) + u3(t))**2 + l*mc*u2(t)**2*sin(q2(t)) - (2*l*mb*cos(q2(t))/3 + mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))))*Derivative(u2(t), t) - (ma + mb + mc)*Derivative(u1(t), t) + F(t)],
[-2*g*l*mb*sin(q2(t))/3 - g*l*mc*(sin(q2(t))*cos(q3(t)) + sin(q3(t))*cos(q2(t))) - g*l*mc*sin(q2(t)) + l**2*mc*(u2(t) + u3(t))**2*sin(q3(t)) - l**2*mc*u2(t)**2*sin(q3(t)) - mc*(l**2*cos(q3(t)) + l**2)*Derivative(u3(t), t) - (2*l*mb*cos(q2(t))/3 + mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))))*Derivative(u1(t), t) - (IBzz + 4*l**2*mb/9 + mc*(2*l**2*cos(q3(t)) + 2*l**2))*Derivative(u2(t), t) + T(t)],
[ -g*l*mc*(sin(q2(t))*cos(q3(t)) + sin(q3(t))*cos(q2(t))) - kT*q3(t) - l**2*mc*u2(t)**2*sin(q3(t)) - l**2*mc*Derivative(u3(t), t) - l*mc*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t)))*Derivative(u1(t), t) - mc*(l**2*cos(q3(t)) + l**2)*Derivative(u2(t), t)]])
>>> system.mass_matrix_full
Matrix([
[1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, ma + mb + mc, 2*l*mb*cos(q2(t))/3 + mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))), l*mc*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t)))],
[0, 0, 0, 2*l*mb*cos(q2(t))/3 + mc*(l*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))) + l*cos(q2(t))), IBzz + 4*l**2*mb/9 + mc*(2*l**2*cos(q3(t)) + 2*l**2), mc*(l**2*cos(q3(t)) + l**2)],
[0, 0, 0, l*mc*(-sin(q2(t))*sin(q3(t)) + cos(q2(t))*cos(q3(t))), mc*(l**2*cos(q3(t)) + l**2), l**2*mc]])
>>> system.forcing_full
Matrix([
[ u1(t)],
[ u2(t)],
[ u3(t)],
[ -c*u1(t) - k*q1(t) + 2*l*mb*u2(t)**2*sin(q2(t))/3 - l*mc*(-sin(q2(t))*cos(q3(t)) - sin(q3(t))*cos(q2(t)))*(u2(t) + u3(t))**2 + l*mc*u2(t)**2*sin(q2(t)) + F(t)],
[-2*g*l*mb*sin(q2(t))/3 - g*l*mc*(sin(q2(t))*cos(q3(t)) + sin(q3(t))*cos(q2(t))) - g*l*mc*sin(q2(t)) + l**2*mc*(u2(t) + u3(t))**2*sin(q3(t)) - l**2*mc*u2(t)**2*sin(q3(t)) + T(t)],
[ -g*l*mc*(sin(q2(t))*cos(q3(t)) + sin(q3(t))*cos(q2(t))) - kT*q3(t) - l**2*mc*u2(t)**2*sin(q3(t))]])