矩阵 (线性代数)¶
创建矩阵¶
线性代数模块设计得尽可能简单。首先,我们导入并声明我们的第一个 Matrix 对象:
>>> from sympy.interactive.printing import init_printing
>>> init_printing(use_unicode=False)
>>> from sympy.matrices import Matrix, eye, zeros, ones, diag, GramSchmidt
>>> M = Matrix([[1,0,0], [0,0,0]]); M
[1 0 0]
[ ]
[0 0 0]
>>> Matrix([M, (0, 0, -1)])
[1 0 0 ]
[ ]
[0 0 0 ]
[ ]
[0 0 -1]
>>> Matrix([[1, 2, 3]])
[1 2 3]
>>> Matrix([1, 2, 3])
[1]
[ ]
[2]
[ ]
[3]
除了从适当大小的列表和/或矩阵列表创建矩阵外,SymPy 还支持更高级的矩阵创建方法,包括单个值列表和维度输入:
>>> Matrix(2, 3, [1, 2, 3, 4, 5, 6])
[1 2 3]
[ ]
[4 5 6]
更有趣(且有用)的是,可以使用一个双变量函数(或 lambda)来创建矩阵。这里我们创建了一个对角线上的指示函数,然后使用它来生成单位矩阵:
>>> def f(i,j):
... if i == j:
... return 1
... else:
... return 0
...
>>> Matrix(4, 4, f)
[1 0 0 0]
[ ]
[0 1 0 0]
[ ]
[0 0 1 0]
[ ]
[0 0 0 1]
最后,让我们使用 lambda 创建一个一行矩阵,其中偶排列项为1:
>>> Matrix(3, 4, lambda i,j: 1 - (i+j) % 2)
[1 0 1 0]
[ ]
[0 1 0 1]
[ ]
[1 0 1 0]
还有一些用于快速矩阵构造的特殊构造函数:eye 是单位矩阵,zeros 和 ones 分别用于全零和全一的矩阵,diag 用于将矩阵或元素沿对角线放置:
>>> eye(4)
[1 0 0 0]
[ ]
[0 1 0 0]
[ ]
[0 0 1 0]
[ ]
[0 0 0 1]
>>> zeros(2)
[0 0]
[ ]
[0 0]
>>> zeros(2, 5)
[0 0 0 0 0]
[ ]
[0 0 0 0 0]
>>> ones(3)
[1 1 1]
[ ]
[1 1 1]
[ ]
[1 1 1]
>>> ones(1, 3)
[1 1 1]
>>> diag(1, Matrix([[1, 2], [3, 4]]))
[1 0 0]
[ ]
[0 1 2]
[ ]
[0 3 4]
基本操作¶
在学习如何处理矩阵时,让我们选择一个条目易于识别的矩阵。需要知道的是,虽然矩阵是二维的,但存储不是,因此可以(尽管应该小心)像访问一维列表一样访问条目。
>>> M = Matrix(2, 3, [1, 2, 3, 4, 5, 6])
>>> M[4]
5
现在,更标准的条目访问是一对索引,它将始终返回矩阵中相应行和列的值:
>>> M[1, 2]
6
>>> M[0, 0]
1
>>> M[1, 1]
5
既然这是Python,我们也可以对子矩阵进行切片;切片总是返回一个矩阵,即使维度是1 x 1:
>>> M[0:2, 0:2]
[1 2]
[ ]
[4 5]
>>> M[2:2, 2]
[]
>>> M[:, 2]
[3]
[ ]
[6]
>>> M[:1, 2]
[3]
在上述的第二个例子中,注意切片 2:2 给出一个空范围。还要注意(与 Python 的基于 0 的索引一致)第一行/列是 0。
除非它们在一个切片中,否则您无法访问不存在的行或列:
>>> M[:, 10] # the 10-th column (not there)
Traceback (most recent call last):
...
IndexError: Index out of range: a[[0, 10]]
>>> M[:, 10:11] # the 10-th column (if there)
[]
>>> M[:, :10] # all columns up to the 10-th
[1 2 3]
[ ]
[4 5 6]
只要对没有大小的坐标使用切片,对空矩阵进行切片操作是有效的:
>>> Matrix(0, 3, [])[:, 1]
[]
切片会生成切片内容的副本,因此一个对象的修改不会影响另一个对象:
>>> M2 = M[:, :]
>>> M2[0, 0] = 100
>>> M[0, 0] == 100
False
注意,改变 M2 并没有改变 M。由于我们可以切片,我们也可以赋值条目:
>>> M = Matrix(([1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]))
>>> M
[1 2 3 4 ]
[ ]
[5 6 7 8 ]
[ ]
[9 10 11 12]
[ ]
[13 14 15 16]
>>> M[2,2] = M[0,3] = 0
>>> M
[1 2 3 0 ]
[ ]
[5 6 7 8 ]
[ ]
[9 10 0 12]
[ ]
[13 14 15 16]
以及分配切片:
>>> M = Matrix(([1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]))
>>> M[2:,2:] = Matrix(2,2,lambda i,j: 0)
>>> M
[1 2 3 4]
[ ]
[5 6 7 8]
[ ]
[9 10 0 0]
[ ]
[13 14 0 0]
所有标准算术运算都支持:
>>> M = Matrix(([1,2,3],[4,5,6],[7,8,9]))
>>> M - M
[0 0 0]
[ ]
[0 0 0]
[ ]
[0 0 0]
>>> M + M
[2 4 6 ]
[ ]
[8 10 12]
[ ]
[14 16 18]
>>> M * M
[30 36 42 ]
[ ]
[66 81 96 ]
[ ]
[102 126 150]
>>> M2 = Matrix(3,1,[1,5,0])
>>> M*M2
[11]
[ ]
[29]
[ ]
[47]
>>> M**2
[30 36 42 ]
[ ]
[66 81 96 ]
[ ]
[102 126 150]
以及一些有用的向量操作:
>>> M.row_del(0)
>>> M
[4 5 6]
[ ]
[7 8 9]
>>> M.col_del(1)
>>> M
[4 6]
[ ]
[7 9]
>>> v1 = Matrix([1,2,3])
>>> v2 = Matrix([4,5,6])
>>> v3 = v1.cross(v2)
>>> v1.dot(v2)
32
>>> v2.dot(v3)
0
>>> v1.dot(v3)
0
记住,row_del() 和 col_del() 操作不会返回值——它们只是改变矩阵对象。我们也可以将适当大小的矩阵 ‘’粘合’’ 在一起:
>>> M1 = eye(3)
>>> M2 = zeros(3, 4)
>>> M1.row_join(M2)
[1 0 0 0 0 0 0]
[ ]
[0 1 0 0 0 0 0]
[ ]
[0 0 1 0 0 0 0]
>>> M3 = zeros(4, 3)
>>> M1.col_join(M3)
[1 0 0]
[ ]
[0 1 0]
[ ]
[0 0 1]
[ ]
[0 0 0]
[ ]
[0 0 0]
[ ]
[0 0 0]
[ ]
[0 0 0]
条目操作¶
我们不仅限于在两个矩阵之间进行乘法:
>>> M = eye(3)
>>> 2*M
[2 0 0]
[ ]
[0 2 0]
[ ]
[0 0 2]
>>> 3*M
[3 0 0]
[ ]
[0 3 0]
[ ]
[0 0 3]
但我们也可以使用 applyfunc() 对矩阵条目应用函数。这里我们将声明一个将任何输入数字加倍的函数。然后我们将其应用于3x3单位矩阵:
>>> f = lambda x: 2*x
>>> eye(3).applyfunc(f)
[2 0 0]
[ ]
[0 2 0]
[ ]
[0 0 2]
如果你想从一个矩阵中提取一个公因子,你可以通过对矩阵的数据应用 gcd 来实现:
>>> from sympy.abc import x, y
>>> from sympy import gcd
>>> m = Matrix([[x, y], [1, x*y]]).inv('ADJ'); m
[ x*y -y ]
[-------- --------]
[ 2 2 ]
[x *y - y x *y - y]
[ ]
[ -1 x ]
[-------- --------]
[ 2 2 ]
[x *y - y x *y - y]
>>> gcd(tuple(_))
1
--------
2
x *y - y
>>> m/_
[x*y -y]
[ ]
[-1 x ]
另一个有用的矩阵范围的条目应用函数是替换函数。让我们声明一个带有符号条目的矩阵,然后替换一个值。记住我们可以替换任何东西——甚至是另一个符号!
>>> from sympy import Symbol
>>> x = Symbol('x')
>>> M = eye(3) * x
>>> M
[x 0 0]
[ ]
[0 x 0]
[ ]
[0 0 x]
>>> M.subs(x, 4)
[4 0 0]
[ ]
[0 4 0]
[ ]
[0 0 4]
>>> y = Symbol('y')
>>> M.subs(x, y)
[y 0 0]
[ ]
[0 y 0]
[ ]
[0 0 y]
线性代数¶
既然我们已经掌握了基础知识,让我们看看如何处理实际的矩阵。当然,首先想到的事情之一就是行列式:
>>> M = Matrix(( [1, 2, 3], [3, 6, 2], [2, 0, 1] ))
>>> M.det()
-28
>>> M2 = eye(3)
>>> M2.det()
1
>>> M3 = Matrix(( [1, 0, 0], [1, 0, 0], [1, 0, 0] ))
>>> M3.det()
0
另一个常见的操作是逆操作:在 SymPy 中,默认情况下通过高斯消元法计算(对于稠密矩阵),但我们也可以指定通过 \(LU\) 分解来完成:
>>> M2.inv()
[1 0 0]
[ ]
[0 1 0]
[ ]
[0 0 1]
>>> M2.inv(method="LU")
[1 0 0]
[ ]
[0 1 0]
[ ]
[0 0 1]
>>> M.inv(method="LU")
[-3/14 1/14 1/2 ]
[ ]
[-1/28 5/28 -1/4]
[ ]
[ 3/7 -1/7 0 ]
>>> M * M.inv(method="LU")
[1 0 0]
[ ]
[0 1 0]
[ ]
[0 0 1]
我们可以执行 \(QR\) 分解,这对于解决系统问题非常方便:
>>> A = Matrix([[1,1,1],[1,1,3],[2,3,4]])
>>> Q, R = A.QRdecomposition()
>>> Q
[ ___ ___ ___ ]
[\/ 6 -\/ 3 -\/ 2 ]
[----- ------- -------]
[ 6 3 2 ]
[ ]
[ ___ ___ ___ ]
[\/ 6 -\/ 3 \/ 2 ]
[----- ------- ----- ]
[ 6 3 2 ]
[ ]
[ ___ ___ ]
[\/ 6 \/ 3 ]
[----- ----- 0 ]
[ 3 3 ]
>>> R
[ ___ ]
[ ___ 4*\/ 6 ___]
[\/ 6 ------- 2*\/ 6 ]
[ 3 ]
[ ]
[ ___ ]
[ \/ 3 ]
[ 0 ----- 0 ]
[ 3 ]
[ ]
[ ___ ]
[ 0 0 \/ 2 ]
>>> Q*R
[1 1 1]
[ ]
[1 1 3]
[ ]
[2 3 4]
除了 solver.py 文件中的求解器之外,我们还可以通过将 b 向量传递给矩阵 A 的 LUsolve 函数来求解系统 Ax=b。这里我们稍微作弊一下,选择 A 和 x,然后相乘得到 b。然后我们可以求解 x 并检查其是否正确:
>>> A = Matrix([ [2, 3, 5], [3, 6, 2], [8, 3, 6] ])
>>> x = Matrix(3,1,[3,7,5])
>>> b = A*x
>>> soln = A.LUsolve(b)
>>> soln
[3]
[ ]
[7]
[ ]
[5]
还有一个不错的 Gram-Schmidt 正交化工具,它可以接受一组向量并相对于另一个向量进行正交化。有一个可选参数,用于指定输出是否也应该归一化,默认值为 False。让我们取一些向量并正交化它们——一个是归一化的,另一个不是:
>>> L = [Matrix([2,3,5]), Matrix([3,6,2]), Matrix([8,3,6])]
>>> out1 = GramSchmidt(L)
>>> out2 = GramSchmidt(L, True)
让我们来看看这些向量:
>>> for i in out1:
... print(i)
...
Matrix([[2], [3], [5]])
Matrix([[23/19], [63/19], [-47/19]])
Matrix([[1692/353], [-1551/706], [-423/706]])
>>> for i in out2:
... print(i)
...
Matrix([[sqrt(38)/19], [3*sqrt(38)/38], [5*sqrt(38)/38]])
Matrix([[23*sqrt(6707)/6707], [63*sqrt(6707)/6707], [-47*sqrt(6707)/6707]])
Matrix([[12*sqrt(706)/353], [-11*sqrt(706)/706], [-3*sqrt(706)/706]])
我们可以通过 dot() 检查它们的正交性,通过 norm() 检查它们的规范性:
>>> out1[0].dot(out1[1])
0
>>> out1[0].dot(out1[2])
0
>>> out1[1].dot(out1[2])
0
>>> out2[0].norm()
1
>>> out2[1].norm()
1
>>> out2[2].norm()
1
因此,该模块可以完成很多工作,包括特征值、特征向量、零空间计算、余子式展开工具等。从这里,您可能希望查看 matrices.py 文件以了解所有功能。
参考¶
矩阵基类¶
矩阵类是从各种基类中的功能构建的。Matrix 的每个方法和属性都在这些基类之一中实现。另请参阅 稠密矩阵 和 稀疏矩阵。
- class sympy.matrices.matrixbase.MatrixBase[源代码][源代码]¶
所有常见的矩阵操作,包括基本的算术运算、形状操作,以及特殊矩阵如 \(zeros\) 和 \(eye\)。
- 属性:
C逐元素共轭
D返回Dirac共轭(如果
self.rows == 4)。H返回厄米共轭。
T矩阵转置
- cols
free_symbols返回矩阵中的自由符号。
- is_Identity
is_echelon如果矩阵是阶梯形式,则返回 \(True\)。
is_hermitian检查矩阵是否为厄米矩阵。
is_indefinite找出矩阵的确定性。
is_lower检查矩阵是否为下三角矩阵。
is_lower_hessenberg检查矩阵是否为下Hessenberg形式。
is_negative_definite找出矩阵的确定性。
is_negative_semidefinite找出矩阵的确定性。
is_positive_definite找出矩阵的确定性。
is_positive_semidefinite找出矩阵的确定性。
is_square检查矩阵是否为方阵。
is_strongly_diagonally_dominant测试矩阵是否为行强对角占优。
is_upper检查矩阵是否为上三角矩阵。
is_upper_hessenberg检查矩阵是否为上Hessenberg形式。
is_weakly_diagonally_dominant测试矩阵是否为行弱对角占优。
is_zero_matrix检查一个矩阵是否为零矩阵。
- 种类
- 行
shape矩阵的形状(维度)作为 2 元组 (行数, 列数)。
方法
LDLdecomposition([hermitian])返回矩阵 A 的 LDL 分解 (L, D),使得如果 hermitian 标志为 True,则 L * D * L.H == A,或者如果 hermitian 为 False,则 L * D * L.T == A。
LDLsolve(rhs)使用LDL分解求解
Ax = B,适用于一般的方阵和非奇异矩阵。LUdecomposition([iszerofunc, simpfunc, ...])返回 (L, U, perm),其中 L 是一个对角线为单位矩阵的下三角矩阵,U 是一个上三角矩阵,perm 是一个行交换索引对的列表。
计算一个无分数的LU分解。
LUdecomposition_Simple([iszerofunc, ...])计算矩阵的 PLU 分解。
LUsolve(rhs[, iszerofunc])求解线性系统
Ax = rhs中的x,其中A = M。返回一个QR分解。
QRsolve(b)求解线性系统
Ax = b。add(b)返回 self + b。
adjoint()共轭转置或厄米共轭。
adjugate([method])返回矩阵的伴随矩阵,或经典伴随矩阵。
analytic_func(f, x)计算 f(A),其中 A 是一个方阵,f 是一个解析函数。
applyfunc(f)对矩阵的每个元素应用一个函数。
as_real_imag([deep])返回一个包含矩阵的(实部,虚部)部分的元组。
atoms(*types)返回构成当前对象的原子。
使用Berkowitz方法计算行列式。
berkowitz_eigenvals(**flags)使用Berkowitz方法计算矩阵的特征值。
使用Berkowitz方法计算主子式。
bidiagonal_decomposition([upper])返回 $(U,B,V.H)$ 用于
bidiagonalize([upper])返回 $B$,即输入矩阵的双对角化形式。
charpoly([x, simplify])计算特征多项式 det(x*I - M),其中 I 是单位矩阵。
cholesky([hermitian])返回矩阵 A 的 Cholesky 类型分解 L,使得如果 hermitian 标志为 True,则 L * L.H == A,或者如果 hermitian 为 False,则 L * L.T == A。
cholesky_solve(rhs)使用 Cholesky 分解求解
Ax = B,适用于一般的非奇异方阵。cofactor(i, j[, method])计算元素的余子式。
cofactor_matrix([method])返回一个包含每个元素的余子式的矩阵。
col(j)基本列选择器。
col_del(col)删除指定的列。
col_insert(pos, other)在给定的列位置插入一列或多列。
col_join(other)将两个矩阵沿着自身的最后一行和另一个矩阵的第一行进行连接。
columnspace([simplify])返回一个向量列表(矩阵对象),这些向量跨越
M的列空间companion(poly)返回多项式的伴随矩阵。
返回矩阵的条件数。
返回按元素的共轭。
当一个方阵被视为加权图时,返回图中连接顶点的列表。
仅使用排列将一个方阵分解为块对角形式。
copy()返回矩阵的副本。
cramer_solve(rhs[, det_method])使用克莱姆法则求解线性方程组。
cross(b)返回
self和b的叉积,放松兼容维度的条件:如果每个都有3个元素,将返回与self相同类型和形状的矩阵。det([method, iszerofunc])如果
M是一个具体的矩阵对象,则计算其行列式;否则,如果M是一个MatrixSymbol或其他表达式,则返回表达式Determinant(M)。使用LU分解计算矩阵行列式。
diag(*args[, strict, unpack, rows, cols])返回具有指定对角线的矩阵。
diagonal([k])返回自身的第 k 个对角线。
diagonal_solve(rhs)高效求解
Ax = B,其中 A 是一个对角矩阵,且对角元素非零。diagonalize([reals_only, sort, normalize])返回 (P, D),其中 D 是对角矩阵。
diff(*args[, evaluate])计算矩阵中每个元素的导数。
dot(b[, hermitian, conjugate_convention])返回两个长度相等的向量的点积或内积。
dual()返回矩阵的对偶。
echelon_form([iszerofunc, simplify, with_pivots])返回一个与
M行等价的矩阵,该矩阵为阶梯形式。eigenvals([error_when_incomplete])计算矩阵的特征值。
eigenvects([error_when_incomplete, iszerofunc])计算矩阵的特征向量。
elementary_col_op([op, col, k, col1, col2])执行基本列操作 \(op\)。
elementary_row_op([op, row, k, row1, row2])执行基本行操作 \(op\)。
evalf([n, subs, maxn, chop, strict, quad, ...])对 self 的每个元素应用 evalf()。
exp()返回一个方阵的指数。
expand([deep, modulus, power_base, ...])对矩阵的每个条目应用 core.function.expand。
extract(rowsList, colsList)通过指定行和列的列表返回一个子矩阵。
eye(rows[, cols])返回一个单位矩阵。
flat()返回矩阵中所有元素的扁平列表。
from_dok(rows, cols, dok)从键的字典创建一个矩阵。
gauss_jordan_solve(B[, freevar])使用高斯-约旦消元法求解
Ax = B。获取方阵主对角线上的子方阵。
has(*patterns)测试是否有任何子表达式匹配任何模式。
hat()返回表示叉积的反对称矩阵,使得
self.hat() * b等价于self.cross(b)。hstack(*args)返回一个矩阵,该矩阵通过水平连接参数(即通过重复应用 row_join)形成。
integrate(*args, **kwargs)积分矩阵的每个元素。
inv([method, iszerofunc, try_block_diag])使用指定方法返回矩阵的逆。
inverse_ADJ([iszerofunc])使用伴随矩阵和行列式计算逆矩阵。
inverse_BLOCK([iszerofunc])使用块状逆运算计算逆矩阵。
inverse_CH([iszerofunc])使用 Cholesky 分解计算逆矩阵。
inverse_GE([iszerofunc])使用高斯消去法计算逆矩阵。
inverse_LDL([iszerofunc])使用 LDL 分解计算逆矩阵。
inverse_LU([iszerofunc])使用LU分解计算逆矩阵。
inverse_QR([iszerofunc])使用QR分解计算逆矩阵。
irregular(ntop, *matrices, **kwargs)返回一个矩阵,该矩阵由给定的矩阵填充,这些矩阵按从左到右、从上到下的顺序依次出现,与它们在矩阵中首次出现的位置一致。
is_anti_symmetric([simplify])检查矩阵 M 是否为反对称矩阵,即,M 是一个方阵,且所有 M[i, j] == -M[j, i]。
检查矩阵是否为对角矩阵,即主对角线以外的所有元素均为零的矩阵。
is_diagonalizable([reals_only])如果矩阵可对角化,则返回
True。检查矩阵是否为幂零矩阵。
检查是否有元素包含符号。
is_symmetric([simplify])检查矩阵是否为对称矩阵,即方阵且等于其转置矩阵。
遍历非零项的索引和值。
遍历 self 的非零值
jacobian(X)计算雅可比矩阵(向量值函数的导数)。
jordan_block([size, eigenvalue, band])返回一个 Jordan 块
jordan_form([calc_transform])返回 $(P, J)$,其中 $J$ 是一个约旦块矩阵,$P$ 是一个矩阵,使得 $M = P J P^{-1}$
key2bounds(keys)将一个可能包含混合类型键(整数和切片)的键转换为范围元组,如果任何索引超出
self的范围,则引发错误。key2ij(key)将键转换为规范形式,将整数或可索引项转换为
self范围内的有效整数,或者返回切片不变。left_eigenvects(**flags)返回左特征向量和特征值。
limit(*args)计算矩阵中每个元素的极限。
log([simplify])返回一个方阵的对数。
lower_triangular([k])返回矩阵中第k条对角线及其以下的元素。
求解
Ax = B,其中 A 是一个下三角矩阵。minor(i, j[, method])返回
M的 (i,j) 子式。minor_submatrix(i, j)返回通过从
M中移除第 \(i\) 行和第 \(j\) 列得到的子矩阵(适用于Python风格的负索引)。multiply(other[, dotprodsimp])与 __mul__() 相同,但带有可选的简化。
multiply_elementwise(other)返回 A 和 B 的哈达玛积(逐元素乘积)
n(*args, **kwargs)对 self 的每个元素应用 evalf()。
norm([ord])返回矩阵或向量的范数。
normalized([iszerofunc])返回
self的规范化版本。nullspace([simplify, iszerofunc])返回一个向量列表(矩阵对象),这些向量跨越
M的零空间ones(rows[, cols])返回一个全为1的矩阵。
orthogonalize(*vecs, **kwargs)对
vecs中的向量应用格拉姆-施密特正交化过程。per()返回矩阵的永久值。
permute(perm[, orientation, direction])通过给定的交换列表置换矩阵的行或列。
permuteBkwd(perm)使用给定的排列逆序置换矩阵的行。
permuteFwd(perm)使用给定的排列来置换矩阵的行。
permute_cols(swaps[, direction])self.permute(swaps, orientation='cols', direction=direction)的别名permute_rows(swaps[, direction])self.permute(swaps, orientation='rows', direction=direction)的别名pinv([method])计算矩阵的 Moore-Penrose 伪逆。
pinv_solve(B[, arbitrary_matrix])使用 Moore-Penrose 伪逆求解
Ax = B。pow(exp[, method])返回 self**exp,其中 exp 是一个标量或符号。
print_nonzero([symb])显示非零条目的位置,以便快速查找形状。
project(v)返回
self在包含v的直线上的投影。rank([iszerofunc, simplify])返回矩阵的秩。
rank_decomposition([iszerofunc, simplify])返回一对矩阵 (\(C\), \(F\)),它们的秩相匹配,使得 \(A = C F\)。
refine([assumptions])对矩阵的每个元素应用细化。
replace(F, G[, map, simultaneous, exact])将矩阵条目中的函数 F 替换为函数 G。
reshape(rows, cols)重塑矩阵。
rmultiply(other[, dotprodsimp])与 __rmul__() 相同,但带有可选的简化功能。
rot90([k])将矩阵旋转90度
row(i)基本行选择器。
row_del(row)删除指定的行。
row_insert(pos, other)在给定的行位置插入一行或多行。
row_join(other)将两个矩阵沿着自身的最后一列和rhs的第一列进行连接
rowspace([simplify])返回一个向量列表,这些向量跨越矩阵
M的行空间。rref([iszerofunc, simplify, pivots, ...])返回矩阵的简化行阶梯形式和主元变量的索引。
rref_rhs(rhs)返回矩阵的简化行阶梯形式,显示简化步骤后的右侧矩阵。
simplify(**kwargs)对矩阵的每个元素应用简化。
返回一个压缩的奇异值分解。
计算矩阵的奇异值
solve(rhs[, method])求解存在唯一解的线性方程。
solve_least_squares(rhs[, method])返回对数据的最小二乘拟合。
当一个方阵被视为加权图时,返回图中强连通顶点的列表。
仅使用排列将一个方阵分解为块三角形式。
subs(*args, **kwargs)返回一个新的矩阵,其中每个条目都应用了 subs。
table(printer[, rowstart, rowend, rowsep, ...])以表格形式表示的矩阵字符串。
todod()返回矩阵作为包含矩阵非零元素的字典的字典
todok()返回矩阵作为键的字典。
tolist()返回矩阵作为嵌套的Python列表。
trace()返回一个方阵的迹,即对角元素之和。
返回矩阵的转置。
将一个矩阵转换为Hessenberg矩阵H。
upper_triangular([k])返回矩阵中第 k 条对角线及其以上的元素。
求解
Ax = B,其中 A 是一个上三角矩阵。values()返回 self 的非零值。
vec()通过堆叠列将矩阵转换为一列矩阵
vech([diagonal, check_symmetry])通过堆叠下三角中的元素,将矩阵重塑为列向量。
vee()从表示叉积的反对称矩阵返回一个3x1向量,使得
self * b等价于self.vee().cross(b)。vstack(*args)返回一个矩阵,该矩阵是通过垂直连接参数(即通过重复应用 col_join)形成的。
wilkinson(n, **kwargs)返回两个大小为 2*n + 1 的平方 Wilkinson 矩阵 $W_{2n + 1}^-, W_{2n + 1}^+ =$ Wilkinson(n)
xreplace(rule)返回一个新的矩阵,其中每个条目都应用了 xreplace。
zeros(rows[, cols])返回一个零矩阵。
berkowitz
berkowitz_charpoly
cofactorMatrix
det_bareis
执行
jordan_cell
jordan_cells
minorEntry
minorMatrix
- property C¶
逐元素共轭
- property D¶
返回Dirac共轭(如果
self.rows == 4)。参见
示例
>>> from sympy import Matrix, I, eye >>> m = Matrix((0, 1 + I, 2, 3)) >>> m.D Matrix([[0, 1 - I, -2, -3]]) >>> m = (eye(4) + I*eye(4)) >>> m[0, 3] = 2 >>> m.D Matrix([ [1 - I, 0, 0, 0], [ 0, 1 - I, 0, 0], [ 0, 0, -1 + I, 0], [ 2, 0, 0, -1 + I]])
如果矩阵没有4行,将会引发一个 AttributeError,因为此属性仅针对具有4行的矩阵定义。
>>> Matrix(eye(2)).D Traceback (most recent call last): ... AttributeError: Matrix has no attribute D.
- property H¶
返回厄米共轭。
参见
conjugate逐元素共轭
sympy.matrices.matrixbase.MatrixBase.DDirac 共轭
示例
>>> from sympy import Matrix, I >>> m = Matrix((0, 1 + I, 2, 3)) >>> m Matrix([ [ 0], [1 + I], [ 2], [ 3]]) >>> m.H Matrix([[0, 1 - I, 2, 3]])
- LDLdecomposition(hermitian=True)[源代码][源代码]¶
返回矩阵 A 的 LDL 分解 (L, D),使得如果 hermitian 标志为 True,则 L * D * L.H == A,如果 hermitian 为 False,则 L * D * L.T == A。此方法消除了平方根的使用。此外,这确保了 L 的所有对角线项均为 1。如果 hermitian 为 True,则 A 必须是 Hermitian 正定矩阵,否则 A 必须是对称矩阵。
参见
示例
>>> from sympy import Matrix, eye >>> A = Matrix(((25, 15, -5), (15, 18, 0), (-5, 0, 11))) >>> L, D = A.LDLdecomposition() >>> L Matrix([ [ 1, 0, 0], [ 3/5, 1, 0], [-1/5, 1/3, 1]]) >>> D Matrix([ [25, 0, 0], [ 0, 9, 0], [ 0, 0, 9]]) >>> L * D * L.T * A.inv() == eye(A.rows) True
矩阵可以有复数项:
>>> from sympy import I >>> A = Matrix(((9, 3*I), (-3*I, 5))) >>> L, D = A.LDLdecomposition() >>> L Matrix([ [ 1, 0], [-I/3, 1]]) >>> D Matrix([ [9, 0], [0, 4]]) >>> L*D*L.H == A True
- LDLsolve(rhs)[源代码][源代码]¶
使用LDL分解求解
Ax = B,适用于一般的方阵和非奇异矩阵。对于行数大于列数的非方阵,返回最小二乘解。
参见
示例
>>> from sympy import Matrix, eye >>> A = eye(2)*2 >>> B = Matrix([[1, 2], [3, 4]]) >>> A.LDLsolve(B) == B/2 True
- LUdecomposition(
- iszerofunc=<function _iszero>,
- simpfunc=None,
- rankcheck=False,
返回 (L, U, perm),其中 L 是一个对角线为单位元的下三角矩阵,U 是一个上三角矩阵,perm 是一个行交换索引对的列表。如果 A 是原始矩阵,那么
A = (L*U).permuteBkwd(perm),并且行置换矩阵 P 使得 \(P A = L U\) 可以通过P = eye(A.rows).permuteFwd(perm)计算。有关关键字参数 rankcheck、iszerofunc 和 simpfunc 的详细信息,请参阅 LUCombined 的文档。
- 参数:
- rankcheckbool, 可选
确定此函数是否应检测矩阵的秩不足,并应引发
ValueError。- iszerofunc函数, 可选
一个判断给定表达式是否为零的函数。
该函数应为一个可调用对象,它接受一个 SymPy 表达式并返回一个三值布尔值
True、False或None。它在内部被枢轴搜索算法使用。有关枢轴搜索算法的更多信息,请参见注释部分。
- simpfunc函数或无,可选
一个简化输入的函数。
如果将其指定为一个函数,该函数应是一个可调用对象,它接受一个 SymPy 表达式并返回另一个代数等价的 SymPy 表达式。
如果
None,则表示枢轴搜索算法不应尝试简化任何候选枢轴。它在内部被枢轴搜索算法使用。有关枢轴搜索算法的更多信息,请参见注释部分。
参见
示例
>>> from sympy import Matrix >>> a = Matrix([[4, 3], [6, 3]]) >>> L, U, _ = a.LUdecomposition() >>> L Matrix([ [ 1, 0], [3/2, 1]]) >>> U Matrix([ [4, 3], [0, -3/2]])
- LUdecompositionFF()[源代码][源代码]¶
计算一个无分数的LU分解。
返回4个矩阵 P, L, D, U 使得 PA = L D**-1 U。如果矩阵的元素属于某个整数域 I,那么 L, D 和 U 的所有元素都保证属于 I。
参考文献
[1]W. Zhou & D.J. Jeffrey, “Fraction-free matrix factors: new forms for LU and QR factors”. Frontiers in Computer Science in China, Vol 2, no. 1, pp. 67-80, 2008.
- LUdecomposition_Simple(
- iszerofunc=<function _iszero>,
- simpfunc=None,
- rankcheck=False,
计算矩阵的 PLU 分解。
- 参数:
- rankcheckbool, 可选
确定此函数是否应检测矩阵的秩不足,并应引发
ValueError。- iszerofunc函数, 可选
一个判断给定表达式是否为零的函数。
该函数应为一个可调用对象,它接受一个 SymPy 表达式并返回一个三值布尔值
True、False或None。它在内部被枢轴搜索算法使用。有关枢轴搜索算法的更多信息,请参见注释部分。
- simpfunc函数或无,可选
一个简化输入的函数。
如果将其指定为一个函数,该函数应是一个可调用对象,它接受一个 SymPy 表达式并返回另一个代数等价的 SymPy 表达式。
如果
None,则表示枢轴搜索算法不应尝试简化任何候选枢轴。它在内部被枢轴搜索算法使用。有关枢轴搜索算法的更多信息,请参见注释部分。
- 返回:
- (lu, row_swaps)(矩阵, 列表)
如果原始矩阵是一个 \(m, n\) 矩阵:
lu 是一个 \(m, n\) 矩阵,它以压缩形式包含分解结果。请参阅注释部分以了解矩阵如何被压缩。
row_swaps 是一个 \(m\) 元素的列表,其中每个元素是一对行交换的索引。
A = (L*U).permute_backward(perm),以及公式 \(P A = L U\) 中的行置换矩阵 \(P\) 可以通过P=eye(A.row).permute_forward(perm)计算。
- Raises:
- ValueError
如果在计算过程中发现矩阵秩不足,并且
rankcheck=True,则会引发此异常。
注释
关于PLU分解:
PLU 分解是 LU 分解的推广,可以扩展用于秩亏矩阵。
它还可以推广到非方阵,这是SymPy使用的符号。
PLU 分解是对一个 \(m, n\) 矩阵 \(A\) 的分解,形式为 \(P A = L U\) 其中
- \(L\) 是一个 \(m, m\) 的下三角矩阵,且对角线元素为1。
entries.
\(U\) 是一个 \(m, n\) 上三角矩阵。
\(P\) 是一个 \(m, m\) 的置换矩阵。
因此,对于一个方阵,分解看起来像这样:
\[\begin{split}L = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ L_{1, 0} & 1 & 0 & \cdots & 0 \\ L_{2, 0} & L_{2, 1} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ L_{n-1, 0} & L_{n-1, 1} & L_{n-1, 2} & \cdots & 1 \end{bmatrix}\end{split}\]\[\begin{split}U = \begin{bmatrix} U_{0, 0} & U_{0, 1} & U_{0, 2} & \cdots & U_{0, n-1} \\ 0 & U_{1, 1} & U_{1, 2} & \cdots & U_{1, n-1} \\ 0 & 0 & U_{2, 2} & \cdots & U_{2, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & U_{n-1, n-1} \end{bmatrix}\end{split}\]而对于行数多于列数的矩阵,分解将如下所示:
\[\begin{split}L = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ L_{1, 0} & 1 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ L_{2, 0} & L_{2, 1} & 1 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ L_{n-1, 0} & L_{n-1, 1} & L_{n-1, 2} & \cdots & 1 & 0 & \cdots & 0 \\ L_{n, 0} & L_{n, 1} & L_{n, 2} & \cdots & L_{n, n-1} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ L_{m-1, 0} & L_{m-1, 1} & L_{m-1, 2} & \cdots & L_{m-1, n-1} & 0 & \cdots & 1 \\ \end{bmatrix}\end{split}\]\[\begin{split}U = \begin{bmatrix} U_{0, 0} & U_{0, 1} & U_{0, 2} & \cdots & U_{0, n-1} \\ 0 & U_{1, 1} & U_{1, 2} & \cdots & U_{1, n-1} \\ 0 & 0 & U_{2, 2} & \cdots & U_{2, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & U_{n-1, n-1} \\ 0 & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 0 \end{bmatrix}\end{split}\]最后,对于列数多于行数的矩阵,分解将如下所示:
\[\begin{split}L = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ L_{1, 0} & 1 & 0 & \cdots & 0 \\ L_{2, 0} & L_{2, 1} & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ L_{m-1, 0} & L_{m-1, 1} & L_{m-1, 2} & \cdots & 1 \end{bmatrix}\end{split}\]\[\begin{split}U = \begin{bmatrix} U_{0, 0} & U_{0, 1} & U_{0, 2} & \cdots & U_{0, m-1} & \cdots & U_{0, n-1} \\ 0 & U_{1, 1} & U_{1, 2} & \cdots & U_{1, m-1} & \cdots & U_{1, n-1} \\ 0 & 0 & U_{2, 2} & \cdots & U_{2, m-1} & \cdots & U_{2, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \cdots & \vdots \\ 0 & 0 & 0 & \cdots & U_{m-1, m-1} & \cdots & U_{m-1, n-1} \\ \end{bmatrix}\end{split}\]关于压缩的LU存储:
分解的结果通常以压缩形式存储,而不是分别返回 \(L\) 和 \(U\) 矩阵。
它可能不那么直观,但由于其效率,它通常被用于许多数值库。
对于这种方法,存储矩阵定义如下:
- 矩阵 \(L\) 的次对角线元素存储在次对角线上。
部分 \(LU\),即 \(LU_{i, j} = L_{i, j}\) 当 \(i > j\) 时。
- 矩阵 \(L\) 的对角线元素都是 1,并且这些元素不
显式存储。
- \(U\) 存储在 \(LU\) 的上三角部分,即
\(LU_{i, j} = U_{i, j}\) 当 \(i <= j\) 时。
- 对于 \(m > n\) 的情况,\(L\) 矩阵的右侧是
易于存储。
- 对于 \(m < n\) 的情况,\(U\) 矩阵的下方是
易于存储。
因此,对于一个方阵,压缩后的输出矩阵将是:
\[\begin{split}LU = \begin{bmatrix} U_{0, 0} & U_{0, 1} & U_{0, 2} & \cdots & U_{0, n-1} \\ L_{1, 0} & U_{1, 1} & U_{1, 2} & \cdots & U_{1, n-1} \\ L_{2, 0} & L_{2, 1} & U_{2, 2} & \cdots & U_{2, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ L_{n-1, 0} & L_{n-1, 1} & L_{n-1, 2} & \cdots & U_{n-1, n-1} \end{bmatrix}\end{split}\]对于行数多于列数的矩阵,压缩输出矩阵将是:
\[\begin{split}LU = \begin{bmatrix} U_{0, 0} & U_{0, 1} & U_{0, 2} & \cdots & U_{0, n-1} \\ L_{1, 0} & U_{1, 1} & U_{1, 2} & \cdots & U_{1, n-1} \\ L_{2, 0} & L_{2, 1} & U_{2, 2} & \cdots & U_{2, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ L_{n-1, 0} & L_{n-1, 1} & L_{n-1, 2} & \cdots & U_{n-1, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ L_{m-1, 0} & L_{m-1, 1} & L_{m-1, 2} & \cdots & L_{m-1, n-1} \\ \end{bmatrix}\end{split}\]对于列数多于行数的矩阵,压缩输出矩阵将是:
\[\begin{split}LU = \begin{bmatrix} U_{0, 0} & U_{0, 1} & U_{0, 2} & \cdots & U_{0, m-1} & \cdots & U_{0, n-1} \\ L_{1, 0} & U_{1, 1} & U_{1, 2} & \cdots & U_{1, m-1} & \cdots & U_{1, n-1} \\ L_{2, 0} & L_{2, 1} & U_{2, 2} & \cdots & U_{2, m-1} & \cdots & U_{2, n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \cdots & \vdots \\ L_{m-1, 0} & L_{m-1, 1} & L_{m-1, 2} & \cdots & U_{m-1, m-1} & \cdots & U_{m-1, n-1} \\ \end{bmatrix}\end{split}\]关于枢轴搜索算法:
当矩阵包含符号项时,主元搜索算法与所有项都可以归类为零或非零的情况不同。该算法逐列搜索子矩阵,该子矩阵的左上角项与主元位置重合。如果存在,主元是当前搜索列中 iszerofunc 保证为非零的第一个项。如果没有这样的候选者,那么如果 simpfunc 不是 None,则每个候选主元都会被简化。搜索会重复进行,不同的是,如果
iszerofunc()不能保证其为非零,则候选者可能成为主元。在第二次搜索中,主元是 iszerofunc 能保证为非零的第一个候选者。如果没有这样的候选者,那么主元是 iszerofunc 返回 None 的第一个候选者。如果没有这样的候选者,那么搜索会在右边下一列重复进行。主元搜索算法与rref()中的算法不同,后者依赖于_find_reasonable_pivot()。未来版本的LUdecomposition_simple()可能会使用_find_reasonable_pivot()。
- LUsolve(
- rhs,
- iszerofunc=<function _iszero>,
求解线性系统
Ax = rhs中的x,其中A = M。这是用于符号矩阵的,对于实数或复数矩阵,请使用 mpmath.lu_solve 或 mpmath.qr_solve。
- QRdecomposition()[源代码][源代码]¶
返回一个QR分解。
参见
示例
满秩矩阵示例:
>>> from sympy import Matrix >>> A = Matrix([[12, -51, 4], [6, 167, -68], [-4, 24, -41]]) >>> Q, R = A.QRdecomposition() >>> Q Matrix([ [ 6/7, -69/175, -58/175], [ 3/7, 158/175, 6/175], [-2/7, 6/35, -33/35]]) >>> R Matrix([ [14, 21, -14], [ 0, 175, -70], [ 0, 0, 35]])
如果矩阵是方阵且满秩,\(Q\) 矩阵在两个方向上都变为正交,不需要增广。
>>> Q * Q.H Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]]) >>> Q.H * Q Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]])
>>> A == Q*R True
秩不足矩阵示例:
>>> A = Matrix([[12, -51, 0], [6, 167, 0], [-4, 24, 0]]) >>> Q, R = A.QRdecomposition() >>> Q Matrix([ [ 6/7, -69/175], [ 3/7, 158/175], [-2/7, 6/35]]) >>> R Matrix([ [14, 21, 0], [ 0, 175, 0]])
QR分解可能会返回一个矩形的矩阵Q。在这种情况下,正交条件可能在\(\mathbb{I} = Q.H*Q\)中满足,但在逆乘积\(\mathbb{I} = Q * Q.H\)中不满足。
>>> Q.H * Q Matrix([ [1, 0], [0, 1]]) >>> Q * Q.H Matrix([ [27261/30625, 348/30625, -1914/6125], [ 348/30625, 30589/30625, 198/6125], [ -1914/6125, 198/6125, 136/1225]])
如果你想将结果扩展为完整的正交分解,你应该用另一个正交列来扩展 \(Q\)。
你可以附加一个单位矩阵,并且你可以运行 Gram-Schmidt 过程使它们增广为正交基。
>>> Q_aug = Q.row_join(Matrix.eye(3)) >>> Q_aug = Q_aug.QRdecomposition()[0] >>> Q_aug Matrix([ [ 6/7, -69/175, 58/175], [ 3/7, 158/175, -6/175], [-2/7, 6/35, 33/35]]) >>> Q_aug.H * Q_aug Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]]) >>> Q_aug * Q_aug.H Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]])
将零行添加到 \(R\) 矩阵中是直接的。
>>> R_aug = R.col_join(Matrix([[0, 0, 0]])) >>> R_aug Matrix([ [14, 21, 0], [ 0, 175, 0], [ 0, 0, 0]]) >>> Q_aug * R_aug == A True
零矩阵示例:
>>> from sympy import Matrix >>> A = Matrix.zeros(3, 4) >>> Q, R = A.QRdecomposition()
它们可能会返回具有零行和零列的矩阵。
>>> Q Matrix(3, 0, []) >>> R Matrix(0, 4, []) >>> Q*R Matrix([ [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])
与上述相同的增强规则,\(Q\) 可以用单位矩阵的列来增强,\(R\) 可以用零矩阵的行来增强。
>>> Q_aug = Q.row_join(Matrix.eye(3)) >>> R_aug = R.col_join(Matrix.zeros(3, 4)) >>> Q_aug * Q_aug.T Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]]) >>> R_aug Matrix([ [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]) >>> Q_aug * R_aug == A True
- QRsolve(b)[源代码][源代码]¶
求解线性系统
Ax = b。M是矩阵A,方法参数是向量b。该方法返回解向量x。如果b是一个矩阵,则系统为b的每一列求解,返回值是一个与b形状相同的矩阵。这种方法较慢(大约慢2倍),但对于浮点运算比LUsolve方法更稳定。然而,LUsolve通常使用精确运算,因此你不需要使用QRsolve。
这主要是为了教育和符号矩阵的目的,对于实数(或复数)矩阵,请使用 mpmath.qr_solve。
- property T¶
矩阵转置
- __getitem__(key)[源代码][源代码]¶
实现 __getitem__ 应接受整数,在这种情况下,矩阵被索引为平面列表,元组 (i,j) 在这种情况下返回 (i,j) 条目,切片,或混合元组 (a,b) 其中 a 和 b 是切片和整数的任何组合。
- __mul__(other)[源代码][源代码]¶
返回 self*other,其中 other 可以是标量或维度兼容的矩阵。
参见
matrix_multiply_elementwise
示例
>>> from sympy import Matrix >>> A = Matrix([[1, 2, 3], [4, 5, 6]]) >>> 2*A == A*2 == Matrix([[2, 4, 6], [8, 10, 12]]) True >>> B = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> A*B Matrix([ [30, 36, 42], [66, 81, 96]]) >>> B*A Traceback (most recent call last): ... ShapeError: Matrices size mismatch. >>>
- __weakref__¶
对象的弱引用列表(如果已定义)
- adjugate(method='berkowitz')[源代码][源代码]¶
返回矩阵的伴随矩阵,或经典伴随矩阵。即,余子式矩阵的转置。
https://en.wikipedia.org/wiki/Adjugate
- 参数:
- 方法字符串,可选
用于查找余子式的方法,可以是“bareiss”、“berkowitz”、“bird”、“laplace”或“lu”。
示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2], [3, 4]]) >>> M.adjugate() Matrix([ [ 4, -2], [-3, 1]])
- analytic_func(f, x)[源代码][源代码]¶
计算 f(A),其中 A 是一个方阵,f 是一个解析函数。
- 参数:
- f表达式
分析函数
- x符号
f 的参数
示例
>>> from sympy import Symbol, Matrix, S, log
>>> x = Symbol('x') >>> m = Matrix([[S(5)/4, S(3)/4], [S(3)/4, S(5)/4]]) >>> f = log(x) >>> m.analytic_func(f, x) Matrix([ [ 0, log(2)], [log(2), 0]])
- applyfunc(f)[源代码][源代码]¶
对矩阵的每个元素应用一个函数。
示例
>>> from sympy import Matrix >>> m = Matrix(2, 2, lambda i, j: i*2+j) >>> m Matrix([ [0, 1], [2, 3]]) >>> m.applyfunc(lambda i: 2*i) Matrix([ [0, 2], [4, 6]])
- atoms(*types)[源代码][源代码]¶
返回构成当前对象的原子。
示例
>>> from sympy.abc import x, y >>> from sympy import Matrix >>> Matrix([[x]]) Matrix([[x]]) >>> _.atoms() {x} >>> Matrix([[x, y], [y, x]]) Matrix([ [x, y], [y, x]]) >>> _.atoms() {x, y}
- bidiagonal_decomposition(upper=True)[源代码][源代码]¶
返回 \((U,B,V.H)\) 用于
\[A = UBV^{H}\]其中 \(A\) 是输入矩阵,而 \(B\) 是其双对角化形式
注意:双对角计算对于符号矩阵可能会卡住。
- 参数:
- 上部bool. 是否进行上双对角化或下双对角化。
True 表示大写,False 表示小写。
参考文献
[1]算法 5.4.2,由 Golub 和 Van Loan 编写的矩阵计算,第 4 版
- bidiagonalize(upper=True)[源代码][源代码]¶
返回 \(B\),即输入矩阵的双对角化形式。
注意:双对角计算对于符号矩阵可能会卡住。
- 参数:
- 上部bool. 是否进行上双对角化或下双对角化。
True 表示大写,False 表示小写。
参考文献
[1]算法 5.4.2,由 Golub 和 Van Loan 编写的矩阵计算,第 4 版
[2]复杂矩阵双对角化 : https://github.com/vslobody/Householder-Bidiagonalization
- charpoly(
- x='lambda',
- simplify=<function _simplify>,
计算特征多项式 det(x*I - M),其中 I 是单位矩阵。
返回的是一个 PurePoly,因此使用不同的变量
x不会影响比较或多项式:- 参数:
- x字符串,可选
“lambda”变量的名称,默认为“lambda”。
- 简化函数, 可选
用于对计算出的特征多项式进行简化的函数。默认为
simplify。
参见
注释
Samuelson-Berkowitz 算法用于高效地计算特征多项式,并且不涉及任何除法操作。因此,可以在没有零因子的任何交换环上计算特征多项式。
如果行列式 det(x*I - M) 可以像上三角矩阵或下三角矩阵那样容易地求出,那么可以借助特征值来计算特征多项式,而不是使用 Samuelson-Berkowitz 算法。
示例
>>> from sympy import Matrix >>> from sympy.abc import x, y >>> M = Matrix([[1, 3], [2, 0]]) >>> M.charpoly() PurePoly(lambda**2 - lambda - 6, lambda, domain='ZZ') >>> M.charpoly(x) == M.charpoly(y) True >>> M.charpoly(x) == M.charpoly(y) True
指定
x是可选的;默认使用名为lambda的符号(在unicode中美观打印时看起来不错):>>> M.charpoly().as_expr() lambda**2 - lambda - 6
如果
x与现有符号冲突,下划线将被添加到名称前以使其唯一:>>> M = Matrix([[1, 2], [x, 0]]) >>> M.charpoly(x).as_expr() _x**2 - _x - 2*x
无论你是否传递一个符号,生成器都可以通过 gen 属性获得,因为它可能与传递的符号不同:
>>> M.charpoly(x).gen _x >>> M.charpoly(x).gen == x False
- cholesky(hermitian=True)[源代码][源代码]¶
返回矩阵 A 的 Cholesky 类型分解 L,使得如果 hermitian 标志为 True,则 L * L.H == A,或者如果 hermitian 为 False,则 L * L.T == A。
如果 hermitian 为 True,A 必须是一个厄米正定矩阵;如果为 False,A 必须是一个对称矩阵。
参见
示例
>>> from sympy import Matrix >>> A = Matrix(((25, 15, -5), (15, 18, 0), (-5, 0, 11))) >>> A.cholesky() Matrix([ [ 5, 0, 0], [ 3, 3, 0], [-1, 1, 3]]) >>> A.cholesky() * A.cholesky().T Matrix([ [25, 15, -5], [15, 18, 0], [-5, 0, 11]])
矩阵可以有复数项:
>>> from sympy import I >>> A = Matrix(((9, 3*I), (-3*I, 5))) >>> A.cholesky() Matrix([ [ 3, 0], [-I, 2]]) >>> A.cholesky() * A.cholesky().H Matrix([ [ 9, 3*I], [-3*I, 5]])
非厄米特 Cholesky 型分解在矩阵不是正定的情况下可能是有用的。
>>> A = Matrix([[1, 2], [2, 1]]) >>> L = A.cholesky(hermitian=False) >>> L Matrix([ [1, 0], [2, sqrt(3)*I]]) >>> L*L.T == A True
- cofactor(i, j, method='berkowitz')[源代码][源代码]¶
计算元素的余子式。
- 参数:
- 方法字符串,可选
用于查找余子式的方法,可以是“bareiss”、“berkowitz”、“bird”、“laplace”或“lu”。
示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2], [3, 4]]) >>> M.cofactor(0, 1) -3
- cofactor_matrix(method='berkowitz')[源代码][源代码]¶
返回一个包含每个元素的余子式的矩阵。
- 参数:
- 方法字符串,可选
用于查找余子式的方法,可以是“bareiss”、“berkowitz”、“bird”、“laplace”或“lu”。
示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2], [3, 4]]) >>> M.cofactor_matrix() Matrix([ [ 4, -3], [-2, 1]])
- col_insert(pos, other)[源代码][源代码]¶
在给定的列位置插入一列或多列。
参见
示例
>>> from sympy import zeros, ones >>> M = zeros(3) >>> V = ones(3, 1) >>> M.col_insert(1, V) Matrix([ [0, 1, 0, 0], [0, 1, 0, 0], [0, 1, 0, 0]])
- col_join(other)[源代码][源代码]¶
将两个矩阵沿着自身的最后一行和另一个矩阵的第一行进行连接。
示例
>>> from sympy import zeros, ones >>> M = zeros(3) >>> V = ones(1, 3) >>> M.col_join(V) Matrix([ [0, 0, 0], [0, 0, 0], [0, 0, 0], [1, 1, 1]])
- columnspace(simplify=False)[源代码][源代码]¶
返回一个向量列表(矩阵对象),这些向量跨越
M的列空间示例
>>> from sympy import Matrix >>> M = Matrix(3, 3, [1, 3, 0, -2, -6, 0, 3, 9, 6]) >>> M Matrix([ [ 1, 3, 0], [-2, -6, 0], [ 3, 9, 6]]) >>> M.columnspace() [Matrix([ [ 1], [-2], [ 3]]), Matrix([ [0], [0], [6]])]
- classmethod companion(poly)[源代码][源代码]¶
返回多项式的伴随矩阵。
示例
>>> from sympy import Matrix, Poly, Symbol, symbols >>> x = Symbol('x') >>> c0, c1, c2, c3, c4 = symbols('c0:5') >>> p = Poly(c0 + c1*x + c2*x**2 + c3*x**3 + c4*x**4 + x**5, x) >>> Matrix.companion(p) Matrix([ [0, 0, 0, 0, -c0], [1, 0, 0, 0, -c1], [0, 1, 0, 0, -c2], [0, 0, 1, 0, -c3], [0, 0, 0, 1, -c4]])
- condition_number()[源代码][源代码]¶
返回矩阵的条件数。
这是最大奇异值除以最小奇异值
示例
>>> from sympy import Matrix, S >>> A = Matrix([[1, 0, 0], [0, 10, 0], [0, 0, S.One/10]]) >>> A.condition_number() 100
- conjugate()[源代码][源代码]¶
返回按元素的共轭。
参见
transpose矩阵转置
HHermite 共轭
sympy.matrices.matrixbase.MatrixBase.DDirac 共轭
示例
>>> from sympy import SparseMatrix, I >>> a = SparseMatrix(((1, 2 + I), (3, 4), (I, -I))) >>> a Matrix([ [1, 2 + I], [3, 4], [I, -I]]) >>> a.C Matrix([ [ 1, 2 - I], [ 3, 4], [-I, I]])
- connected_components()[源代码][源代码]¶
当一个方阵被视为加权图时,返回图中连接顶点的列表。
注释
即使矩阵的任何符号元素在数学上可能是不确定的零,这仅考虑了矩阵的结构方面,因此它们将被视为非零。
示例
>>> from sympy import Matrix >>> A = Matrix([ ... [66, 0, 0, 68, 0, 0, 0, 0, 67], ... [0, 55, 0, 0, 0, 0, 54, 53, 0], ... [0, 0, 0, 0, 1, 2, 0, 0, 0], ... [86, 0, 0, 88, 0, 0, 0, 0, 87], ... [0, 0, 10, 0, 11, 12, 0, 0, 0], ... [0, 0, 20, 0, 21, 22, 0, 0, 0], ... [0, 45, 0, 0, 0, 0, 44, 43, 0], ... [0, 35, 0, 0, 0, 0, 34, 33, 0], ... [76, 0, 0, 78, 0, 0, 0, 0, 77]]) >>> A.connected_components() [[0, 3, 8], [1, 6, 7], [2, 4, 5]]
- connected_components_decomposition()[源代码][源代码]¶
仅使用排列将一个方阵分解为块对角形式。
- 返回:
- P, B排列矩阵, 块对角矩阵
P 是相似变换的置换矩阵,如解释中所述。而 B 是置换结果的块对角矩阵。
如果你想从 BlockDiagMatrix 中获取对角块,请参见
get_diag_blocks()。
注释
这个问题对应于在将矩阵视为加权图时,寻找图的连通分量。
示例
>>> from sympy import Matrix, pprint >>> A = Matrix([ ... [66, 0, 0, 68, 0, 0, 0, 0, 67], ... [0, 55, 0, 0, 0, 0, 54, 53, 0], ... [0, 0, 0, 0, 1, 2, 0, 0, 0], ... [86, 0, 0, 88, 0, 0, 0, 0, 87], ... [0, 0, 10, 0, 11, 12, 0, 0, 0], ... [0, 0, 20, 0, 21, 22, 0, 0, 0], ... [0, 45, 0, 0, 0, 0, 44, 43, 0], ... [0, 35, 0, 0, 0, 0, 34, 33, 0], ... [76, 0, 0, 78, 0, 0, 0, 0, 77]])
>>> P, B = A.connected_components_decomposition() >>> pprint(P) PermutationMatrix((1 3)(2 8 5 7 4 6)) >>> pprint(B) [[66 68 67] ] [[ ] ] [[86 88 87] 0 0 ] [[ ] ] [[76 78 77] ] [ ] [ [55 54 53] ] [ [ ] ] [ 0 [45 44 43] 0 ] [ [ ] ] [ [35 34 33] ] [ ] [ [0 1 2 ]] [ [ ]] [ 0 0 [10 11 12]] [ [ ]] [ [20 21 22]]
>>> P = P.as_explicit() >>> B = B.as_explicit() >>> P.T*B*P == A True
- copy()[源代码][源代码]¶
返回矩阵的副本。
示例
>>> from sympy import Matrix >>> A = Matrix(2, 2, [1, 2, 3, 4]) >>> A.copy() Matrix([ [1, 2], [3, 4]])
- cramer_solve(rhs, det_method='laplace')[源代码][源代码]¶
使用克莱姆法则求解线性方程组。
与其他方法相比,这种方法相对低效。然而,它只使用一次除法,假设提供了一种无除法的行列式方法。这对于最小化线性系统符号解中除以零的情况很有帮助。
- 参数:
- M矩阵
表示方程左侧的矩阵。
- rhs矩阵
表示方程右侧的矩阵。
- det_method字符串或可调用对象
用于计算矩阵行列式的方法。默认是
'laplace'。如果传递了一个可调用对象,它应该接受一个参数,即矩阵,并返回该矩阵的行列式。
- 返回:
- x矩阵
满足
Ax = B的矩阵。将具有与矩阵 A 的列数相同的行数,以及与矩阵 B 相同的列数。
参考文献
示例
>>> from sympy import Matrix >>> A = Matrix([[0, -6, 1], [0, -6, -1], [-5, -2, 3]]) >>> B = Matrix([[-30, -9], [-18, -27], [-26, 46]]) >>> x = A.cramer_solve(B) >>> x Matrix([ [ 0, -5], [ 4, 3], [-6, 9]])
- cross(b)[源代码][源代码]¶
返回
self和b的叉积,放松对兼容维度的条件:如果每个都有3个元素,将返回与self类型和形状相同的矩阵。如果b与self形状相同,则叉积的常见恒等式(如 \(a imes b = - b imes a\))将成立。- 参数:
- b3x1 或 1x3 矩阵
- det(method='bareiss', iszerofunc=None)[源代码][源代码]¶
如果
M是一个具体的矩阵对象,则计算其行列式;否则,如果M是一个MatrixSymbol或其他表达式,则返回表达式Determinant(M)。- 参数:
- 方法字符串,可选
指定用于计算矩阵行列式的算法。
如果矩阵最多为3x3,则使用硬编码公式,并忽略指定的方法。否则,默认使用
'bareiss'。此外,如果矩阵是上三角矩阵或下三角矩阵,行列式通过对角元素的简单乘法计算,指定的方法将被忽略。
如果设置为
'domain-ge',则将通过使用 DomainMatrix 来使用高斯消去法。如果设置为
'bareiss',将使用 Bareiss 的无分数算法。如果设置为
'berkowitz',将使用 Berkowitz 算法。如果设置为
'bird',将使用 Bird 的算法 [1]。如果设置为
'laplace',将使用拉普拉斯算法。否则,如果设置为
'lu',将使用 LU 分解。备注
为了向后兼容,类似“bareis”和“det_lu”的遗留键仍然可以用来指示相应的方法。而且,目前这些键是不区分大小写的。然而,建议使用精确的键来指定方法。
- iszerofuncFunctionType 或 None, 可选
如果设置为
None,如果方法设置为'bareiss',则默认为_iszero,如果方法设置为'lu',则默认为_is_zero_after_expand_mul。它还可以接受任何用户指定的零测试函数,如果该函数格式化为接受单个符号参数并返回
True如果测试为零,返回False如果测试为非零,并且如果无法决定则返回None。
- 返回:
- det基本
行列式的结果。
- Raises:
- ValueError
如果为
method或iszerofunc提供了未识别的键。- NonSquareMatrixError
如果尝试从非方阵计算行列式。
参考文献
[1]Bird, R. S. (2011). 一个计算行列式的无除法简单算法。信息处理快报, 111(21), 1072-1074. doi: 10.1016/j.ipl.2011.08.006
示例
>>> from sympy import Matrix, eye, det >>> I3 = eye(3) >>> det(I3) 1 >>> M = Matrix([[1, 2], [3, 4]]) >>> det(M) -2 >>> det(M) == M.det() True >>> M.det(method="domain-ge") -2
- det_LU_decomposition()[源代码][源代码]¶
使用LU分解计算矩阵行列式。
请注意,如果LU分解本身失败,此方法将失败。特别是,如果矩阵没有逆,此方法将失败。
TODO: 实现稀疏矩阵的算法 (SFF),http://www.eecis.udel.edu/~saunders/papers/sffge/it5.ps.
参见
- classmethod diag(
- *args,
- strict=False,
- unpack=True,
- rows=None,
- cols=None,
- **kwargs,
返回一个具有指定对角线的矩阵。如果传递了矩阵,则创建一个分块对角矩阵(即矩阵的“直和”)。
示例
>>> from sympy import Matrix >>> Matrix.diag(1, 2, 3) Matrix([ [1, 0, 0], [0, 2, 0], [0, 0, 3]])
当前默认是解包单个序列。如果这不是所需的行为,请设置 \(unpack=False\),它将被解释为矩阵。
>>> Matrix.diag([1, 2, 3]) == Matrix.diag(1, 2, 3) True
当传递多个元素时,每个元素都被解释为对角线上的内容。列表被转换为矩阵。对角线的填充总是从前一个元素的右下角继续:这将创建一个分块对角矩阵,无论矩阵是否为方形。
>>> col = [1, 2, 3] >>> row = [[4, 5]] >>> Matrix.diag(col, row) Matrix([ [1, 0, 0], [2, 0, 0], [3, 0, 0], [0, 4, 5]])
当 \(unpack\) 为 False 时,列表中的元素不必全部具有相同的长度。将 \(strict\) 设置为 True 会为以下情况引发 ValueError:
>>> Matrix.diag([[1, 2, 3], [4, 5], [6]], unpack=False) Matrix([ [1, 2, 3], [4, 5, 0], [6, 0, 0]])
返回矩阵的类型可以通过
cls关键字设置。>>> from sympy import ImmutableMatrix >>> from sympy.utilities.misc import func_name >>> func_name(Matrix.diag(1, cls=ImmutableMatrix)) 'ImmutableDenseMatrix'
零维矩阵可以用来定位填充在任意行或列的开始位置:
>>> from sympy import ones >>> r2 = ones(0, 2) >>> Matrix.diag(r2, 1, 2) Matrix([ [0, 0, 1, 0], [0, 0, 0, 2]])
- diagonal(k=0)[源代码][源代码]¶
返回 self 的第 k 条对角线。主对角线对应于 \(k=0\);上方和下方的对角线分别对应于 \(k > 0\) 和 \(k < 0\)。返回 \(self[i, j]\) 的值,其中 \(j - i = k\),按 \(i + j\) 的递增顺序返回,从 \(i + j = |k|\) 开始。
参见
示例
>>> from sympy import Matrix >>> m = Matrix(3, 3, lambda i, j: j - i); m Matrix([ [ 0, 1, 2], [-1, 0, 1], [-2, -1, 0]]) >>> _.diagonal() Matrix([[0, 0, 0]]) >>> m.diagonal(1) Matrix([[1, 1]]) >>> m.diagonal(-2) Matrix([[-2]])
尽管对角线作为矩阵返回,但元素检索可以通过单个索引完成:
>>> Matrix.diag(1, 2, 3).diagonal()[1] # instead of [0, 1] 2
- diagonal_solve(rhs)[源代码][源代码]¶
高效求解
Ax = B,其中 A 是一个对角矩阵,且对角元素非零。参见
示例
>>> from sympy import Matrix, eye >>> A = eye(2)*2 >>> B = Matrix([[1, 2], [3, 4]]) >>> A.diagonal_solve(B) == B/2 True
- diagonalize(
- reals_only=False,
- sort=False,
- normalize=False,
返回 (P, D),其中 D 是对角矩阵。
D = P^-1 * M * P
其中 M 是当前矩阵。
- 参数:
- reals_onlybool. 如果需要复数时是否抛出错误
对角化。(默认值:False)
- 排序bool. 沿对角线对特征值进行排序。(默认值:False)
- 规范化bool. 如果为 True,则对 P 的列进行归一化。(默认值:False)
示例
>>> from sympy import Matrix >>> M = Matrix(3, 3, [1, 2, 0, 0, 3, 0, 2, -4, 2]) >>> M Matrix([ [1, 2, 0], [0, 3, 0], [2, -4, 2]]) >>> (P, D) = M.diagonalize() >>> D Matrix([ [1, 0, 0], [0, 2, 0], [0, 0, 3]]) >>> P Matrix([ [-1, 0, -1], [ 0, 0, -1], [ 2, 1, 2]]) >>> P.inv() * M * P Matrix([ [1, 0, 0], [0, 2, 0], [0, 0, 3]])
- diff(*args, evaluate=True, **kwargs)[源代码][源代码]¶
计算矩阵中每个元素的导数。
示例
>>> from sympy import Matrix >>> from sympy.abc import x, y >>> M = Matrix([[x, y], [1, 0]]) >>> M.diff(x) Matrix([ [1, 0], [0, 0]])
- dot(
- b,
- hermitian=None,
- conjugate_convention=None,
返回两个长度相等的向量的点积或内积。这里
self必须是一个大小为 1 x n 或 n x 1 的Matrix,而b必须是一个大小为 1 x n 或 n x 1 的矩阵,或者是一个长度为 n 的列表/元组。返回一个标量。默认情况下,
dot不会共轭self或b,即使存在复杂条目。设置hermitian=True``(并可选地设置 ``conjugate_convention)以计算厄米内积。可能的 kwargs 是
hermitian和conjugate_convention。如果
conjugate_convention是"left"、"math"或"maths",则使用第一个向量 (self) 的共轭。如果指定"right"或"physics",则使用第二个向量b的共轭。示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> v = Matrix([1, 1, 1]) >>> M.row(0).dot(v) 6 >>> M.col(0).dot(v) 12 >>> v = [3, 2, 1] >>> M.row(0).dot(v) 10
>>> from sympy import I >>> q = Matrix([1*I, 1*I, 1*I]) >>> q.dot(q, hermitian=False) -3
>>> q.dot(q, hermitian=True) 3
>>> q1 = Matrix([1, 1, 1*I]) >>> q.dot(q1, hermitian=True, conjugate_convention="maths") 1 - 2*I >>> q.dot(q1, hermitian=True, conjugate_convention="physics") 1 + 2*I
- dual()[源代码][源代码]¶
返回矩阵的对偶。
矩阵的对偶是:
(1/2)*levicivita(i, j, k, l)*M(k, l)对指标 \(k\) 和 \(l\) 求和由于levicivita方法对于任何指标的成对交换都是反对称的,对称矩阵的对偶是零矩阵。严格来说,这里定义的对偶假设矩阵 \(M\) 是一个逆变反对称二阶张量,因此对偶是一个协变二阶张量。
- echelon_form(
- iszerofunc=<function _iszero>,
- simplify=False,
- with_pivots=False,
返回一个与
M行等价的矩阵,该矩阵为阶梯形式。注意,矩阵的阶梯形式是*不*唯一的,然而,像行空间和零空间这样的性质是保持不变的。示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2], [3, 4]]) >>> M.echelon_form() Matrix([ [1, 2], [0, -2]])
- eigenvals(
- error_when_incomplete=True,
- **flags,
计算矩阵的特征值。
- 参数:
- error_when_incompletebool, 可选
如果设置为
True,如果未计算出所有特征值,则会引发错误。这是由于roots未返回完整的特征值列表所导致的。- 简化布尔值或函数,可选
如果设置为
True,它将尝试返回通过在每个例程中应用默认简化方法返回的表达式的最简化形式。如果设置为
False,它将在此特定例程中跳过简化以节省计算资源。如果传递了一个函数,它将尝试将该特定函数作为简化方法应用。
- 理性bool, 可选
如果设置为
True,每个浮点数将在计算前被替换为有理数。这可以解决roots例程在处理浮点数时的一些问题。- 多个bool, 可选
如果设置为
True,结果将以列表的形式呈现。如果设置为
False,结果将以字典的形式返回。
- 返回:
- eigs列表或字典
矩阵的特征值。返回格式将由键
multiple指定。
- Raises:
- MatrixError
如果计算的根数不足。
- NonSquareMatrixError
如果尝试从非方阵计算特征值。
注释
矩阵 \(A\) 的特征值可以通过求解矩阵方程 \(\det(A - \lambda I) = 0\) 来计算
由于 Abel-Ruffini 定理,对于形状大于 \(4, 4\) 的矩阵,并不总是能够返回特征值的激进解。
如果没有找到特征值的根本解决方案,它可能会以
sympy.polys.rootoftools.ComplexRootOf的形式返回特征值。示例
>>> from sympy import Matrix >>> M = Matrix(3, 3, [0, 1, 1, 1, 0, 0, 1, 1, 1]) >>> M.eigenvals() {-1: 1, 0: 1, 2: 1}
- eigenvects(
- error_when_incomplete=True,
- iszerofunc=<function _iszero>,
- **flags,
计算矩阵的特征向量。
- 参数:
- error_when_incompletebool, 可选
当未计算出所有特征值时引发错误。这是由于
roots未返回完整的特征值列表所导致的。- iszerofunc函数, 可选
指定一个用于
rref中的零测试函数。默认值为
_iszero,它使用 SymPy 的简单且快速的默认假设处理程序。它还可以接受任何用户指定的零测试函数,如果该函数格式化为接受单个符号参数并返回
True如果测试为零,返回False如果测试为非零,以及None如果无法决定。- 简化布尔值或函数,可选
如果
True,as_content_primitive()将被用来整理规范化过程中产生的工件。它也将被
nullspace例程使用。- 砍布尔值或正数,可选
如果矩阵包含任何浮点数,它们将被转换为有理数以进行计算,但答案将在使用 evalf 评估后返回。
chop标志传递给evalf。当chop=True时,将使用默认精度;一个数字将被解释为所需的精度级别。
- 返回:
- ret[(特征值, 重数, 特征空间), …]
包含由
eigenvals和nullspace获得的数据元组的参差不齐的列表。eigenspace是一个包含每个特征值的eigenvector的列表。eigenvector是一个以Matrix形式表示的向量。例如,一个长度为3的向量返回为Matrix([a_1, a_2, a_3])。
- Raises:
- NotImplementedError
如果计算零空间失败。
示例
>>> from sympy import Matrix >>> M = Matrix(3, 3, [0, 1, 1, 1, 0, 0, 1, 1, 1]) >>> M.eigenvects() [(-1, 1, [Matrix([ [-1], [ 1], [ 0]])]), (0, 1, [Matrix([ [ 0], [-1], [ 1]])]), (2, 1, [Matrix([ [2/3], [1/3], [ 1]])])]
- elementary_col_op(
- op='n->kn',
- col=None,
- k=None,
- col1=None,
- col2=None,
执行基本列操作 \(op\)。
\(op\) 可以是以下之一
"n->kn"(列 n 变为 k*n)"n<->m"(交换第 n 列和第 m 列)"n->n+km"(列 n 移动到列 n + k*列 m)
- 参数:
- op字符串;基本行操作
- col要应用列操作的列
- k在列操作中应用的倍数
- col1列交换中的一列
- col2列交换中的第二列或列操作中的列“m”
n->n+km
- elementary_row_op(
- op='n->kn',
- row=None,
- k=None,
- row1=None,
- row2=None,
执行基本行操作 \(op\)。
\(op\) 可以是以下之一
"n->kn"(第 n 行变为 k*n)"n<->m"(交换第 n 行和第 m 行)"n->n+km"(行 n 移动到行 n + k*行 m)
- 参数:
- op字符串;基本行操作
- 行要应用行操作的行
- k在行操作中应用的倍数
- 行1行交换的一行
- 第二行行交换的第二行或行操作中的行“m”
n->n+km
- evalf(
- n=15,
- subs=None,
- maxn=100,
- chop=False,
- strict=False,
- quad=None,
- verbose=False,
对 self 的每个元素应用 evalf()。
- exp()[源代码][源代码]¶
返回一个方阵的指数。
示例
>>> from sympy import Symbol, Matrix
>>> t = Symbol('t') >>> m = Matrix([[0, 1], [-1, 0]]) * t >>> m.exp() Matrix([ [ exp(I*t)/2 + exp(-I*t)/2, -I*exp(I*t)/2 + I*exp(-I*t)/2], [I*exp(I*t)/2 - I*exp(-I*t)/2, exp(I*t)/2 + exp(-I*t)/2]])
- expand(
- deep=True,
- modulus=None,
- power_base=True,
- power_exp=True,
- mul=True,
- log=True,
- multinomial=True,
- basic=True,
- **hints,
对矩阵的每个条目应用 core.function.expand。
示例
>>> from sympy.abc import x >>> from sympy import Matrix >>> Matrix(1, 1, [x*(x+1)]) Matrix([[x*(x + 1)]]) >>> _.expand() Matrix([[x**2 + x]])
- extract(rowsList, colsList)[源代码][源代码]¶
返回由指定行和列列表构成的子矩阵。可以给出负索引。所有索引必须在范围 \(-n \le i < n\) 内,其中 \(n\) 是行数或列数。
示例
>>> from sympy import Matrix >>> m = Matrix(4, 3, range(12)) >>> m Matrix([ [0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 10, 11]]) >>> m.extract([0, 1, 3], [0, 1]) Matrix([ [0, 1], [3, 4], [9, 10]])
行或列可以重复:
>>> m.extract([0, 0, 1], [-1]) Matrix([ [2], [2], [5]])
可以通过使用 range 来提供索引,从而获取每隔一行的数据:
>>> m.extract(range(0, m.rows, 2), [-1]) Matrix([ [2], [8]])
RowsList 或 colsList 也可以是一个布尔值列表,在这种情况下,对应于 True 值的行或列将被选中:
>>> m.extract([0, 1, 2, 3], [True, False, True]) Matrix([ [0, 2], [3, 5], [6, 8], [9, 11]])
- classmethod eye(rows, cols=None, **kwargs)[源代码][源代码]¶
返回一个单位矩阵。
- 参数:
- 行矩阵的行
- cols矩阵的列(如果为 None,则 cols=rows)
- flat()[源代码][源代码]¶
返回矩阵中所有元素的扁平列表。
示例
>>> from sympy import Matrix >>> m = Matrix([[0, 2], [3, 4]]) >>> m.flat() [0, 2, 3, 4]
- property free_symbols¶
返回矩阵中的自由符号。
示例
>>> from sympy.abc import x >>> from sympy import Matrix >>> Matrix([[x], [1]]).free_symbols {x}
- classmethod from_dok(rows, cols, dok)[源代码][源代码]¶
从键的字典创建一个矩阵。
示例
>>> from sympy import Matrix >>> d = {(0, 0): 1, (1, 2): 3, (2, 1): 4} >>> Matrix.from_dok(3, 3, d) Matrix([ [1, 0, 0], [0, 0, 3], [0, 4, 0]])
- gauss_jordan_solve(B, freevar=False)[源代码][源代码]¶
使用高斯-约旦消元法求解
Ax = B。可能没有、有一个或无限多个解。如果存在一个解,它将被返回。如果存在无限多个解,它将以参数形式返回。如果不存在解,它将抛出 ValueError。
- 参数:
- B矩阵
要解的方程的右侧。必须与矩阵A有相同的行数。
- 自由变量布尔值,可选
当设置为 \(True\) 时,标志将返回解中自由变量的索引(列矩阵),对于一个未确定的系统(例如 A 的列数多于行数),可能存在无限解,自由变量的值可以任意。默认 \(False\)。
- 返回:
- x矩阵
满足
Ax = B的矩阵。将具有与矩阵 A 的列数相同的行数,以及与矩阵 B 相同的列数。- 参数矩阵
如果系统是欠定的(例如,A 的列数多于行数),则可能存在无限多的解,这些解可以用任意参数表示。这些任意参数作为 params 矩阵返回。
- free_var_index列表,可选
如果系统是欠定的(例如,A 的列数多于行数),则可能存在无限多的解,具体取决于自由变量的任意值。然后,如果标志 \(freevar\) 设置为 \(True\),则自由变量在解(列矩阵)中的索引由 \(free_var_index\) 返回。
参见
参考文献
示例
>>> from sympy import Matrix >>> A = Matrix([[1, 2, 1, 1], [1, 2, 2, -1], [2, 4, 0, 6]]) >>> B = Matrix([7, 12, 4]) >>> sol, params = A.gauss_jordan_solve(B) >>> sol Matrix([ [-2*tau0 - 3*tau1 + 2], [ tau0], [ 2*tau1 + 5], [ tau1]]) >>> params Matrix([ [tau0], [tau1]]) >>> taus_zeroes = { tau:0 for tau in params } >>> sol_unique = sol.xreplace(taus_zeroes) >>> sol_unique Matrix([ [2], [0], [5], [0]])
>>> A = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 10]]) >>> B = Matrix([3, 6, 9]) >>> sol, params = A.gauss_jordan_solve(B) >>> sol Matrix([ [-1], [ 2], [ 0]]) >>> params Matrix(0, 1, [])
>>> A = Matrix([[2, -7], [-1, 4]]) >>> B = Matrix([[-21, 3], [12, -2]]) >>> sol, params = A.gauss_jordan_solve(B) >>> sol Matrix([ [0, -2], [3, -1]]) >>> params Matrix(0, 2, [])
>>> from sympy import Matrix >>> A = Matrix([[1, 2, 1, 1], [1, 2, 2, -1], [2, 4, 0, 6]]) >>> B = Matrix([7, 12, 4]) >>> sol, params, freevars = A.gauss_jordan_solve(B, freevar=True) >>> sol Matrix([ [-2*tau0 - 3*tau1 + 2], [ tau0], [ 2*tau1 + 5], [ tau1]]) >>> params Matrix([ [tau0], [tau1]]) >>> freevars [1, 3]
- get_diag_blocks()[源代码][源代码]¶
获取方阵主对角线上的子方阵。
适用于反转符号矩阵或求解线性方程组,这些方程组可能通过具有块对角结构而解耦。
示例
>>> from sympy import Matrix >>> from sympy.abc import x, y, z >>> A = Matrix([[1, 3, 0, 0], [y, z*z, 0, 0], [0, 0, x, 0], [0, 0, 0, 0]]) >>> a1, a2, a3 = A.get_diag_blocks() >>> a1 Matrix([ [1, 3], [y, z**2]]) >>> a2 Matrix([[x]]) >>> a3 Matrix([[0]])
- has(*patterns)[源代码][源代码]¶
测试是否有任何子表达式匹配任何模式。
示例
>>> from sympy import Matrix, SparseMatrix, Float >>> from sympy.abc import x, y >>> A = Matrix(((1, x), (0.2, 3))) >>> B = SparseMatrix(((1, x), (0.2, 3))) >>> A.has(x) True >>> A.has(y) False >>> A.has(Float) True >>> B.has(x) True >>> B.has(y) False >>> B.has(Float) True
- hat()[源代码][源代码]¶
返回表示叉积的反对称矩阵,使得
self.hat() * b等价于self.cross(b)。示例
调用
hat会从 3x1 矩阵创建一个反对称的 3x3 矩阵:>>> from sympy import Matrix >>> a = Matrix([1, 2, 3]) >>> a.hat() Matrix([ [ 0, -3, 2], [ 3, 0, -1], [-2, 1, 0]])
将其与另一个 3x1 矩阵相乘计算叉积:
>>> b = Matrix([3, 2, 1]) >>> a.hat() * b Matrix([ [-4], [ 8], [-4]])
这等同于调用
cross方法:>>> a.cross(b) Matrix([ [-4], [ 8], [-4]])
- classmethod hstack(*args)[源代码][源代码]¶
返回一个矩阵,该矩阵通过水平连接参数(即通过重复应用 row_join)形成。
示例
>>> from sympy import Matrix, eye >>> Matrix.hstack(eye(2), 2*eye(2)) Matrix([ [1, 0, 2, 0], [0, 1, 0, 2]])
- integrate(*args, **kwargs)[源代码][源代码]¶
对矩阵的每个元素进行积分。
args将被传递给integrate函数。示例
>>> from sympy import Matrix >>> from sympy.abc import x, y >>> M = Matrix([[x, y], [1, 0]]) >>> M.integrate((x, )) Matrix([ [x**2/2, x*y], [ x, 0]]) >>> M.integrate((x, 0, 2)) Matrix([ [2, 2*y], [2, 0]])
- inv(
- method=None,
- iszerofunc=<function _iszero>,
- try_block_diag=False,
使用指定方法返回矩阵的逆。默认情况下,如果找到合适的域,则为 DM,否则对于密集矩阵为 GE,对于稀疏矩阵为 LDL。
- 参数:
- 方法(‘DM’, ‘DMNC’, ‘GE’, ‘LU’, ‘ADJ’, ‘CH’, ‘LDL’, ‘QR’)
- iszerofunc函数, 可选
零测试功能可供使用。
- try_block_diagbool, 可选
如果为真,则将尝试使用 get_diag_blocks() 方法形成块对角矩阵,分别求逆这些矩阵,然后重建完整的逆矩阵。
- Raises:
- ValueError
如果矩阵的行列式为零。
注释
根据
method关键字,它调用适当的方法:DM …. 使用 DomainMatrix
inv_den方法 DMNC …. 使用 DomainMatrixinv_den方法而不进行消去 GE …. inverse_GE(); 密集矩阵的默认方法 LU …. inverse_LU() ADJ … inverse_ADJ() CH … inverse_CH() LDL … inverse_LDL(); 稀疏矩阵的默认方法 QR … inverse_QR()注意,GE 和 LU 方法可能需要在矩阵被求逆之前进行简化,以便在选主元过程中正确检测零。在困难的情况下,可以通过将
iszerofunc参数设置为一个函数来提供自定义的零检测函数,该函数应在参数为零时返回 True。ADJ 例程计算行列式,并使用该行列式来检测奇异矩阵,除了测试对角线上的零之外。示例
>>> from sympy import SparseMatrix, Matrix >>> A = SparseMatrix([ ... [ 2, -1, 0], ... [-1, 2, -1], ... [ 0, 0, 2]]) >>> A.inv('CH') Matrix([ [2/3, 1/3, 1/6], [1/3, 2/3, 1/3], [ 0, 0, 1/2]]) >>> A.inv(method='LDL') # use of 'method=' is optional Matrix([ [2/3, 1/3, 1/6], [1/3, 2/3, 1/3], [ 0, 0, 1/2]]) >>> A * _ Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]]) >>> A = Matrix(A) >>> A.inv('CH') Matrix([ [2/3, 1/3, 1/6], [1/3, 2/3, 1/3], [ 0, 0, 1/2]]) >>> A.inv('ADJ') == A.inv('GE') == A.inv('LU') == A.inv('CH') == A.inv('LDL') == A.inv('QR') True
- classmethod irregular(ntop, *matrices, **kwargs)[源代码][源代码]¶
返回一个由给定矩阵填充的矩阵,这些矩阵按从左到右、从上到下的顺序依次出现,并首次出现在矩阵中。它们必须完全填充矩阵。
示例
>>> from sympy import ones, Matrix >>> Matrix.irregular(3, ones(2,1), ones(3,3)*2, ones(2,2)*3, ... ones(1,1)*4, ones(2,2)*5, ones(1,2)*6, ones(1,2)*7) Matrix([ [1, 2, 2, 2, 3, 3], [1, 2, 2, 2, 3, 3], [4, 2, 2, 2, 5, 5], [6, 6, 7, 7, 5, 5]])
- is_anti_symmetric(simplify=True)[源代码][源代码]¶
检查矩阵 M 是否为反对称矩阵,即,M 是一个方阵,且所有 M[i, j] == -M[j, i]。
当
simplify=True(默认)时,在测试是否为零之前,先对 M[i, j] + M[j, i] 进行简化。默认情况下,使用 SymPy 的简化函数。要使用自定义函数,请将 simplify 设置为一个接受单个参数并返回简化表达式的函数。要跳过简化,请将 simplify 设置为 False,但请注意,虽然这会更快,但可能会导致误报。示例
>>> from sympy import Matrix, symbols >>> m = Matrix(2, 2, [0, 1, -1, 0]) >>> m Matrix([ [ 0, 1], [-1, 0]]) >>> m.is_anti_symmetric() True >>> x, y = symbols('x y') >>> m = Matrix(2, 3, [0, 0, x, -y, 0, 0]) >>> m Matrix([ [ 0, 0, x], [-y, 0, 0]]) >>> m.is_anti_symmetric() False
>>> from sympy.abc import x, y >>> m = Matrix(3, 3, [0, x**2 + 2*x + 1, y, ... -(x + 1)**2, 0, x*y, ... -y, -x*y, 0])
默认情况下,矩阵元素的简化是进行的,因此即使两个本应相等且相反的元素不会通过相等性测试,矩阵仍被报告为反对称:
>>> m[0, 1] == -m[1, 0] False >>> m.is_anti_symmetric() True
如果在矩阵已经简化的情况下使用
simplify=False,这将加快处理速度。在这里,我们看到在不进行简化的情况下,矩阵并不表现出反对称性:>>> print(m.is_anti_symmetric(simplify=False)) None
但如果矩阵已经展开,那么它将呈现反对称性,并且在 is_anti_symmetric 例程中不需要简化:
>>> m = m.expand() >>> m.is_anti_symmetric(simplify=False) True
- is_diagonal()[源代码][源代码]¶
检查矩阵是否为对角矩阵,即主对角线以外的所有元素均为零的矩阵。
示例
>>> from sympy import Matrix, diag >>> m = Matrix(2, 2, [1, 0, 0, 2]) >>> m Matrix([ [1, 0], [0, 2]]) >>> m.is_diagonal() True
>>> m = Matrix(2, 2, [1, 1, 0, 2]) >>> m Matrix([ [1, 1], [0, 2]]) >>> m.is_diagonal() False
>>> m = diag(1, 2, 3) >>> m Matrix([ [1, 0, 0], [0, 2, 0], [0, 0, 3]]) >>> m.is_diagonal() True
- is_diagonalizable(
- reals_only=False,
- **kwargs,
如果矩阵可对角化,则返回
True。- 参数:
- reals_onlybool, 可选
如果
True,它会测试矩阵是否可以对角化,使得对角线上的元素仅为实数。如果
False,它会测试矩阵是否可以对角化,即使可能涉及非实数的数值。
示例
可对角化矩阵的例子:
>>> from sympy import Matrix >>> M = Matrix([[1, 2, 0], [0, 3, 0], [2, -4, 2]]) >>> M.is_diagonalizable() True
不可对角化矩阵的示例:
>>> M = Matrix([[0, 1], [0, 0]]) >>> M.is_diagonalizable() False
以非实数项对角化的矩阵示例:
>>> M = Matrix([[0, 1], [-1, 0]]) >>> M.is_diagonalizable(reals_only=False) True >>> M.is_diagonalizable(reals_only=True) False
- property is_echelon¶
如果矩阵是阶梯形式,则返回 \(True\)。也就是说,所有零行都在底部,并且在每一行的前导非零元素下方都是零。
- property is_hermitian¶
检查矩阵是否为厄米矩阵。
在厄米矩阵中,元素 i,j 是元素 j,i 的复共轭。
示例
>>> from sympy import Matrix >>> from sympy import I >>> from sympy.abc import x >>> a = Matrix([[1, I], [-I, 1]]) >>> a Matrix([ [ 1, I], [-I, 1]]) >>> a.is_hermitian True >>> a[0, 0] = 2*I >>> a.is_hermitian False >>> a[0, 0] = x >>> a.is_hermitian >>> a[0, 1] = a[1, 0]*I >>> a.is_hermitian False
- property is_indefinite¶
找出矩阵的确定性。
注释
尽管有些人认为正定矩阵的定义仅限于对称或厄米特矩阵,但这种限制是不正确的,因为它没有根据定义 \(x^T A x > 0\) 或 \(\text{re}(x^H A x) > 0\) 对所有正定矩阵进行分类。
例如,上面例子中的
Matrix([[1, 2], [-2, 1]])是一个非对称实正定矩阵的例子。然而,由于以下公式成立;
\[\text{re}(x^H A x) > 0 \iff \text{re}(x^H \frac{A + A^H}{2} x) > 0\]我们可以通过将矩阵转换为 \(\frac{A + A^T}{2}\) 或 \(\frac{A + A^H}{2}\)(这保证始终是实对称或复埃尔米特)来分类所有可能是或不是对称或埃尔米特的正定矩阵,并且我们可以将大部分研究推迟到对称或埃尔米特正定矩阵。
但对于 Cholesky 分解的存在性,这是一个不同的问题。因为即使一个非对称或非厄米矩阵可以是正定的,Cholesky 或 LDL 分解也不存在,因为这些分解要求矩阵是对称或厄米的。
参考文献
[2]https://mathworld.wolfram.com/正定矩阵.html
[3]Johnson, C. R. “正定矩阵。” 美国数学月刊 77, 259-264 1970.
示例
对称正定矩阵的一个例子:
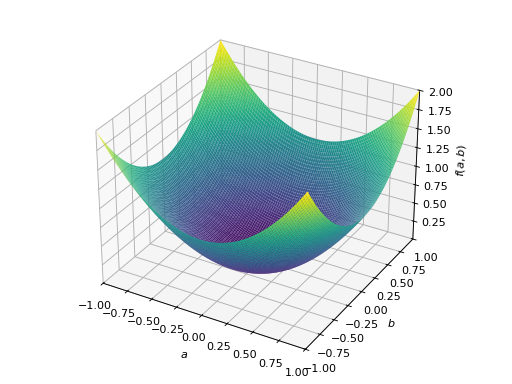
>>> from sympy import Matrix, symbols >>> from sympy.plotting import plot3d >>> a, b = symbols('a b') >>> x = Matrix([a, b])
>>> A = Matrix([[1, 0], [0, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
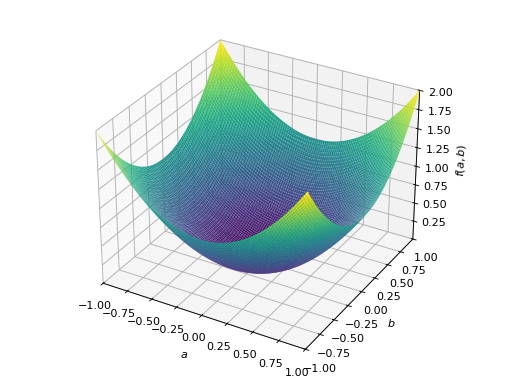
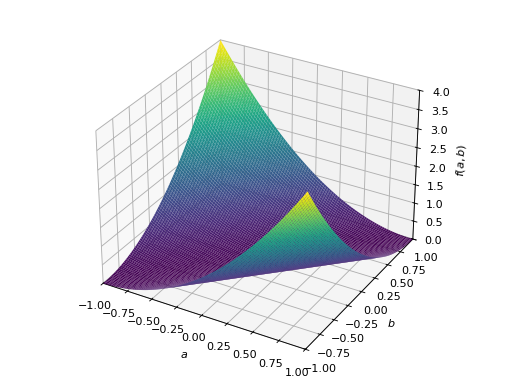
对称半正定矩阵的一个例子:
>>> A = Matrix([[1, -1], [-1, 1]]) >>> A.is_positive_definite False >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
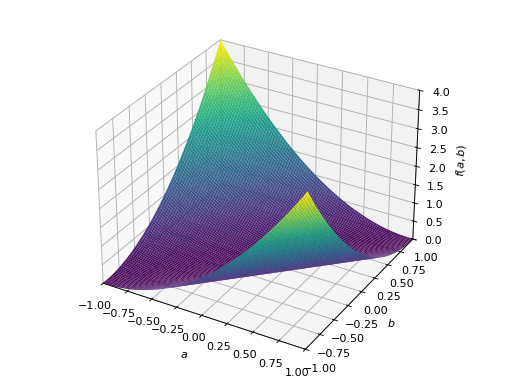
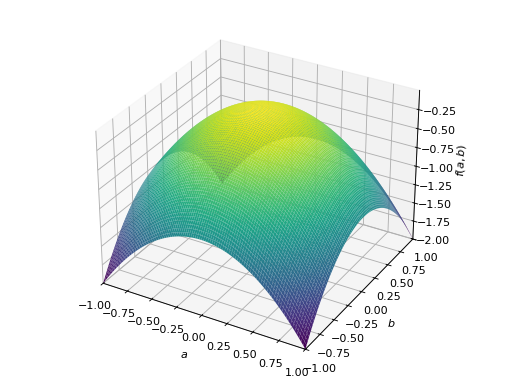
对称负定矩阵的一个例子:
>>> A = Matrix([[-1, 0], [0, -1]]) >>> A.is_negative_definite True >>> A.is_negative_semidefinite True >>> A.is_indefinite False
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
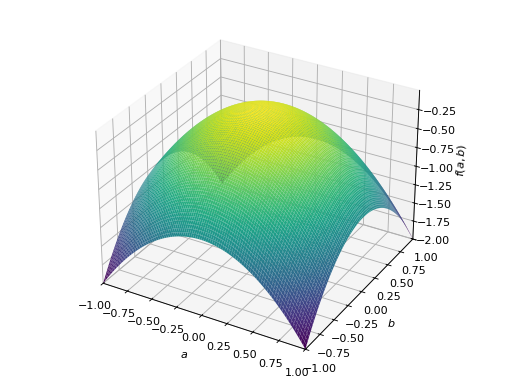
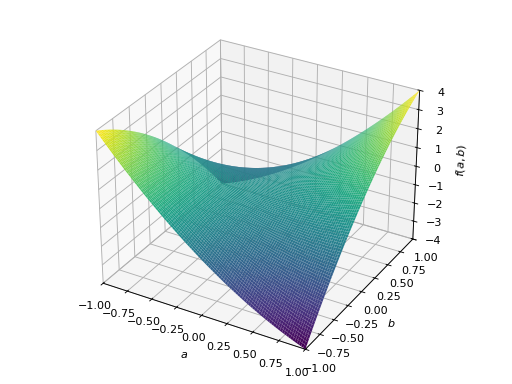
对称不定矩阵的一个例子:
>>> A = Matrix([[1, 2], [2, -1]]) >>> A.is_indefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
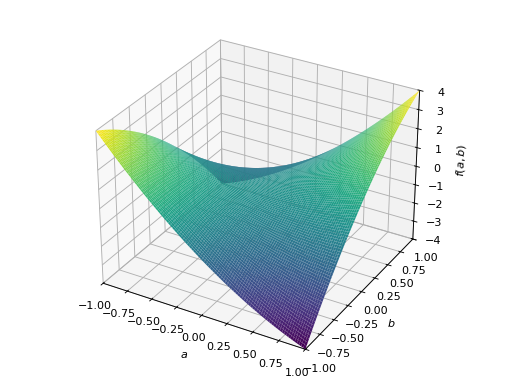
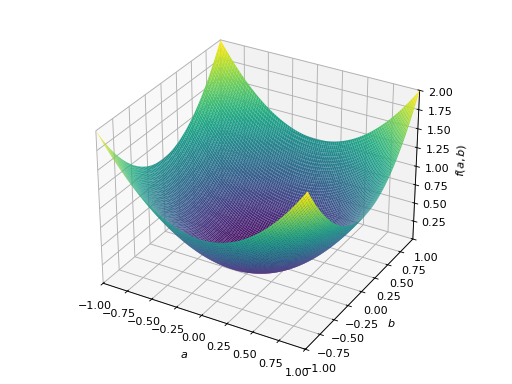
非对称正定矩阵的一个例子。
>>> A = Matrix([[1, 2], [-2, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
- property is_lower¶
检查矩阵是否为下三角矩阵。即使矩阵不是方阵,也可以返回 True。
示例
>>> from sympy import Matrix >>> m = Matrix(2, 2, [1, 0, 0, 1]) >>> m Matrix([ [1, 0], [0, 1]]) >>> m.is_lower True
>>> m = Matrix(4, 3, [0, 0, 0, 2, 0, 0, 1, 4, 0, 6, 6, 5]) >>> m Matrix([ [0, 0, 0], [2, 0, 0], [1, 4, 0], [6, 6, 5]]) >>> m.is_lower True
>>> from sympy.abc import x, y >>> m = Matrix(2, 2, [x**2 + y, y**2 + x, 0, x + y]) >>> m Matrix([ [x**2 + y, x + y**2], [ 0, x + y]]) >>> m.is_lower False
- property is_lower_hessenberg¶
检查矩阵是否为下Hessenberg形式。
下Hessenberg矩阵在其第一上对角线以上的元素为零。
示例
>>> from sympy import Matrix >>> a = Matrix([[1, 2, 0, 0], [5, 2, 3, 0], [3, 4, 3, 7], [5, 6, 1, 1]]) >>> a Matrix([ [1, 2, 0, 0], [5, 2, 3, 0], [3, 4, 3, 7], [5, 6, 1, 1]]) >>> a.is_lower_hessenberg True
- property is_negative_definite¶
找出矩阵的确定性。
注释
尽管有些人认为正定矩阵的定义仅限于对称或厄米特矩阵,但这种限制是不正确的,因为它没有根据定义 \(x^T A x > 0\) 或 \(\text{re}(x^H A x) > 0\) 对所有正定矩阵进行分类。
例如,上面例子中的
Matrix([[1, 2], [-2, 1]])是一个非对称实正定矩阵的例子。然而,由于以下公式成立;
\[\text{re}(x^H A x) > 0 \iff \text{re}(x^H \frac{A + A^H}{2} x) > 0\]我们可以通过将矩阵转换为 \(\frac{A + A^T}{2}\) 或 \(\frac{A + A^H}{2}\)(这保证始终是实对称或复埃尔米特)来分类所有可能是或不是对称或埃尔米特的正定矩阵,并且我们可以将大部分研究推迟到对称或埃尔米特正定矩阵。
但对于 Cholesky 分解的存在性,这是一个不同的问题。因为即使一个非对称或非厄米矩阵可以是正定的,Cholesky 或 LDL 分解也不存在,因为这些分解要求矩阵是对称或厄米的。
参考文献
[2]https://mathworld.wolfram.com/正定矩阵.html
[3]Johnson, C. R. “正定矩阵。” 美国数学月刊 77, 259-264 1970.
示例
对称正定矩阵的一个例子:
>>> from sympy import Matrix, symbols >>> from sympy.plotting import plot3d >>> a, b = symbols('a b') >>> x = Matrix([a, b])
>>> A = Matrix([[1, 0], [0, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
对称半正定矩阵的一个例子:
>>> A = Matrix([[1, -1], [-1, 1]]) >>> A.is_positive_definite False >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
对称负定矩阵的一个例子:
>>> A = Matrix([[-1, 0], [0, -1]]) >>> A.is_negative_definite True >>> A.is_negative_semidefinite True >>> A.is_indefinite False
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
对称不定矩阵的一个例子:
>>> A = Matrix([[1, 2], [2, -1]]) >>> A.is_indefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
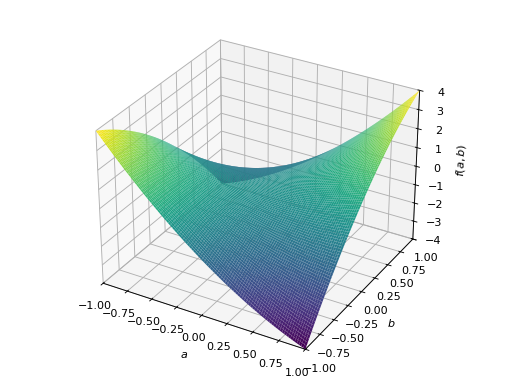
非对称正定矩阵的一个例子。
>>> A = Matrix([[1, 2], [-2, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
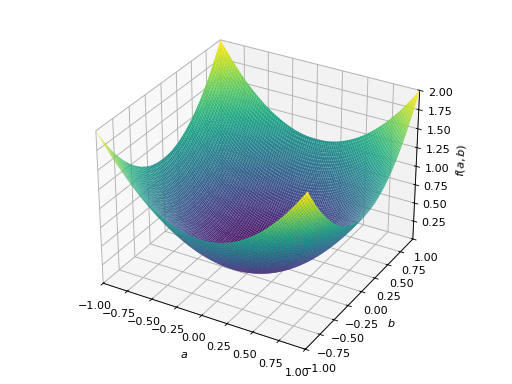
- property is_negative_semidefinite¶
找出矩阵的确定性。
注释
尽管有些人认为正定矩阵的定义仅限于对称或厄米特矩阵,但这种限制是不正确的,因为它没有根据定义 \(x^T A x > 0\) 或 \(\text{re}(x^H A x) > 0\) 对所有正定矩阵进行分类。
例如,上面例子中的
Matrix([[1, 2], [-2, 1]])是一个非对称实正定矩阵的例子。然而,由于以下公式成立;
\[\text{re}(x^H A x) > 0 \iff \text{re}(x^H \frac{A + A^H}{2} x) > 0\]我们可以通过将矩阵转换为 \(\frac{A + A^T}{2}\) 或 \(\frac{A + A^H}{2}\)(这保证始终是实对称或复埃尔米特)来分类所有可能是或不是对称或埃尔米特的正定矩阵,并且我们可以将大部分研究推迟到对称或埃尔米特正定矩阵。
但对于 Cholesky 分解的存在性,这是一个不同的问题。因为即使一个非对称或非厄米矩阵可以是正定的,Cholesky 或 LDL 分解也不存在,因为这些分解要求矩阵是对称或厄米的。
参考文献
[2]https://mathworld.wolfram.com/正定矩阵.html
[3]Johnson, C. R. “正定矩阵。” 美国数学月刊 77, 259-264 1970.
示例
对称正定矩阵的一个例子:
>>> from sympy import Matrix, symbols >>> from sympy.plotting import plot3d >>> a, b = symbols('a b') >>> x = Matrix([a, b])
>>> A = Matrix([[1, 0], [0, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
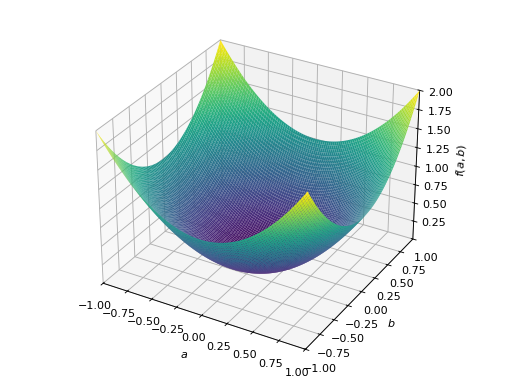
对称半正定矩阵的一个例子:
>>> A = Matrix([[1, -1], [-1, 1]]) >>> A.is_positive_definite False >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
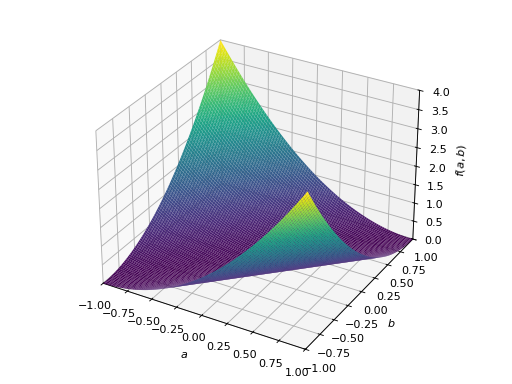
对称负定矩阵的一个例子:
>>> A = Matrix([[-1, 0], [0, -1]]) >>> A.is_negative_definite True >>> A.is_negative_semidefinite True >>> A.is_indefinite False
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
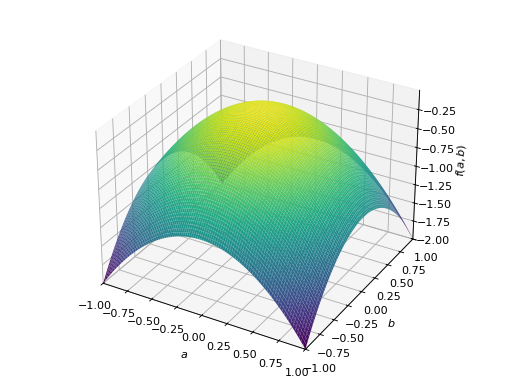
对称不定矩阵的一个例子:
>>> A = Matrix([[1, 2], [2, -1]]) >>> A.is_indefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
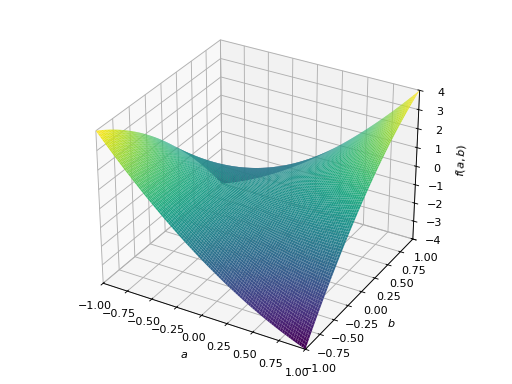
非对称正定矩阵的一个例子。
>>> A = Matrix([[1, 2], [-2, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
- is_nilpotent()[源代码][源代码]¶
检查矩阵是否为幂零矩阵。
如果对于某个整数 k,矩阵 B 的 k 次方 B**k 是一个零矩阵,则称矩阵 B 为幂零矩阵。
示例
>>> from sympy import Matrix >>> a = Matrix([[0, 0, 0], [1, 0, 0], [1, 1, 0]]) >>> a.is_nilpotent() True
>>> a = Matrix([[1, 0, 1], [1, 0, 0], [1, 1, 0]]) >>> a.is_nilpotent() False
- property is_positive_definite¶
找出矩阵的确定性。
注释
尽管有些人认为正定矩阵的定义仅限于对称或厄米特矩阵,但这种限制是不正确的,因为它没有根据定义 \(x^T A x > 0\) 或 \(\text{re}(x^H A x) > 0\) 对所有正定矩阵进行分类。
例如,上面例子中的
Matrix([[1, 2], [-2, 1]])是一个非对称实正定矩阵的例子。然而,由于以下公式成立;
\[\text{re}(x^H A x) > 0 \iff \text{re}(x^H \frac{A + A^H}{2} x) > 0\]我们可以通过将矩阵转换为 \(\frac{A + A^T}{2}\) 或 \(\frac{A + A^H}{2}\)(这保证始终是实对称或复埃尔米特)来分类所有可能是或不是对称或埃尔米特的正定矩阵,并且我们可以将大部分研究推迟到对称或埃尔米特正定矩阵。
但对于 Cholesky 分解的存在性,这是一个不同的问题。因为即使一个非对称或非厄米矩阵可以是正定的,Cholesky 或 LDL 分解也不存在,因为这些分解要求矩阵是对称或厄米的。
参考文献
[2]https://mathworld.wolfram.com/正定矩阵.html
[3]Johnson, C. R. “正定矩阵。” 美国数学月刊 77, 259-264 1970.
示例
对称正定矩阵的一个例子:
>>> from sympy import Matrix, symbols >>> from sympy.plotting import plot3d >>> a, b = symbols('a b') >>> x = Matrix([a, b])
>>> A = Matrix([[1, 0], [0, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
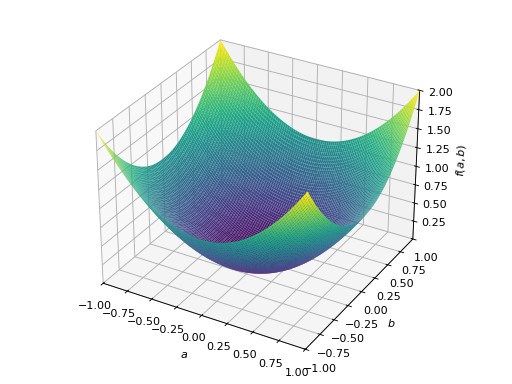
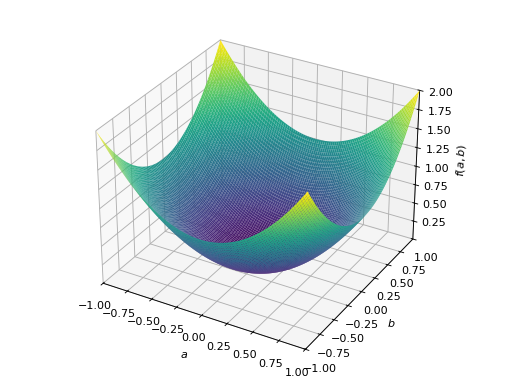
对称半正定矩阵的一个例子:
>>> A = Matrix([[1, -1], [-1, 1]]) >>> A.is_positive_definite False >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
对称负定矩阵的一个例子:
>>> A = Matrix([[-1, 0], [0, -1]]) >>> A.is_negative_definite True >>> A.is_negative_semidefinite True >>> A.is_indefinite False
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
对称不定矩阵的一个例子:
>>> A = Matrix([[1, 2], [2, -1]]) >>> A.is_indefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
非对称正定矩阵的一个例子。
>>> A = Matrix([[1, 2], [-2, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
- property is_positive_semidefinite¶
找出矩阵的确定性。
注释
尽管有些人认为正定矩阵的定义仅限于对称或厄米特矩阵,但这种限制是不正确的,因为它没有根据定义 \(x^T A x > 0\) 或 \(\text{re}(x^H A x) > 0\) 对所有正定矩阵进行分类。
例如,上面例子中的
Matrix([[1, 2], [-2, 1]])是一个非对称实正定矩阵的例子。然而,由于以下公式成立;
\[\text{re}(x^H A x) > 0 \iff \text{re}(x^H \frac{A + A^H}{2} x) > 0\]我们可以通过将矩阵转换为 \(\frac{A + A^T}{2}\) 或 \(\frac{A + A^H}{2}\)(这保证始终是实对称或复埃尔米特)来分类所有可能是或不是对称或埃尔米特的正定矩阵,并且我们可以将大部分研究推迟到对称或埃尔米特正定矩阵。
但对于 Cholesky 分解的存在性,这是一个不同的问题。因为即使一个非对称或非厄米矩阵可以是正定的,Cholesky 或 LDL 分解也不存在,因为这些分解要求矩阵是对称或厄米的。
参考文献
[2]https://mathworld.wolfram.com/正定矩阵.html
[3]Johnson, C. R. “正定矩阵。” 美国数学月刊 77, 259-264 1970.
示例
对称正定矩阵的一个例子:
>>> from sympy import Matrix, symbols >>> from sympy.plotting import plot3d >>> a, b = symbols('a b') >>> x = Matrix([a, b])
>>> A = Matrix([[1, 0], [0, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
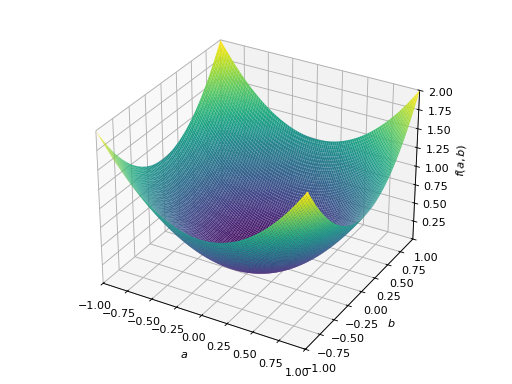
对称半正定矩阵的一个例子:
>>> A = Matrix([[1, -1], [-1, 1]]) >>> A.is_positive_definite False >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
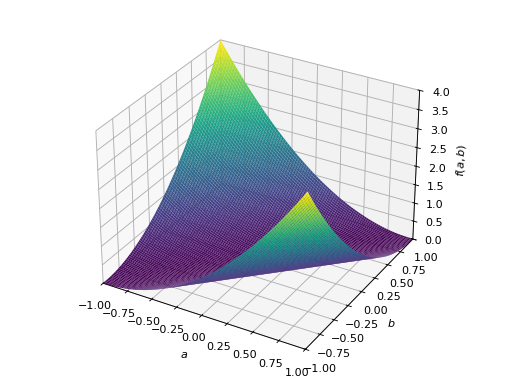
对称负定矩阵的一个例子:
>>> A = Matrix([[-1, 0], [0, -1]]) >>> A.is_negative_definite True >>> A.is_negative_semidefinite True >>> A.is_indefinite False
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
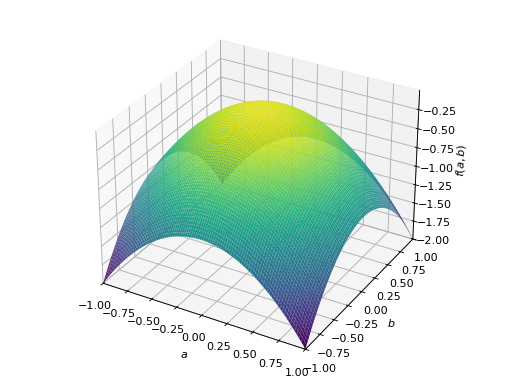
对称不定矩阵的一个例子:
>>> A = Matrix([[1, 2], [2, -1]]) >>> A.is_indefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
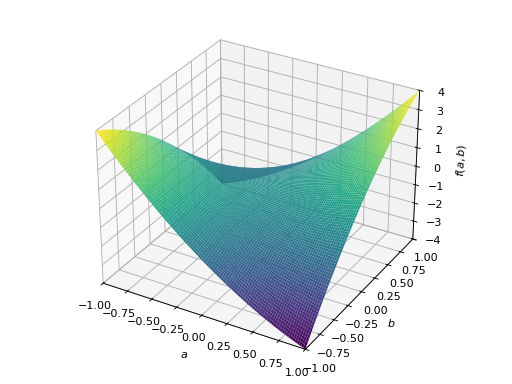
非对称正定矩阵的一个例子。
>>> A = Matrix([[1, 2], [-2, 1]]) >>> A.is_positive_definite True >>> A.is_positive_semidefinite True
>>> p = plot3d((x.T*A*x)[0, 0], (a, -1, 1), (b, -1, 1))
- property is_square¶
检查矩阵是否为方阵。
如果矩阵的行数等于列数,则该矩阵是方阵。根据定义,空矩阵是方阵,因为行数和列数均为零。
示例
>>> from sympy import Matrix >>> a = Matrix([[1, 2, 3], [4, 5, 6]]) >>> b = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> c = Matrix([]) >>> a.is_square False >>> b.is_square True >>> c.is_square True
- property is_strongly_diagonally_dominant¶
测试矩阵是否为行强对角占优。
注释
如果你想测试一个矩阵是否是列对角占优的,你可以在转置矩阵后应用测试。
示例
>>> from sympy import Matrix >>> A = Matrix([[3, -2, 1], [1, -3, 2], [-1, 2, 4]]) >>> A.is_strongly_diagonally_dominant False
>>> A = Matrix([[-2, 2, 1], [1, 3, 2], [1, -2, 0]]) >>> A.is_strongly_diagonally_dominant False
>>> A = Matrix([[-4, 2, 1], [1, 6, 2], [1, -2, 5]]) >>> A.is_strongly_diagonally_dominant True
- is_symbolic()[源代码][源代码]¶
检查是否有元素包含符号。
示例
>>> from sympy import Matrix >>> from sympy.abc import x, y >>> M = Matrix([[x, y], [1, 0]]) >>> M.is_symbolic() True
- is_symmetric(simplify=True)[源代码][源代码]¶
检查矩阵是否为对称矩阵,即方阵且等于其转置矩阵。
默认情况下,简化操作在测试对称性之前进行。可以通过使用 ‘simplify=False’ 来跳过简化;虽然这样可以稍微加快处理速度,但可能会导致误报。
示例
>>> from sympy import Matrix >>> m = Matrix(2, 2, [0, 1, 1, 2]) >>> m Matrix([ [0, 1], [1, 2]]) >>> m.is_symmetric() True
>>> m = Matrix(2, 2, [0, 1, 2, 0]) >>> m Matrix([ [0, 1], [2, 0]]) >>> m.is_symmetric() False
>>> m = Matrix(2, 3, [0, 0, 0, 0, 0, 0]) >>> m Matrix([ [0, 0, 0], [0, 0, 0]]) >>> m.is_symmetric() False
>>> from sympy.abc import x, y >>> m = Matrix(3, 3, [1, x**2 + 2*x + 1, y, (x + 1)**2, 2, 0, y, 0, 3]) >>> m Matrix([ [ 1, x**2 + 2*x + 1, y], [(x + 1)**2, 2, 0], [ y, 0, 3]]) >>> m.is_symmetric() True
如果矩阵已经简化,您可以通过使用 ‘simplify=False’ 来加速 is_symmetric() 测试。
>>> bool(m.is_symmetric(simplify=False)) False >>> m1 = m.expand() >>> m1.is_symmetric(simplify=False) True
- property is_upper¶
检查矩阵是否为上三角矩阵。即使矩阵不是方阵,也可以返回 True。
示例
>>> from sympy import Matrix >>> m = Matrix(2, 2, [1, 0, 0, 1]) >>> m Matrix([ [1, 0], [0, 1]]) >>> m.is_upper True
>>> m = Matrix(4, 3, [5, 1, 9, 0, 4, 6, 0, 0, 5, 0, 0, 0]) >>> m Matrix([ [5, 1, 9], [0, 4, 6], [0, 0, 5], [0, 0, 0]]) >>> m.is_upper True
>>> m = Matrix(2, 3, [4, 2, 5, 6, 1, 1]) >>> m Matrix([ [4, 2, 5], [6, 1, 1]]) >>> m.is_upper False
- property is_upper_hessenberg¶
检查矩阵是否为上Hessenberg形式。
上Hessenberg矩阵在第一子对角线下方有零元素。
示例
>>> from sympy import Matrix >>> a = Matrix([[1, 4, 2, 3], [3, 4, 1, 7], [0, 2, 3, 4], [0, 0, 1, 3]]) >>> a Matrix([ [1, 4, 2, 3], [3, 4, 1, 7], [0, 2, 3, 4], [0, 0, 1, 3]]) >>> a.is_upper_hessenberg True
- property is_weakly_diagonally_dominant¶
测试矩阵是否为行弱对角占优。
注释
如果你想测试一个矩阵是否是列对角占优的,你可以在转置矩阵后应用测试。
示例
>>> from sympy import Matrix >>> A = Matrix([[3, -2, 1], [1, -3, 2], [-1, 2, 4]]) >>> A.is_weakly_diagonally_dominant True
>>> A = Matrix([[-2, 2, 1], [1, 3, 2], [1, -2, 0]]) >>> A.is_weakly_diagonally_dominant False
>>> A = Matrix([[-4, 2, 1], [1, 6, 2], [1, -2, 5]]) >>> A.is_weakly_diagonally_dominant True
- property is_zero_matrix¶
检查一个矩阵是否为零矩阵。
如果矩阵的每个元素都是零,则该矩阵为零。矩阵不必是方阵即可被视为零。根据空洞真理原则,空矩阵是零。对于可能是零也可能不是零的矩阵(例如包含符号),这将返回 None。
示例
>>> from sympy import Matrix, zeros >>> from sympy.abc import x >>> a = Matrix([[0, 0], [0, 0]]) >>> b = zeros(3, 4) >>> c = Matrix([[0, 1], [0, 0]]) >>> d = Matrix([]) >>> e = Matrix([[x, 0], [0, 0]]) >>> a.is_zero_matrix True >>> b.is_zero_matrix True >>> c.is_zero_matrix False >>> d.is_zero_matrix True >>> e.is_zero_matrix
- iter_items()[源代码][源代码]¶
遍历非零项的索引和值。
参见
示例
>>> from sympy import Matrix >>> m = Matrix([[0, 1], [2, 3]]) >>> list(m.iter_items()) [((0, 1), 1), ((1, 0), 2), ((1, 1), 3)]
- iter_values()[源代码][源代码]¶
遍历 self 的非零值
参见
示例
>>> from sympy import Matrix >>> m = Matrix([[0, 1], [2, 3]]) >>> list(m.iter_values()) [1, 2, 3]
- jacobian(X)[源代码][源代码]¶
计算雅可比矩阵(向量值函数的导数)。
- 参数:
- ``self``表示函数 f_i(x_1, …, x_n) 的表达式向量。
- X按顺序排列的 x_i 集合,它可以是一个列表或一个矩阵
- ``self`` 和 X 都可以是任意顺序的行矩阵或列矩阵
- (即,jacobian() 应该始终有效)。
参见
hessianwronskian
示例
>>> from sympy import sin, cos, Matrix >>> from sympy.abc import rho, phi >>> X = Matrix([rho*cos(phi), rho*sin(phi), rho**2]) >>> Y = Matrix([rho, phi]) >>> X.jacobian(Y) Matrix([ [cos(phi), -rho*sin(phi)], [sin(phi), rho*cos(phi)], [ 2*rho, 0]]) >>> X = Matrix([rho*cos(phi), rho*sin(phi)]) >>> X.jacobian(Y) Matrix([ [cos(phi), -rho*sin(phi)], [sin(phi), rho*cos(phi)]])
- classmethod jordan_block(
- size=None,
- eigenvalue=None,
- *,
- band='upper',
- **kwargs,
返回一个 Jordan 块
- 参数:
- 大小整数,可选
指定Jordan块矩阵的形状。
- 特征值数字或符号
指定矩阵主对角线的值。
备注
关键字
eigenval也被指定为此关键字的别名,但不推荐使用。我们可能会在后续版本中弃用该别名。
- 乐队‘upper’ 或 ‘lower’, 可选
指定在非对角线上放置 \(1\) 的位置。
- cls矩阵,可选
指定输出表单的矩阵类。
如果没有指定,将返回执行该方法的类类型。
- 返回:
- 矩阵
一个约旦块矩阵。
- Raises:
- ValueError
如果矩阵大小指定的参数不足,或者没有给出特征值。
参考文献
示例
创建一个默认的 Jordan 块:
>>> from sympy import Matrix >>> from sympy.abc import x >>> Matrix.jordan_block(4, x) Matrix([ [x, 1, 0, 0], [0, x, 1, 0], [0, 0, x, 1], [0, 0, 0, x]])
创建一个替代的 Jordan 块矩阵,其中 \(1\) 位于次对角线下方:
>>> Matrix.jordan_block(4, x, band='lower') Matrix([ [x, 0, 0, 0], [1, x, 0, 0], [0, 1, x, 0], [0, 0, 1, x]])
使用关键字参数创建一个Jordan块
>>> Matrix.jordan_block(size=4, eigenvalue=x) Matrix([ [x, 1, 0, 0], [0, x, 1, 0], [0, 0, x, 1], [0, 0, 0, x]])
- jordan_form(
- calc_transform=True,
- **kwargs,
返回 \((P, J)\),其中 \(J\) 是一个约旦块矩阵,\(P\) 是一个矩阵,使得 \(M = P J P^{-1}\)
- 参数:
- calc_transform布尔
如果
False,则仅返回 \(J\)。- 砍布尔
在计算特征值和特征向量时,所有矩阵都会被转换为精确类型。因此,可能会出现近似误差。如果
chop==True,这些误差将被截断。
参见
示例
>>> from sympy import Matrix >>> M = Matrix([[ 6, 5, -2, -3], [-3, -1, 3, 3], [ 2, 1, -2, -3], [-1, 1, 5, 5]]) >>> P, J = M.jordan_form() >>> J Matrix([ [2, 1, 0, 0], [0, 2, 0, 0], [0, 0, 2, 1], [0, 0, 0, 2]])
- left_eigenvects(**flags)[源代码][源代码]¶
返回左特征向量和特征值。
此函数返回左特征向量的三元组列表(特征值,重数,基)。选项与 eigenvects() 相同,即
**flags参数直接传递给 eigenvects()。示例
>>> from sympy import Matrix >>> M = Matrix([[0, 1, 1], [1, 0, 0], [1, 1, 1]]) >>> M.eigenvects() [(-1, 1, [Matrix([ [-1], [ 1], [ 0]])]), (0, 1, [Matrix([ [ 0], [-1], [ 1]])]), (2, 1, [Matrix([ [2/3], [1/3], [ 1]])])] >>> M.left_eigenvects() [(-1, 1, [Matrix([[-2, 1, 1]])]), (0, 1, [Matrix([[-1, -1, 1]])]), (2, 1, [Matrix([[1, 1, 1]])])]
- limit(*args)[源代码][源代码]¶
计算矩阵中每个元素的极限。
args将被传递给limit函数。示例
>>> from sympy import Matrix >>> from sympy.abc import x, y >>> M = Matrix([[x, y], [1, 0]]) >>> M.limit(x, 2) Matrix([ [2, y], [1, 0]])
- log(simplify=<function cancel>)[源代码][源代码]¶
返回一个方阵的对数。
- 参数:
- 简化函数, 布尔值
用于简化结果的函数。
默认是
cancel,这对于减少符号矩阵的取倒数和逆运算的表达式增长是有效的。
示例
>>> from sympy import S, Matrix
正定矩阵的例子:
>>> m = Matrix([[1, 1], [0, 1]]) >>> m.log() Matrix([ [0, 1], [0, 0]])
>>> m = Matrix([[S(5)/4, S(3)/4], [S(3)/4, S(5)/4]]) >>> m.log() Matrix([ [ 0, log(2)], [log(2), 0]])
非正定矩阵的例子:
>>> m = Matrix([[S(3)/4, S(5)/4], [S(5)/4, S(3)/4]]) >>> m.log() Matrix([ [ I*pi/2, log(2) - I*pi/2], [log(2) - I*pi/2, I*pi/2]])
>>> m = Matrix( ... [[0, 0, 0, 1], ... [0, 0, 1, 0], ... [0, 1, 0, 0], ... [1, 0, 0, 0]]) >>> m.log() Matrix([ [ I*pi/2, 0, 0, -I*pi/2], [ 0, I*pi/2, -I*pi/2, 0], [ 0, -I*pi/2, I*pi/2, 0], [-I*pi/2, 0, 0, I*pi/2]])
- lower_triangular(k=0)[源代码][源代码]¶
返回矩阵中第 k 个对角线及其以下的元素。如果未指定 k,则仅返回矩阵的下三角部分。
示例
>>> from sympy import ones >>> A = ones(4) >>> A.lower_triangular() Matrix([ [1, 0, 0, 0], [1, 1, 0, 0], [1, 1, 1, 0], [1, 1, 1, 1]])
>>> A.lower_triangular(-2) Matrix([ [0, 0, 0, 0], [0, 0, 0, 0], [1, 0, 0, 0], [1, 1, 0, 0]])
>>> A.lower_triangular(1) Matrix([ [1, 1, 0, 0], [1, 1, 1, 0], [1, 1, 1, 1], [1, 1, 1, 1]])
- minor(i, j, method='berkowitz')[源代码][源代码]¶
返回
M的 (i,j) 子式。也就是说,返回通过从M中删除第 \(i\) 行和第 \(j\) 列得到的矩阵的行列式。- 参数:
- i, j整数
要排除的行和列以获得子矩阵。
- 方法字符串,可选
用于查找子矩阵行列式的方法,可以是 “bareiss”、”berkowitz”、”bird”、”laplace” 或 “lu”。
示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> M.minor(1, 1) -12
- minor_submatrix(i, j)[源代码][源代码]¶
返回通过从
M中移除第 \(i\) 行和第 \(j\) 列得到的子矩阵(适用于Python风格的负索引)。- 参数:
- i, j整数
要排除的行和列以获得子矩阵。
示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> M.minor_submatrix(1, 1) Matrix([ [1, 3], [7, 9]])
- multiply(other, dotprodsimp=None)[源代码][源代码]¶
与 __mul__() 相同,但带有可选的简化。
- 参数:
- dotprodsimpbool, 可选
指定在矩阵乘法期间是否使用中间项代数简化来控制表达式膨胀,从而加快计算速度。默认是关闭的。
- multiply_elementwise(other)[源代码][源代码]¶
返回 A 和 B 的哈达玛积(逐元素乘积)
示例
>>> from sympy import Matrix >>> A = Matrix([[0, 1, 2], [3, 4, 5]]) >>> B = Matrix([[1, 10, 100], [100, 10, 1]]) >>> A.multiply_elementwise(B) Matrix([ [ 0, 10, 200], [300, 40, 5]])
- norm(ord=None)[源代码][源代码]¶
返回矩阵或向量的范数。
在最简单的情况下,这是向量的几何尺寸。其他范数可以通过 ord 参数指定。
序数
矩阵的范数
向量的范数
无
Frobenius 范数
2-范数
‘fro’
Frobenius 范数
不存在
信息
最大行和
max(abs(x))
-inf
–
min(abs(x))
toctree是一个 reStructuredText 指令 ,这是一个非常多功能的标记。指令可以有参数、选项和内容。最大列和
如下
-1
–
如下
2
2-范数 (最大奇异值)
如下
-2
最小奇异值
如下
其他
不存在
sum(abs(x)**ord)**(1./ord)
参见
示例
>>> from sympy import Matrix, Symbol, trigsimp, cos, sin, oo >>> x = Symbol('x', real=True) >>> v = Matrix([cos(x), sin(x)]) >>> trigsimp( v.norm() ) 1 >>> v.norm(10) (sin(x)**10 + cos(x)**10)**(1/10) >>> A = Matrix([[1, 1], [1, 1]]) >>> A.norm(1) # maximum sum of absolute values of A is 2 2 >>> A.norm(2) # Spectral norm (max of |Ax|/|x| under 2-vector-norm) 2 >>> A.norm(-2) # Inverse spectral norm (smallest singular value) 0 >>> A.norm() # Frobenius Norm 2 >>> A.norm(oo) # Infinity Norm 2 >>> Matrix([1, -2]).norm(oo) 2 >>> Matrix([-1, 2]).norm(-oo) 1
- normalized(
- iszerofunc=<function _iszero>,
返回
self的规范化版本。- 参数:
- iszerofunc函数,可选
一个用于确定
self是否为零向量的函数。默认的_iszero测试每个元素是否精确为零。
- 返回:
- 矩阵
self的归一化向量形式。它的长度与单位向量相同。然而,对于范数为0的向量,将返回零向量。
- Raises:
- ShapeError
如果矩阵不是以向量形式存在。
参见
- nullspace(
- simplify=False,
- iszerofunc=<function _iszero>,
返回一个向量列表(矩阵对象),这些向量跨越
M的零空间示例
>>> from sympy import Matrix >>> M = Matrix(3, 3, [1, 3, 0, -2, -6, 0, 3, 9, 6]) >>> M Matrix([ [ 1, 3, 0], [-2, -6, 0], [ 3, 9, 6]]) >>> M.nullspace() [Matrix([ [-3], [ 1], [ 0]])]
- classmethod ones(rows, cols=None, **kwargs)[源代码][源代码]¶
返回一个全为1的矩阵。
- 参数:
- 行矩阵的行
- cols矩阵的列(如果为 None,则 cols=rows)
- classmethod orthogonalize(*vecs, **kwargs)[源代码][源代码]¶
对
vecs中的向量应用格拉姆-施密特正交化过程。- 参数:
- vecs
要使其正交的向量
- 规范化布尔
如果
True,返回一个标准正交基。- rankcheck布尔
如果
True,在遇到线性相关向量时,计算不会停止。如果
False,当发现任何零向量或线性相关向量时,将引发ValueError。
- 返回:
- 列表
正交(或标准正交)基向量列表。
参考文献
示例
>>> from sympy import I, Matrix >>> v = [Matrix([1, I]), Matrix([1, -I])] >>> Matrix.orthogonalize(*v) [Matrix([ [1], [I]]), Matrix([ [ 1], [-I]])]
- per()[源代码][源代码]¶
返回矩阵的永久值。与行列式不同,永久值对正方形和非正方形矩阵都有定义。
对于一个 m x n 矩阵,其中 m 小于或等于 n,其定义为对大小小于或等于 m 的排列 s 在 [1, 2, … n] 上的和,乘积从 i = 1 到 m 的 M[i, s[i]]。取转置不会影响永久值。
对于方阵,这与行列式的排列定义相同,但它不考虑排列的符号。使用此定义计算永久性效率相当低,因此这里使用Ryser公式。
参考文献
[1]Frank Ben 教授的笔记: https://math.berkeley.edu/~bernd/ban275.pdf
[2]维基百科关于永久性的文章:https://en.wikipedia.org/wiki/Permanent_%28mathematics%29
[4]矩形矩阵的永久性 : https://arxiv.org/pdf/0904.3251.pdf
示例
>>> from sympy import Matrix >>> M = Matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> M.per() 450 >>> M = Matrix([1, 5, 7]) >>> M.per() 13
- permute(
- perm,
- orientation='rows',
- direction='forward',
通过给定的交换列表置换矩阵的行或列。
- 参数:
- 权限排列,列表,或列表的列表
排列的表示法。
如果是
Permutation,它会根据矩阵大小直接使用并进行一些调整。如果指定为列表的列表(例如,
[[0, 1], [0, 2]]),则置换是通过应用循环乘积形成的。循环乘积的应用方向如下所述。如果指定为列表,该列表应表示置换的数组形式。(例如,
[1, 2, 0])这将形成交换函数 \(0 \mapsto 1, 1 \mapsto 2, 2\mapsto 0\)。- 方向‘行’, ‘列’
一个控制是否置换行或列的标志
- 方向‘forward’, ‘backward’
一个标志,用于控制是先应用列表开头的排列,还是先应用列表末尾的排列。
例如,如果排列规范是
[[0, 1], [0, 2]],如果标志设置为
'forward',循环将形成为 \(0 \mapsto 2, 2 \mapsto 1, 1 \mapsto 0\)。如果标志设置为
'backward',循环将形成为 \(0 \mapsto 1, 1 \mapsto 2, 2 \mapsto 0\)。如果参数
perm不是以列表的列表形式出现,此标志将无效。
注释
如果一个双射函数 \(\sigma : \mathbb{N}_0 \rightarrow \mathbb{N}_0\) 表示排列。
如果矩阵 \(A\) 是要置换的矩阵,表示为向量的水平或垂直堆叠:
\[\begin{split}A = \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{bmatrix} = \begin{bmatrix} \alpha_0 & \alpha_1 & \cdots & \alpha_{n-1} \end{bmatrix}\end{split}\]如果矩阵 \(B\) 是结果,矩阵行的排列定义为:
\[\begin{split}B := \begin{bmatrix} a_{\sigma(0)} \\ a_{\sigma(1)} \\ \vdots \\ a_{\sigma(n-1)} \end{bmatrix}\end{split}\]矩阵列的排列定义为:
\[B := \begin{bmatrix} \alpha_{\sigma(0)} & \alpha_{\sigma(1)} & \cdots & \alpha_{\sigma(n-1)} \end{bmatrix}\]示例
>>> from sympy import eye >>> M = eye(3) >>> M.permute([[0, 1], [0, 2]], orientation='rows', direction='forward') Matrix([ [0, 0, 1], [1, 0, 0], [0, 1, 0]])
>>> from sympy import eye >>> M = eye(3) >>> M.permute([[0, 1], [0, 2]], orientation='rows', direction='backward') Matrix([ [0, 1, 0], [0, 0, 1], [1, 0, 0]])
- permute_cols(
- swaps,
- direction='forward',
self.permute(swaps, orientation='cols', direction=direction)的别名参见
- permute_rows(
- swaps,
- direction='forward',
self.permute(swaps, orientation='rows', direction=direction)的别名参见
- pinv(method='RD')[源代码][源代码]¶
计算矩阵的 Moore-Penrose 伪逆。
对于任何矩阵,Moore-Penrose 伪逆存在且唯一。如果矩阵是可逆的,伪逆与逆相同。
- 参数:
- 方法字符串,可选
指定计算伪逆的方法。
如果
'RD',将使用秩分解。如果
'ED',将使用对角化方法。
参见
参考文献
[1]https://en.wikipedia.org/wiki/Moore-Penrose_伪逆
示例
通过秩分解计算伪逆 :
>>> from sympy import Matrix >>> A = Matrix([[1, 2, 3], [4, 5, 6]]) >>> A.pinv() Matrix([ [-17/18, 4/9], [ -1/9, 1/9], [ 13/18, -2/9]])
通过对角化计算伪逆 :
>>> B = A.pinv(method='ED') >>> B.simplify() >>> B Matrix([ [-17/18, 4/9], [ -1/9, 1/9], [ 13/18, -2/9]])
- pinv_solve(B, arbitrary_matrix=None)[源代码][源代码]¶
使用 Moore-Penrose 伪逆求解
Ax = B。可能存在零个、一个或无限个解。如果存在一个解,它将被返回。如果存在无限个解,将根据 arbitrary_matrix 的值返回一个解。如果不存在解,则返回最小二乘解。
- 参数:
- B矩阵
要解的方程的右侧。必须与矩阵A有相同的行数。
- 任意矩阵矩阵
如果系统是欠定的(例如,A 的列数多于行数),则可能存在无限多的解,具体取决于一个任意矩阵。此参数可以设置为一个特定的矩阵以供使用;如果是这样,它必须与 x 形状相同,具有与矩阵 A 列数相同的行数,以及与矩阵 B 相同的列数。如果保留为 None,则将使用一个包含形式为
wn_m的虚拟符号的适当矩阵,其中 n 和 m 分别是每个符号的行和列位置。
- 返回:
- x矩阵
满足
Ax = B的矩阵。将具有与矩阵 A 的列数相同的行数,以及与矩阵 B 相同的列数。
参见
注释
这可能会返回精确解或最小二乘解。要确定是哪一种,检查
A * A.pinv() * B == B。如果存在精确解,则为 True,如果仅存在最小二乘解,则为 False。请注意,该等式的左侧可能需要简化以正确比较右侧。参考文献
示例
>>> from sympy import Matrix >>> A = Matrix([[1, 2, 3], [4, 5, 6]]) >>> B = Matrix([7, 8]) >>> A.pinv_solve(B) Matrix([ [ _w0_0/6 - _w1_0/3 + _w2_0/6 - 55/18], [-_w0_0/3 + 2*_w1_0/3 - _w2_0/3 + 1/9], [ _w0_0/6 - _w1_0/3 + _w2_0/6 + 59/18]]) >>> A.pinv_solve(B, arbitrary_matrix=Matrix([0, 0, 0])) Matrix([ [-55/18], [ 1/9], [ 59/18]])
- pow(exp, method=None)[源代码][源代码]¶
返回 self**exp,其中 exp 是一个标量或符号。
- 参数:
- 方法multiply, mulsimp, jordan, cayley
如果选择 ‘multiply’,则使用递归进行指数运算。如果选择 ‘jordan’,则使用 Jordan 形式进行指数运算。如果选择 ‘cayley’,则使用 Cayley-Hamilton 定理进行指数运算。如果选择 ‘mulsimp’,则使用递归进行指数运算,并结合 dotprodsimp。这指定了在朴素矩阵幂运算期间是否使用中间项代数简化来控制表达式膨胀,从而加快计算速度。如果为 None,则它会启发式地决定使用哪种方法。
- print_nonzero(symb='X')[源代码][源代码]¶
显示非零条目的位置,以便快速查找形状。
示例
>>> from sympy import Matrix, eye >>> m = Matrix(2, 3, lambda i, j: i*3+j) >>> m Matrix([ [0, 1, 2], [3, 4, 5]]) >>> m.print_nonzero() [ XX] [XXX] >>> m = eye(4) >>> m.print_nonzero("x") [x ] [ x ] [ x ] [ x]
- project(v)[源代码][源代码]¶
返回
self在包含v的直线上的投影。示例
>>> from sympy import Matrix, S, sqrt >>> V = Matrix([sqrt(3)/2, S.Half]) >>> x = Matrix([[1, 0]]) >>> V.project(x) Matrix([[sqrt(3)/2, 0]]) >>> V.project(-x) Matrix([[sqrt(3)/2, 0]])
- rank(
- iszerofunc=<function _iszero>,
- simplify=False,
返回矩阵的秩。
示例
>>> from sympy import Matrix >>> from sympy.abc import x >>> m = Matrix([[1, 2], [x, 1 - 1/x]]) >>> m.rank() 2 >>> n = Matrix(3, 3, range(1, 10)) >>> n.rank() 2
- rank_decomposition(
- iszerofunc=<function _iszero>,
- simplify=False,
返回一对矩阵 (\(C\), \(F\)),它们的秩相匹配,使得 \(A = C F\)。
- 参数:
- iszerofunc函数,可选
用于检测一个元素是否可以作为支点的函数。默认使用
lambda x: x.is_zero。- 简化布尔值或函数,可选
一个用于在寻找枢轴时简化元素的函数。默认情况下使用SymPy的``simplify``。
- 返回:
- (摄氏度, 华氏度)矩阵
\(C\) 和 \(F\) 是与 \(A\) 具有相同秩的满秩矩阵,它们的乘积给出 \(A\)。
参见注释以获取更多数学细节。
注释
获得 \(F\),即 \(A\) 的简化行阶梯形式(RREF),等同于创建一个乘积
\[E_n E_{n-1} ... E_1 A = F\]其中 \(E_n, E_{n-1}, \dots, E_1\) 是对应于每一行简化步骤的消去矩阵或置换矩阵。
消除矩阵的相同乘积的逆给出 \(C\):
\[C = \left(E_n E_{n-1} \dots E_1\right)^{-1}\]然而,实际上并不需要计算逆矩阵:矩阵 \(C\) 的列是原始矩阵中与 \(F\) 的主元列具有相同列索引的列。
参考文献
[1][2]Piziak, R.; Odell, P. L. (1999年6月1日). “矩阵的满秩分解”. 数学杂志. 72 (3): 193. doi:10.2307/2690882
示例
>>> from sympy import Matrix >>> A = Matrix([ ... [1, 3, 1, 4], ... [2, 7, 3, 9], ... [1, 5, 3, 1], ... [1, 2, 0, 8] ... ]) >>> C, F = A.rank_decomposition() >>> C Matrix([ [1, 3, 4], [2, 7, 9], [1, 5, 1], [1, 2, 8]]) >>> F Matrix([ [1, 0, -2, 0], [0, 1, 1, 0], [0, 0, 0, 1]]) >>> C * F == A True
- refine(assumptions=True)[源代码][源代码]¶
对矩阵的每个元素应用细化。
示例
>>> from sympy import Symbol, Matrix, Abs, sqrt, Q >>> x = Symbol('x') >>> Matrix([[Abs(x)**2, sqrt(x**2)],[sqrt(x**2), Abs(x)**2]]) Matrix([ [ Abs(x)**2, sqrt(x**2)], [sqrt(x**2), Abs(x)**2]]) >>> _.refine(Q.real(x)) Matrix([ [ x**2, Abs(x)], [Abs(x), x**2]])
- replace(
- F,
- G,
- map=False,
- simultaneous=True,
- exact=None,
将矩阵条目中的函数 F 替换为函数 G。
示例
>>> from sympy import symbols, Function, Matrix >>> F, G = symbols('F, G', cls=Function) >>> M = Matrix(2, 2, lambda i, j: F(i+j)) ; M Matrix([ [F(0), F(1)], [F(1), F(2)]]) >>> N = M.replace(F,G) >>> N Matrix([ [G(0), G(1)], [G(1), G(2)]])
- reshape(rows, cols)[源代码][源代码]¶
重塑矩阵。元素总数必须保持不变。
示例
>>> from sympy import Matrix >>> m = Matrix(2, 3, lambda i, j: 1) >>> m Matrix([ [1, 1, 1], [1, 1, 1]]) >>> m.reshape(1, 6) Matrix([[1, 1, 1, 1, 1, 1]]) >>> m.reshape(3, 2) Matrix([ [1, 1], [1, 1], [1, 1]])
- rmultiply(other, dotprodsimp=None)[源代码][源代码]¶
与 __rmul__() 相同,但带有可选的简化功能。
- 参数:
- dotprodsimpbool, 可选
指定在矩阵乘法期间是否使用中间项代数简化来控制表达式膨胀,从而加快计算速度。默认是关闭的。
- rot90(k=1)[源代码][源代码]¶
将矩阵旋转90度
- 参数:
- k整数
指定矩阵旋转90度的次数(正数时顺时针,负数时逆时针)。
示例
>>> from sympy import Matrix, symbols >>> A = Matrix(2, 2, symbols('a:d')) >>> A Matrix([ [a, b], [c, d]])
将矩阵顺时针旋转一次:
>>> A.rot90(1) Matrix([ [c, a], [d, b]])
将矩阵逆时针旋转两次:
>>> A.rot90(-2) Matrix([ [d, c], [b, a]])
- row_insert(pos, other)[源代码][源代码]¶
在给定的行位置插入一行或多行。
参见
示例
>>> from sympy import zeros, ones >>> M = zeros(3) >>> V = ones(1, 3) >>> M.row_insert(1, V) Matrix([ [0, 0, 0], [1, 1, 1], [0, 0, 0], [0, 0, 0]])
- row_join(other)[源代码][源代码]¶
将两个矩阵沿着自身的最后一列和rhs的第一列进行连接
示例
>>> from sympy import zeros, ones >>> M = zeros(3) >>> V = ones(3, 1) >>> M.row_join(V) Matrix([ [0, 0, 0, 1], [0, 0, 0, 1], [0, 0, 0, 1]])
- rowspace(simplify=False)[源代码][源代码]¶
返回一个向量列表,这些向量跨越矩阵
M的行空间。示例
>>> from sympy import Matrix >>> M = Matrix(3, 3, [1, 3, 0, -2, -6, 0, 3, 9, 6]) >>> M Matrix([ [ 1, 3, 0], [-2, -6, 0], [ 3, 9, 6]]) >>> M.rowspace() [Matrix([[1, 3, 0]]), Matrix([[0, 0, 6]])]
- rref(
- iszerofunc=<function _iszero>,
- simplify=False,
- pivots=True,
- normalize_last=True,
返回矩阵的简化行阶梯形式和主元变量的索引。
- 参数:
- iszerofunc函数
用于检测一个元素是否可以作为支点的函数。默认使用
lambda x: x.is_zero。- 简化函数
一个用于在寻找枢轴时简化元素的函数。默认情况下使用SymPy的``simplify``。
- 支点真或假
如果
True,则返回一个包含行简化矩阵和枢轴列元组的元组。如果False,则仅返回行简化矩阵。- normalize_last真或假
如果
True,在所有位于每个枢轴上下的条目都被清零之前,不会将枢轴归一化为 \(1\)。这意味着行约简算法在最后一步之前是无分数的。如果False,则使用朴素的行约简过程,其中每个枢轴在用于清零枢轴上下的行操作之前被归一化为 \(1\)。
注释
normalize_last=True的默认值可以显著加快行简化速度,特别是在包含符号的矩阵上。然而,如果你依赖于行简化算法留下的矩阵条目的形式,请设置normalize_last=False示例
>>> from sympy import Matrix >>> from sympy.abc import x >>> m = Matrix([[1, 2], [x, 1 - 1/x]]) >>> m.rref() (Matrix([ [1, 0], [0, 1]]), (0, 1)) >>> rref_matrix, rref_pivots = m.rref() >>> rref_matrix Matrix([ [1, 0], [0, 1]]) >>> rref_pivots (0, 1)
iszerofunc可以修正矩阵中浮点值的舍入误差。在以下示例中,调用rref()会导致浮点误差,错误地行简化矩阵。iszerofunc= lambda x: abs(x) < 1e-9将足够小的数字设置为零,从而避免此错误。>>> m = Matrix([[0.9, -0.1, -0.2, 0], [-0.8, 0.9, -0.4, 0], [-0.1, -0.8, 0.6, 0]]) >>> m.rref() (Matrix([ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]]), (0, 1, 2)) >>> m.rref(iszerofunc=lambda x:abs(x)<1e-9) (Matrix([ [1, 0, -0.301369863013699, 0], [0, 1, -0.712328767123288, 0], [0, 0, 0, 0]]), (0, 1))
- rref_rhs(rhs)[源代码][源代码]¶
返回矩阵的简化行阶梯形式,以及在简化步骤后显示右侧的矩阵。
rhs必须与self具有相同的行数。示例
>>> from sympy import Matrix, symbols >>> r1, r2 = symbols('r1 r2') >>> Matrix([[1, 1], [2, 1]]).rref_rhs(Matrix([r1, r2])) (Matrix([ [1, 0], [0, 1]]), Matrix([ [ -r1 + r2], [2*r1 - r2]]))
- property shape¶
矩阵的形状(维度)作为 2 元组 (行数, 列数)。
示例
>>> from sympy import zeros >>> M = zeros(2, 3) >>> M.shape (2, 3) >>> M.rows 2 >>> M.cols 3
- simplify(**kwargs)[源代码][源代码]¶
对矩阵的每个元素应用简化。
示例
>>> from sympy.abc import x, y >>> from sympy import SparseMatrix, sin, cos >>> SparseMatrix(1, 1, [x*sin(y)**2 + x*cos(y)**2]) Matrix([[x*sin(y)**2 + x*cos(y)**2]]) >>> _.simplify() Matrix([[x]])
- singular_value_decomposition()[源代码][源代码]¶
返回一个压缩的奇异值分解。
示例
我们首先取一个满秩矩阵:
>>> from sympy import Matrix >>> A = Matrix([[1, 2],[2,1]]) >>> U, S, V = A.singular_value_decomposition() >>> U Matrix([ [ sqrt(2)/2, sqrt(2)/2], [-sqrt(2)/2, sqrt(2)/2]]) >>> S Matrix([ [1, 0], [0, 3]]) >>> V Matrix([ [-sqrt(2)/2, sqrt(2)/2], [ sqrt(2)/2, sqrt(2)/2]])
如果一个矩阵是方阵且满秩,那么 U 和 V 在两个方向上都是正交的。
>>> U * U.H Matrix([ [1, 0], [0, 1]]) >>> U.H * U Matrix([ [1, 0], [0, 1]])
>>> V * V.H Matrix([ [1, 0], [0, 1]]) >>> V.H * V Matrix([ [1, 0], [0, 1]]) >>> A == U * S * V.H True
>>> C = Matrix([ ... [1, 0, 0, 0, 2], ... [0, 0, 3, 0, 0], ... [0, 0, 0, 0, 0], ... [0, 2, 0, 0, 0], ... ]) >>> U, S, V = C.singular_value_decomposition()
>>> V.H * V Matrix([ [1, 0, 0], [0, 1, 0], [0, 0, 1]]) >>> V * V.H Matrix([ [1/5, 0, 0, 0, 2/5], [ 0, 1, 0, 0, 0], [ 0, 0, 1, 0, 0], [ 0, 0, 0, 0, 0], [2/5, 0, 0, 0, 4/5]])
如果你想将结果扩展为完整的正交分解,你应该用另一个正交列来扩展 \(V\)。
你可以将任意一组线性无关的标准基附加到其他每一列,然后你可以运行Gram-Schmidt过程使它们扩展为正交基。
>>> V_aug = V.row_join(Matrix([[0,0,0,0,1], ... [0,0,0,1,0]]).H) >>> V_aug = V_aug.QRdecomposition()[0] >>> V_aug Matrix([ [0, sqrt(5)/5, 0, -2*sqrt(5)/5, 0], [1, 0, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 0, 1], [0, 2*sqrt(5)/5, 0, sqrt(5)/5, 0]]) >>> V_aug.H * V_aug Matrix([ [1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]) >>> V_aug * V_aug.H Matrix([ [1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]])
同样地,我们增强 U
>>> U_aug = U.row_join(Matrix([0,0,1,0])) >>> U_aug = U_aug.QRdecomposition()[0] >>> U_aug Matrix([ [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1], [1, 0, 0, 0]])
>>> U_aug.H * U_aug Matrix([ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]) >>> U_aug * U_aug.H Matrix([ [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])
我们在S中添加2个零列和一行
>>> S_aug = S.col_join(Matrix([[0,0,0]])) >>> S_aug = S_aug.row_join(Matrix([[0,0,0,0], ... [0,0,0,0]]).H) >>> S_aug Matrix([ [2, 0, 0, 0, 0], [0, sqrt(5), 0, 0, 0], [0, 0, 3, 0, 0], [0, 0, 0, 0, 0]])
>>> U_aug * S_aug * V_aug.H == C True
- singular_values()[源代码][源代码]¶
计算矩阵的奇异值
示例
>>> from sympy import Matrix, Symbol >>> x = Symbol('x', real=True) >>> M = Matrix([[0, 1, 0], [0, x, 0], [-1, 0, 0]]) >>> M.singular_values() [sqrt(x**2 + 1), 1, 0]
- solve(rhs, method='GJ')[源代码][源代码]¶
求解存在唯一解的线性方程。
- 参数:
- rhs矩阵
表示线性方程右侧的向量。
- 方法字符串,可选
如果设置为
'GJ'或'GE',将使用高斯-若尔当消元法,该方法在gauss_jordan_solve例程中实现。如果设置为
'LU',将使用LUsolve例程。如果设置为
'QR',将使用QRsolve例程。如果设置为
'PINV',将使用pinv_solve例程。如果设置为
'CRAMER',将使用cramer_solve例程。它还支持适用于特殊线性系统的方法
对于正定系统:
如果设置为
'CH',将使用cholesky_solve例程。如果设置为
'LDL',将使用LDLsolve例程。要使用不同的方法并通过逆运算来计算解,请使用在 .inv() 文档字符串中定义的方法。
- 返回:
- 解决方案矩阵
表示解决方案的向量。
- Raises:
- ValueError
如果没有唯一的解决方案,则会引发
ValueError。如果
M不是方阵,将会抛出ValueError并建议使用不同的例程来求解系统。
- solve_least_squares(rhs, method='CH')[源代码][源代码]¶
返回对数据的最小二乘拟合。
- 参数:
- rhs矩阵
表示线性方程右侧的向量。
- 方法字符串或布尔值,可选
如果设置为
'CH',将使用cholesky_solve例程。如果设置为
'LDL',将使用LDLsolve例程。如果设置为
'QR',将使用QRsolve例程。如果设置为
'PINV',将使用pinv_solve例程。否则,将使用
M的共轭来创建一个方程组,该方程组与由method定义的提示一起传递给solve。
- 返回:
- 解决方案矩阵
表示解决方案的向量。
示例
>>> from sympy import Matrix, ones >>> A = Matrix([1, 2, 3]) >>> B = Matrix([2, 3, 4]) >>> S = Matrix(A.row_join(B)) >>> S Matrix([ [1, 2], [2, 3], [3, 4]])
如果 S 的每一行代表 Ax + By 的系数,且 x 和 y 是 [2, 3],那么 S*xy 是:
>>> r = S*Matrix([2, 3]); r Matrix([ [ 8], [13], [18]])
但是让我们将中间值加1,然后求解xy的最小二乘值:
>>> xy = S.solve_least_squares(Matrix([8, 14, 18])); xy Matrix([ [ 5/3], [10/3]])
错误由 S*xy - r 给出:
>>> S*xy - r Matrix([ [1/3], [1/3], [1/3]]) >>> _.norm().n(2) 0.58
如果使用不同的 xy,范数将会更高:
>>> xy += ones(2, 1)/10 >>> (S*xy - r).norm().n(2) 1.5
- strongly_connected_components()[源代码][源代码]¶
当一个方阵被视为加权图时,返回图中强连通顶点的列表。
示例
>>> from sympy import Matrix >>> A = Matrix([ ... [44, 0, 0, 0, 43, 0, 45, 0, 0], ... [0, 66, 62, 61, 0, 68, 0, 60, 67], ... [0, 0, 22, 21, 0, 0, 0, 20, 0], ... [0, 0, 12, 11, 0, 0, 0, 10, 0], ... [34, 0, 0, 0, 33, 0, 35, 0, 0], ... [0, 86, 82, 81, 0, 88, 0, 80, 87], ... [54, 0, 0, 0, 53, 0, 55, 0, 0], ... [0, 0, 2, 1, 0, 0, 0, 0, 0], ... [0, 76, 72, 71, 0, 78, 0, 70, 77]]) >>> A.strongly_connected_components() [[0, 4, 6], [2, 3, 7], [1, 5, 8]]
- strongly_connected_components_decomposition(
- lower=True,
仅使用排列将一个方阵分解为块三角形式。
- 参数:
- 下限布尔
当
True时,使 \(B\) 为下块三角形。否则,使 \(B\) 为上块三角形。
- 返回:
- P, B排列矩阵, 块矩阵
P 是相似变换中的置换矩阵,如解释中所述。而 B 是置换结果的分块三角矩阵。
示例
>>> from sympy import Matrix, pprint >>> A = Matrix([ ... [44, 0, 0, 0, 43, 0, 45, 0, 0], ... [0, 66, 62, 61, 0, 68, 0, 60, 67], ... [0, 0, 22, 21, 0, 0, 0, 20, 0], ... [0, 0, 12, 11, 0, 0, 0, 10, 0], ... [34, 0, 0, 0, 33, 0, 35, 0, 0], ... [0, 86, 82, 81, 0, 88, 0, 80, 87], ... [54, 0, 0, 0, 53, 0, 55, 0, 0], ... [0, 0, 2, 1, 0, 0, 0, 0, 0], ... [0, 76, 72, 71, 0, 78, 0, 70, 77]])
一个下块三角分解:
>>> P, B = A.strongly_connected_components_decomposition() >>> pprint(P) PermutationMatrix((8)(1 4 3 2 6)(5 7)) >>> pprint(B) [[44 43 45] [0 0 0] [0 0 0] ] [[ ] [ ] [ ] ] [[34 33 35] [0 0 0] [0 0 0] ] [[ ] [ ] [ ] ] [[54 53 55] [0 0 0] [0 0 0] ] [ ] [ [0 0 0] [22 21 20] [0 0 0] ] [ [ ] [ ] [ ] ] [ [0 0 0] [12 11 10] [0 0 0] ] [ [ ] [ ] [ ] ] [ [0 0 0] [2 1 0 ] [0 0 0] ] [ ] [ [0 0 0] [62 61 60] [66 68 67]] [ [ ] [ ] [ ]] [ [0 0 0] [82 81 80] [86 88 87]] [ [ ] [ ] [ ]] [ [0 0 0] [72 71 70] [76 78 77]]
>>> P = P.as_explicit() >>> B = B.as_explicit() >>> P.T * B * P == A True
上块三角分解:
>>> P, B = A.strongly_connected_components_decomposition(lower=False) >>> pprint(P) PermutationMatrix((0 1 5 7 4 3 2 8 6)) >>> pprint(B) [[66 68 67] [62 61 60] [0 0 0] ] [[ ] [ ] [ ] ] [[86 88 87] [82 81 80] [0 0 0] ] [[ ] [ ] [ ] ] [[76 78 77] [72 71 70] [0 0 0] ] [ ] [ [0 0 0] [22 21 20] [0 0 0] ] [ [ ] [ ] [ ] ] [ [0 0 0] [12 11 10] [0 0 0] ] [ [ ] [ ] [ ] ] [ [0 0 0] [2 1 0 ] [0 0 0] ] [ ] [ [0 0 0] [0 0 0] [44 43 45]] [ [ ] [ ] [ ]] [ [0 0 0] [0 0 0] [34 33 35]] [ [ ] [ ] [ ]] [ [0 0 0] [0 0 0] [54 53 55]]
>>> P = P.as_explicit() >>> B = B.as_explicit() >>> P.T * B * P == A True
- subs(*args, **kwargs)[源代码][源代码]¶
返回一个新的矩阵,其中每个条目都应用了 subs。
示例
>>> from sympy.abc import x, y >>> from sympy import SparseMatrix, Matrix >>> SparseMatrix(1, 1, [x]) Matrix([[x]]) >>> _.subs(x, y) Matrix([[y]]) >>> Matrix(_).subs(y, x) Matrix([[x]])
- table(
- printer,
- rowstart='[',
- rowend=']',
- rowsep='\n',
- colsep=', ',
- align='right',
以表格形式表示的矩阵字符串。
printer是用于元素的打印机(通常类似于 StrPrinter())rowstart是用于开始每一行的字符串(默认是’[’)。rowend是用于结束每一行的字符串(默认是 ‘]’)。rowsep是用于分隔行的字符串(默认是换行符)。colsep是用于分隔列的字符串(默认是 ‘, ‘)。align定义了元素的对齐方式。必须是 ‘left’、’right’ 或 ‘center’ 之一。你也可以分别使用 ‘<’、’>’ 和 ‘^’ 来表示相同的意思。这是用于矩阵的字符串打印机。
示例
>>> from sympy import Matrix, StrPrinter >>> M = Matrix([[1, 2], [-33, 4]]) >>> printer = StrPrinter() >>> M.table(printer) '[ 1, 2]\n[-33, 4]' >>> print(M.table(printer)) [ 1, 2] [-33, 4] >>> print(M.table(printer, rowsep=',\n')) [ 1, 2], [-33, 4] >>> print('[%s]' % M.table(printer, rowsep=',\n')) [[ 1, 2], [-33, 4]] >>> print(M.table(printer, colsep=' ')) [ 1 2] [-33 4] >>> print(M.table(printer, align='center')) [ 1 , 2] [-33, 4] >>> print(M.table(printer, rowstart='{', rowend='}')) { 1, 2} {-33, 4}
- todod()[源代码][源代码]¶
返回矩阵作为包含矩阵非零元素的字典的字典
示例
>>> from sympy import Matrix >>> A = Matrix([[0, 1],[0, 3]]) >>> A Matrix([ [0, 1], [0, 3]]) >>> A.todod() {0: {1: 1}, 1: {1: 3}}
- todok()[源代码][源代码]¶
返回矩阵作为键的字典。
示例
>>> from sympy import Matrix >>> M = Matrix.eye(3) >>> M.todok() {(0, 0): 1, (1, 1): 1, (2, 2): 1}
- tolist()[源代码][源代码]¶
返回矩阵作为嵌套的Python列表。
示例
>>> from sympy import Matrix, ones >>> m = Matrix(3, 3, range(9)) >>> m Matrix([ [0, 1, 2], [3, 4, 5], [6, 7, 8]]) >>> m.tolist() [[0, 1, 2], [3, 4, 5], [6, 7, 8]] >>> ones(3, 0).tolist() [[], [], []]
当没有行时,将无法判断原始矩阵中有多少列:
>>> ones(0, 3).tolist() []
- trace()[源代码][源代码]¶
返回一个方阵的迹,即对角元素之和。
示例
>>> from sympy import Matrix >>> A = Matrix(2, 2, [1, 2, 3, 4]) >>> A.trace() 5
- transpose()[源代码][源代码]¶
返回矩阵的转置。
参见
conjugate逐元素共轭
示例
>>> from sympy import Matrix >>> A = Matrix(2, 2, [1, 2, 3, 4]) >>> A.transpose() Matrix([ [1, 3], [2, 4]])
>>> from sympy import Matrix, I >>> m=Matrix(((1, 2+I), (3, 4))) >>> m Matrix([ [1, 2 + I], [3, 4]]) >>> m.transpose() Matrix([ [ 1, 3], [2 + I, 4]]) >>> m.T == m.transpose() True
- upper_hessenberg_decomposition()[源代码][源代码]¶
将一个矩阵转换为Hessenberg矩阵H。
返回两个矩阵 H, P 使得 \(P H P^{T} = A\),其中 H 是上 Hessenberg 矩阵,P 是正交矩阵。
参考文献
示例
>>> from sympy import Matrix >>> A = Matrix([ ... [1,2,3], ... [-3,5,6], ... [4,-8,9], ... ]) >>> H, P = A.upper_hessenberg_decomposition() >>> H Matrix([ [1, 6/5, 17/5], [5, 213/25, -134/25], [0, 216/25, 137/25]]) >>> P Matrix([ [1, 0, 0], [0, -3/5, 4/5], [0, 4/5, 3/5]]) >>> P * H * P.H == A True
- upper_triangular(k=0)[源代码][源代码]¶
返回矩阵中第 k 条对角线及其以上的元素。如果未指定 k,则仅返回矩阵的上三角部分。
示例
>>> from sympy import ones >>> A = ones(4) >>> A.upper_triangular() Matrix([ [1, 1, 1, 1], [0, 1, 1, 1], [0, 0, 1, 1], [0, 0, 0, 1]])
>>> A.upper_triangular(2) Matrix([ [0, 0, 1, 1], [0, 0, 0, 1], [0, 0, 0, 0], [0, 0, 0, 0]])
>>> A.upper_triangular(-1) Matrix([ [1, 1, 1, 1], [1, 1, 1, 1], [0, 1, 1, 1], [0, 0, 1, 1]])
- values()[源代码][源代码]¶
返回 self 的非零值。
示例
>>> from sympy import Matrix >>> m = Matrix([[0, 1], [2, 3]]) >>> m.values() [1, 2, 3]
- vec()[源代码][源代码]¶
通过堆叠列将矩阵转换为一列矩阵
参见
示例
>>> from sympy import Matrix >>> m=Matrix([[1, 3], [2, 4]]) >>> m Matrix([ [1, 3], [2, 4]]) >>> m.vec() Matrix([ [1], [2], [3], [4]])
- vech(
- diagonal=True,
- check_symmetry=True,
通过堆叠下三角中的元素,将矩阵重塑为列向量。
- 参数:
- 对角线bool, 可选
如果
True,它将包含对角线元素。- 检查对称性bool, 可选
如果
True,它会检查矩阵是否对称。
参见
注释
这应该适用于对称矩阵,而
vech可以用比vec更小的尺寸以向量形式表示对称矩阵。示例
>>> from sympy import Matrix >>> m=Matrix([[1, 2], [2, 3]]) >>> m Matrix([ [1, 2], [2, 3]]) >>> m.vech() Matrix([ [1], [2], [3]]) >>> m.vech(diagonal=False) Matrix([[2]])
- vee()[源代码][源代码]¶
从表示叉积的反对称矩阵返回一个3x1向量,使得
self * b等价于self.vee().cross(b)。示例
调用
vee会从反对称矩阵创建一个向量:>>> from sympy import Matrix >>> A = Matrix([[0, -3, 2], [3, 0, -1], [-2, 1, 0]]) >>> a = A.vee() >>> a Matrix([ [1], [2], [3]])
计算原始矩阵与向量的矩阵乘积相当于一个叉积:
>>> b = Matrix([3, 2, 1]) >>> A * b Matrix([ [-4], [ 8], [-4]])
>>> a.cross(b) Matrix([ [-4], [ 8], [-4]])
vee也可以用来检索角速度表达式。定义一个旋转矩阵:>>> from sympy import rot_ccw_axis3, trigsimp >>> from sympy.physics.mechanics import dynamicsymbols >>> theta = dynamicsymbols('theta') >>> R = rot_ccw_axis3(theta) >>> R Matrix([ [cos(theta(t)), -sin(theta(t)), 0], [sin(theta(t)), cos(theta(t)), 0], [ 0, 0, 1]])
我们可以检索角速度:
>>> Omega = R.T * R.diff() >>> Omega = trigsimp(Omega) >>> Omega.vee() Matrix([ [ 0], [ 0], [Derivative(theta(t), t)]])
- classmethod vstack(*args)[源代码][源代码]¶
返回一个矩阵,该矩阵是通过垂直连接参数(即通过重复应用 col_join)形成的。
示例
>>> from sympy import Matrix, eye >>> Matrix.vstack(eye(2), 2*eye(2)) Matrix([ [1, 0], [0, 1], [2, 0], [0, 2]])
- classmethod wilkinson(n, **kwargs)[源代码][源代码]¶
返回两个大小为 2*n + 1 的平方 Wilkinson 矩阵 \(W_{2n + 1}^-, W_{2n + 1}^+ =\) Wilkinson(n)
参考文献
[2]Wilkinson, 《代数特征值问题》, Claredon Press, 牛津, 1965, 662页。
示例
>>> from sympy import Matrix >>> wminus, wplus = Matrix.wilkinson(3) >>> wminus Matrix([ [-3, 1, 0, 0, 0, 0, 0], [ 1, -2, 1, 0, 0, 0, 0], [ 0, 1, -1, 1, 0, 0, 0], [ 0, 0, 1, 0, 1, 0, 0], [ 0, 0, 0, 1, 1, 1, 0], [ 0, 0, 0, 0, 1, 2, 1], [ 0, 0, 0, 0, 0, 1, 3]]) >>> wplus Matrix([ [3, 1, 0, 0, 0, 0, 0], [1, 2, 1, 0, 0, 0, 0], [0, 1, 1, 1, 0, 0, 0], [0, 0, 1, 0, 1, 0, 0], [0, 0, 0, 1, 1, 1, 0], [0, 0, 0, 0, 1, 2, 1], [0, 0, 0, 0, 0, 1, 3]])
矩阵异常¶
- class sympy.matrices.matrixbase.MatrixError[源代码][源代码]¶
- 属性:
- 参数
方法
with_tracebackException.with_traceback(tb) -- 将 self.__traceback__ 设置为 tb 并返回 self。
矩阵函数¶
- sympy.matrices.dense.matrix_multiply_elementwise(A, B)[源代码][源代码]¶
返回 A 和 B 的哈达玛积(逐元素乘积)
>>> from sympy import Matrix, matrix_multiply_elementwise >>> A = Matrix([[0, 1, 2], [3, 4, 5]]) >>> B = Matrix([[1, 10, 100], [100, 10, 1]]) >>> matrix_multiply_elementwise(A, B) Matrix([ [ 0, 10, 200], [300, 40, 5]])
- sympy.matrices.dense.zeros(*args, **kwargs)[源代码][源代码]¶
返回一个由零组成的矩阵,具有
rows行和cols列;如果省略cols,将返回一个方阵。
- sympy.matrices.dense.ones(*args, **kwargs)[源代码][源代码]¶
返回一个由
rows行和cols列组成的单位矩阵;如果省略cols,则将返回一个方阵。
- sympy.matrices.dense.diag(*values, strict=True, unpack=False, **kwargs)[源代码][源代码]¶
返回一个将对角线上的值放置在提供的矩阵中。如果包含非方阵,它们将生成一个分块对角矩阵。
参见
示例
这个版本的 diag 是对 Matrix.diag 的一个薄包装,不同的是它将所有列表视为矩阵——即使给定的是单个列表。如果这不是你想要的,可以在列表前加上 \(*\) 或在设置中将 \(unpack\) 设为 \(True\)。
>>> from sympy import diag
>>> diag([1, 2, 3], unpack=True) # = diag(1,2,3) or diag(*[1,2,3]) Matrix([ [1, 0, 0], [0, 2, 0], [0, 0, 3]])
>>> diag([1, 2, 3]) # a column vector Matrix([ [1], [2], [3]])
- sympy.matrices.dense.jordan_cell(eigenval, n)[源代码][源代码]¶
创建一个 Jordan 块:
示例
>>> from sympy import jordan_cell >>> from sympy.abc import x >>> jordan_cell(x, 4) Matrix([ [x, 1, 0, 0], [0, x, 1, 0], [0, 0, x, 1], [0, 0, 0, x]])
- sympy.matrices.dense.hessian(f, varlist, constraints=())[源代码][源代码]¶
计算函数 f 相对于 varlist 中参数的 Hessian 矩阵,varlist 可以是一个序列或行/列向量。可以选择性地给出一个约束列表。
参考文献
示例
>>> from sympy import Function, hessian, pprint >>> from sympy.abc import x, y >>> f = Function('f')(x, y) >>> g1 = Function('g')(x, y) >>> g2 = x**2 + 3*y >>> pprint(hessian(f, (x, y), [g1, g2])) [ d d ] [ 0 0 --(g(x, y)) --(g(x, y)) ] [ dx dy ] [ ] [ 0 0 2*x 3 ] [ ] [ 2 2 ] [d d d ] [--(g(x, y)) 2*x ---(f(x, y)) -----(f(x, y))] [dx 2 dy dx ] [ dx ] [ ] [ 2 2 ] [d d d ] [--(g(x, y)) 3 -----(f(x, y)) ---(f(x, y)) ] [dy dy dx 2 ] [ dy ]
- sympy.matrices.dense.GramSchmidt(vlist, orthonormal=False)[源代码][源代码]¶
对一组向量应用格拉姆-施密特过程。
- 参数:
- vlist矩阵列表
要进行正交化的向量。
- 正交归一布尔值,可选
如果为真,返回一个标准正交基。
- 返回:
- vlist矩阵列表
正交化向量
注释
这个例程大部分与
Matrix.orthogonalize重复,除了一些不同之处,即当发现线性相关向量时,这个例程总是会引发错误,并且关键字normalize在这个函数中被命名为orthonormal。参考文献
- sympy.matrices.dense.wronskian(functions, var, method='bareiss')[源代码][源代码]¶
计算函数 [] 的 Wronskian
| f1 f2 ... fn | | f1' f2' ... fn' | | . . . . | W(f1, ..., fn) = | . . . . | | . . . . | | (n) (n) (n) | | D (f1) D (f2) ... D (fn) |
- sympy.matrices.dense.casoratian(seqs, n, zero=True)[源代码][源代码]¶
给定阶数为 ‘k’ 的线性差分算子 L 和齐次方程 Ly = 0,我们希望计算 L 的核,这是一个由 ‘k’ 个序列组成的集合:a(n), b(n), … z(n)。
L 的解是线性无关的当且仅当它们的 Casoratian,记作 C(a, b, …, z),在 n = 0 时不为零。
Casoratian 由 k x k 行列式定义:
+ a(n) b(n) . . . z(n) + | a(n+1) b(n+1) . . . z(n+1) | | . . . . | | . . . . | | . . . . | + a(n+k-1) b(n+k-1) . . . z(n+k-1) +
它在 rsolve_hyper() 中非常有用,其中它被应用于递归的生成集,以分解出线性相关的解并返回一个基:
>>> from sympy import Symbol, casoratian, factorial >>> n = Symbol('n', integer=True)
指数函数和阶乘函数是线性无关的:
>>> casoratian([2**n, factorial(n)], n) != 0 True
- sympy.matrices.dense.randMatrix(
- r,
- c=None,
- min=0,
- max=99,
- seed=None,
- symmetric=False,
- percent=100,
- prng=None,
创建一个维度为
rxc的随机矩阵。如果省略c,则矩阵为方阵。如果symmetric为 True,则矩阵必须是方阵。如果percent小于 100,则只有大约给定百分比的元素是非零的。用于生成矩阵的伪随机数生成器按以下方式选择。
如果提供了
prng,它将被用作随机数生成器。它应该是random.Random的一个实例,或者至少具有相同签名的randint和shuffle方法。如果未提供
prng但提供了seed,则将使用给定的seed创建新的random.Random。否则,将使用一个默认种子的
random.Random。
示例
>>> from sympy import randMatrix >>> randMatrix(3) [25, 45, 27] [44, 54, 9] [23, 96, 46] >>> randMatrix(3, 2) [87, 29] [23, 37] [90, 26] >>> randMatrix(3, 3, 0, 2) [0, 2, 0] [2, 0, 1] [0, 0, 1] >>> randMatrix(3, symmetric=True) [85, 26, 29] [26, 71, 43] [29, 43, 57] >>> A = randMatrix(3, seed=1) >>> B = randMatrix(3, seed=2) >>> A == B False >>> A == randMatrix(3, seed=1) True >>> randMatrix(3, symmetric=True, percent=50) [77, 70, 0], [70, 0, 0], [ 0, 0, 88]
旋转矩阵¶
- sympy.matrices.dense.rot_givens(i, j, theta, dim=3)[源代码][源代码]¶
返回一个 Givens 旋转矩阵,即在两个坐标轴所张成的平面内的旋转。
- 参数:
- i : 介于
0和dim - 1之间的整数int 之间 表示第一个轴
- j : 介于
0和dim - 1之间的整数int 之间 表示第二轴
- 暗淡int 大于 1
维度数量。默认为3。
- i : 介于
参见
rot_axis1返回一个绕1轴(顺时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis2返回一个绕2轴(顺时针绕y轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis3返回一个绕3轴(顺时针绕z轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis1返回一个绕1轴(逆时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis2返回一个绕2轴(围绕y轴逆时针方向)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis3返回一个绕 3 轴(逆时针绕 z 轴)旋转 theta(以弧度为单位)的旋转矩阵
参考文献
示例
>>> from sympy import pi, rot_givens
绕第三轴(z轴)逆时针旋转 pi/3(60度):
>>> rot_givens(1, 0, pi/3) Matrix([ [ 1/2, -sqrt(3)/2, 0], [sqrt(3)/2, 1/2, 0], [ 0, 0, 1]])
如果我们旋转 pi/2 (90 度):
>>> rot_givens(1, 0, pi/2) Matrix([ [0, -1, 0], [1, 0, 0], [0, 0, 1]])
这可以推广到任意数量的维度:
>>> rot_givens(1, 0, pi/2, dim=4) Matrix([ [0, -1, 0, 0], [1, 0, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])
- sympy.matrices.dense.rot_axis1(theta)[源代码][源代码]¶
返回一个绕1轴旋转theta(以弧度为单位)的旋转矩阵。
参见
rot_givens返回一个 Givens 旋转矩阵(适用于任意维度的广义旋转)
rot_ccw_axis1返回一个绕1轴(逆时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis2返回一个绕2轴(顺时针绕y轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis3返回一个绕3轴(顺时针绕z轴)旋转theta(以弧度为单位)的旋转矩阵
示例
>>> from sympy import pi, rot_axis1
一个 pi/3 (60 度) 的旋转:
>>> theta = pi/3 >>> rot_axis1(theta) Matrix([ [1, 0, 0], [0, 1/2, sqrt(3)/2], [0, -sqrt(3)/2, 1/2]])
如果我们旋转 pi/2 (90 度):
>>> rot_axis1(pi/2) Matrix([ [1, 0, 0], [0, 0, 1], [0, -1, 0]])
- sympy.matrices.dense.rot_axis2(theta)[源代码][源代码]¶
返回一个绕2轴旋转theta(以弧度为单位)的旋转矩阵。
参见
rot_givens返回一个 Givens 旋转矩阵(适用于任意维度的广义旋转)
rot_ccw_axis2返回一个绕2轴(顺时针绕y轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis1返回一个绕1轴(逆时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis3返回一个绕 3 轴(逆时针绕 z 轴)旋转 theta(以弧度为单位)的旋转矩阵
示例
>>> from sympy import pi, rot_axis2
一个 pi/3 (60 度) 的旋转:
>>> theta = pi/3 >>> rot_axis2(theta) Matrix([ [ 1/2, 0, -sqrt(3)/2], [ 0, 1, 0], [sqrt(3)/2, 0, 1/2]])
如果我们旋转 pi/2 (90 度):
>>> rot_axis2(pi/2) Matrix([ [0, 0, -1], [0, 1, 0], [1, 0, 0]])
- sympy.matrices.dense.rot_axis3(theta)[源代码][源代码]¶
返回一个绕 3 轴旋转 theta(以弧度为单位)的旋转矩阵。
参见
rot_givens返回一个 Givens 旋转矩阵(适用于任意维度的广义旋转)
rot_ccw_axis3返回一个绕 3 轴(逆时针绕 z 轴)旋转 theta(以弧度为单位)的旋转矩阵
rot_axis1返回一个绕1轴(顺时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_axis2返回一个绕2轴(顺时针绕y轴)旋转theta(以弧度为单位)的旋转矩阵
示例
>>> from sympy import pi, rot_axis3
一个 pi/3 (60 度) 的旋转:
>>> theta = pi/3 >>> rot_axis3(theta) Matrix([ [ 1/2, sqrt(3)/2, 0], [-sqrt(3)/2, 1/2, 0], [ 0, 0, 1]])
如果我们旋转 pi/2 (90 度):
>>> rot_axis3(pi/2) Matrix([ [ 0, 1, 0], [-1, 0, 0], [ 0, 0, 1]])
- sympy.matrices.dense.rot_ccw_axis1(theta)[源代码][源代码]¶
返回一个绕1轴旋转theta(以弧度为单位)的旋转矩阵。
参见
rot_givens返回一个 Givens 旋转矩阵(适用于任意维度的广义旋转)
rot_axis1返回一个绕1轴(顺时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis2返回一个绕2轴(围绕y轴逆时针方向)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis3返回一个绕 3 轴(逆时针绕 z 轴)旋转 theta(以弧度为单位)的旋转矩阵
示例
>>> from sympy import pi, rot_ccw_axis1
一个 pi/3 (60 度) 的旋转:
>>> theta = pi/3 >>> rot_ccw_axis1(theta) Matrix([ [1, 0, 0], [0, 1/2, -sqrt(3)/2], [0, sqrt(3)/2, 1/2]])
如果我们旋转 pi/2 (90 度):
>>> rot_ccw_axis1(pi/2) Matrix([ [1, 0, 0], [0, 0, -1], [0, 1, 0]])
- sympy.matrices.dense.rot_ccw_axis2(theta)[源代码][源代码]¶
返回一个绕2轴旋转theta(以弧度为单位)的旋转矩阵。
参见
rot_givens返回一个 Givens 旋转矩阵(适用于任意维度的广义旋转)
rot_axis2返回一个绕2轴(顺时针绕y轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis1返回一个绕1轴(逆时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis3返回一个绕 3 轴(逆时针绕 z 轴)旋转 theta(以弧度为单位)的旋转矩阵
示例
>>> from sympy import pi, rot_ccw_axis2
一个 pi/3 (60 度) 的旋转:
>>> theta = pi/3 >>> rot_ccw_axis2(theta) Matrix([ [ 1/2, 0, sqrt(3)/2], [ 0, 1, 0], [-sqrt(3)/2, 0, 1/2]])
如果我们旋转 pi/2 (90 度):
>>> rot_ccw_axis2(pi/2) Matrix([ [ 0, 0, 1], [ 0, 1, 0], [-1, 0, 0]])
- sympy.matrices.dense.rot_ccw_axis3(theta)[源代码][源代码]¶
返回一个绕 3 轴旋转 theta(以弧度为单位)的旋转矩阵。
参见
rot_givens返回一个 Givens 旋转矩阵(适用于任意维度的广义旋转)
rot_axis3返回一个绕3轴(顺时针绕z轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis1返回一个绕1轴(逆时针绕x轴)旋转theta(以弧度为单位)的旋转矩阵
rot_ccw_axis2返回一个绕2轴(围绕y轴逆时针方向)旋转theta(以弧度为单位)的旋转矩阵
示例
>>> from sympy import pi, rot_ccw_axis3
一个 pi/3 (60 度) 的旋转:
>>> theta = pi/3 >>> rot_ccw_axis3(theta) Matrix([ [ 1/2, -sqrt(3)/2, 0], [sqrt(3)/2, 1/2, 0], [ 0, 0, 1]])
如果我们旋转 pi/2 (90 度):
>>> rot_ccw_axis3(pi/2) Matrix([ [0, -1, 0], [1, 0, 0], [0, 0, 1]])
Numpy 实用函数¶
- sympy.matrices.dense.list2numpy(l, dtype=<class 'object'>)[源代码][源代码]¶
将 SymPy 表达式的 Python 列表转换为 NumPy 数组。
参见
- sympy.matrices.dense.symarray(prefix, shape, **kwargs)[源代码][源代码]¶
创建一个包含符号的 numpy ndarray(作为对象数组)。
创建的符号被命名为
prefix_i1_i2_… 因此,如果你希望你的符号对于不同的输出数组是唯一的,你应该提供一个非空的前缀,因为具有相同名称的 SymPy 符号是同一个对象。- 参数:
- 前缀字符串
一个前缀,添加到每个符号的名称前。
- 形状int 或 tuple
创建的数组的形状。如果是一个整数,数组是一维的;对于多维数组,形状必须是一个元组。
- **kwargsdict
传递给 Symbol 的关键字参数
示例
这些文档测试需要 numpy。
>>> from sympy import symarray >>> symarray('', 3) [_0 _1 _2]
如果你想让多个 symarrays 包含不同的符号,你必须提供唯一的 \(前缀\):
>>> a = symarray('', 3) >>> b = symarray('', 3) >>> a[0] == b[0] True >>> a = symarray('a', 3) >>> b = symarray('b', 3) >>> a[0] == b[0] False
使用前缀创建符号数组:
>>> symarray('a', 3) [a_0 a_1 a_2]
对于多维情况,形状必须以元组形式给出:
>>> symarray('a', (2, 3)) [[a_0_0 a_0_1 a_0_2] [a_1_0 a_1_1 a_1_2]] >>> symarray('a', (2, 3, 2)) [[[a_0_0_0 a_0_0_1] [a_0_1_0 a_0_1_1] [a_0_2_0 a_0_2_1]] [[a_1_0_0 a_1_0_1] [a_1_1_0 a_1_1_1] [a_1_2_0 a_1_2_1]]]
对于设定底层符号的假设:
>>> [s.is_real for s in symarray('a', 2, real=True)] [True, True]