使用奇异函数解决梁弯曲问题¶
为了使本文档更易于阅读,请启用漂亮的打印功能:
>>> from sympy import *
>>> x, y, z = symbols('x y z')
>>> init_printing(use_unicode=True)
Beam¶
平面梁是一种结构元件,能够通过内部剪切和弯曲的阻力来承受载荷。梁的特征在于其长度、约束、横截面的惯性矩和弹性模量。在SymPy中,二维梁对象通过指定以下属性来构建:
长度
弹性模量
面积的二次矩
变量 : 表示沿梁长度的位置的符号。默认情况下,这被设置为
Symbol(x)。- 边界条件
bc_slope : 斜率的边界条件。
bc_deflection : 偏转的边界条件。
负载分布
一旦上述内容被指定,以下方法将用于计算加载梁的有用信息:
solve_for_reaction_loads()shear_force()bending_moment()slope()
示例¶
以下是两维梁弯曲问题的多种示例。
示例 1¶
一根长度为9米的悬臂梁,在固定端起5米的距离内施加了一个向下的8 kN/m的均布载荷。在距固定端5米处施加了一个50 kN-m的逆时针力矩。最后,在梁的自由端施加了一个向下的12 kN的点载荷。
y
^
|
\\\\|
\\\\| 8 kN/m
\\\\|_________________
\\\\|| | | | | | | | | 12 kN
\\\\|V V V V V V V V V |
\\\\|________________|_______________V
\\\\| | |
\\\\o - - - - - - - -↺ 50 kN-m - - - | - - -> x
\\\\|________________|_______________|
\\\\| :
\\\\|----------------|---------------|
5.0 m 4.0 m
备注
用户可以自由选择自己的符号约定。在这种情况下,向下的力和逆时针的弯矩为正。
梁必须用长度、弹性模量和面积的二次矩进行初始化。这些量可以是符号或数字。
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> E, I = symbols('E, I')
>>> b = Beam(9, E, I)
使用 apply_load() 方法将三个载荷施加到梁上。该方法支持点力、点矩以及任意阶的多项式分布载荷,即 \(c, cx, cx^2, cx^3, \ldots\)。
12 kN 的点载荷方向为负,位于9米处,多项式阶数指定为 -1:
>>> b.apply_load(12, 9, -1)
然后可以使用 load 属性以奇点函数的形式访问加载函数:
>>> b.load
-1
12⋅<x - 9>
同样地,正弯矩可以通过多项式阶数 -2 来施加:
>>> b.apply_load(50, 5, -2)
分布载荷的阶数为0,范围从x=0到x=5:
>>> b.apply_load(8, 0, 0, end=5)
固定端施加两个边界条件:1) 无垂直挠度和2) 无旋转。这些通过附加x值的元组和相应的挠度或斜率值来指定:
>>> b.bc_deflection.append((0, 0))
>>> b.bc_slope.append((0, 0))
这些边界条件引入了未知的反作用力和力矩,这些反作用力和力矩需要施加在梁上以维持静力平衡:
>>> R, M = symbols('R, M')
>>> b.apply_load(R, 0, -1)
>>> b.apply_load(M, 0, -2)
>>> b.load
-2 -1 0 -2 0 -1
M⋅<x> + R⋅<x> + 8⋅<x> + 50⋅<x - 5> - 8⋅<x - 5> + 12⋅<x - 9>
这两个变量可以根据施加的载荷求解,最终的载荷可以显示出来:
>>> b.solve_for_reaction_loads(R, M)
>>> b.reaction_loads
{M: 158, R: -52}
>>> b.load
-2 -1 0 -2 0 -1
158⋅<x> - 52⋅<x> + 8⋅<x> + 50⋅<x - 5> - 8⋅<x - 5> + 12⋅<x - 9>
此时,梁已完全定义,并且计算了内部的剪力和弯矩:
>>> b.shear_force()
-1 0 1 -1 1 0
- 158⋅<x> + 52⋅<x> - 8⋅<x> - 50⋅<x - 5> + 8⋅<x - 5> - 12⋅<x - 9>
>>> b.bending_moment()
0 1 2 0 2 1
- 158⋅<x> + 52⋅<x> - 4⋅<x> - 50⋅<x - 5> + 4⋅<x - 5> - 12⋅<x - 9>
这些可以通过调用各自的绘图方法来可视化:
>>> b.plot_shear_force()
>>> b.plot_bending_moment()
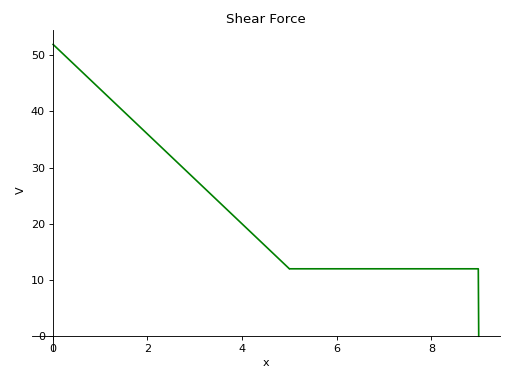
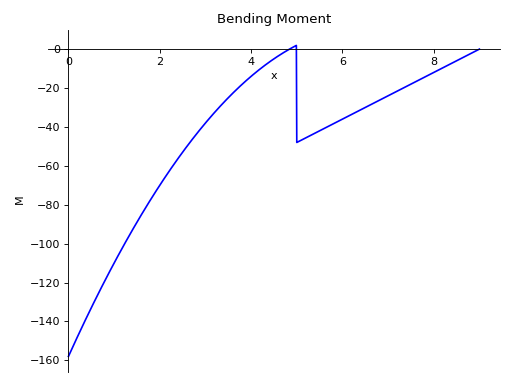
梁在载荷作用下会发生变形,其斜率和挠度可以通过以下公式确定:
>>> b.slope()
⎛ 3 3 ⎞
⎜ 1 2 4⋅<x> 1 4⋅<x - 5> 2⎟
-⎜- 158⋅<x> + 26⋅<x> - ────── - 50⋅<x - 5> + ────────── - 6⋅<x - 9> ⎟
⎝ 3 3 ⎠
─────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 3 4 4 ⎞
⎜ 2 26⋅<x> <x> 2 <x - 5> 3⎟
-⎜- 79⋅<x> + ─────── - ──── - 25⋅<x - 5> + ──────── - 2⋅<x - 9> ⎟
⎝ 3 3 3 ⎠
────────────────────────────────────────────────────────────────────
E⋅I
只要提供了模量和二次矩的数值,就可以绘制梁的斜率和挠度:
>>> b.plot_slope(subs={E: 20E9, I: 3.25E-6})
>>> b.plot_deflection(subs={E: 20E9, I: 3.25E-6})
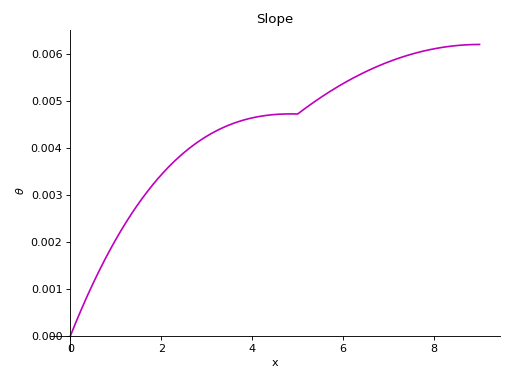
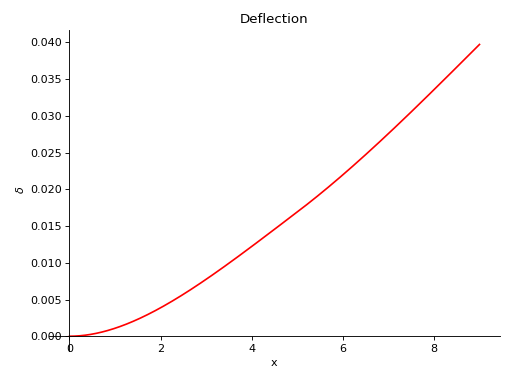
所有的图表都可以在一个图中显示,使用:
>>> b.plot_loading_results(subs={E: 20E9, I: 3.25E-6})
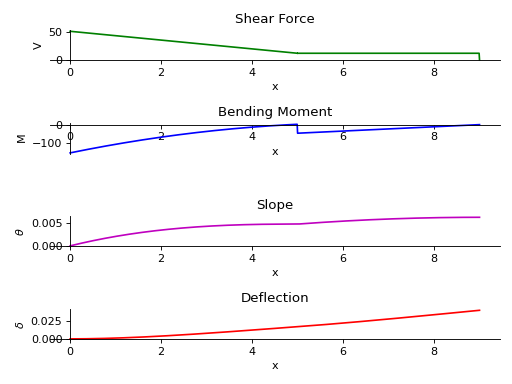
示例 2¶
有一根长度为30米的梁。在梁的末端施加了一个大小为120 Nm的逆时针方向的力矩。在梁的起始点从顶部施加了一个大小为8 N的点载荷。梁下方有两个简单的支撑。一个在末端,另一个在距离起点10米处。两个支撑处的挠度都被限制。
|| 8 N ↺ 120 Nm
\/______________________________________________|
|_______________________________________________|
/\ /\
|------------|---------------------------------|
10 m 20 m
备注
使用向下力和逆时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> R1, R2 = symbols('R1, R2')
>>> b = Beam(30, E, I)
>>> b.apply_load(8, 0, -1)
>>> b.apply_load(R1, 10, -1)
>>> b.apply_load(R2, 30, -1)
>>> b.apply_load(120, 30, -2)
>>> b.bc_deflection.append((10, 0))
>>> b.bc_deflection.append((30, 0))
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: -18, R₂: 10}
>>> b.load
-1 -1 -2 -1
8⋅<x> - 18⋅<x - 10> + 120⋅<x - 30> + 10⋅<x - 30>
>>> b.shear_force()
0 0 -1 0
- 8⋅<x> + 18⋅<x - 10> - 120⋅<x - 30> - 10⋅<x - 30>
>>> b.bending_moment()
1 1 0 1
- 8⋅<x> + 18⋅<x - 10> - 120⋅<x - 30> - 10⋅<x - 30>
>>> b.slope()
2 2 1 2 1600
4⋅<x> - 9⋅<x - 10> + 120⋅<x - 30> + 5⋅<x - 30> - ────
3
─────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3 3
1600⋅x 4⋅<x> 3 2 5⋅<x - 30>
- ────── + ────── - 3⋅<x - 10> + 60⋅<x - 30> + ─────────── + 4000
3 3 3
───────────────────────────────────────────────────────────────────
E⋅I
示例 3¶
一根长度为6米的梁,在起点处有一个滚轴支座,在终点处有一个铰支座。在梁的中点处施加了一个1.5 kN-m的逆时针力矩。从梁的中点到终点施加了一个3 kN/m的恒定分布载荷和一个1 kN/m/m的斜坡载荷。
ramp load = 1 KN/m/m
constant load = 3 KN/m
|------------------------|
↺ 1.5 KN-m
______________________|________________________
|_______________________________________________|
o | /\
|----------------------|-----------------------|
3.0 m 3.0 m
备注
使用向下力和逆时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols, plot, S
>>> E, I = symbols('E, I')
>>> R1, R2 = symbols('R1, R2')
>>> b = Beam(6, E, I)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(-S(3)/2, 3, -2)
>>> b.apply_load(3, 3, 0)
>>> b.apply_load(1, 3, 1)
>>> b.apply_load(R2, 6, -1)
>>> b.bc_deflection.append((0, 0))
>>> b.bc_deflection.append((6, 0))
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: -11/4, R₂: -43/4}
>>> b.load
-1 -2 -1
11⋅<x> 3⋅<x - 3> 0 1 43⋅<x - 6>
- ──────── - ─────────── + 3⋅<x - 3> + <x - 3> - ────────────
4 2 4
>>> plot(b.load)
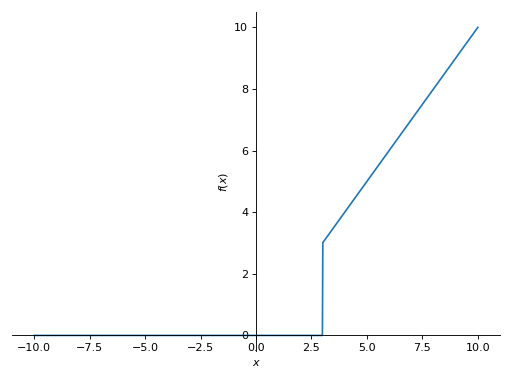
>>> b.shear_force()
0 -1 2 0
11⋅<x> 3⋅<x - 3> 1 <x - 3> 43⋅<x - 6>
─────── + ─────────── - 3⋅<x - 3> - ──────── + ───────────
4 2 2 4
>>> b.bending_moment()
1 0 2 3 1
11⋅<x> 3⋅<x - 3> 3⋅<x - 3> <x - 3> 43⋅<x - 6>
─────── + ────────── - ────────── - ──────── + ───────────
4 2 2 6 4
>>> b.slope()
2 1 3 4 2
11⋅<x> 3⋅<x - 3> <x - 3> <x - 3> 43⋅<x - 6> 78
- ─────── - ────────── + ──────── + ──────── - ─────────── + ──
8 2 2 24 8 5
───────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3 2 4 5 3
78⋅x 11⋅<x> 3⋅<x - 3> <x - 3> <x - 3> 43⋅<x - 6>
──── - ─────── - ────────── + ──────── + ──────── - ───────────
5 24 4 8 120 24
───────────────────────────────────────────────────────────────
E⋅I
示例 4¶
一根悬臂梁长度为8米,在距起点1米处固定,并在另一端前1米处由滚轮支撑。它承受从起点开始到距起点2米处的10 KN/m的均布载荷。在距起点5米和7.5米处分别施加了20KN和8KN的点载荷。
---> x
|
v y
10 KN/m
_____________ 20 KN 8 KN
| | | | | | | | |
V V V V V V V V V
_______________________________________________
|_______________________________________________|
/\ O
|-----|------|-----------------|----------|--|--|
1m 1m 3m 2m .5m .5m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E,I,M,V = symbols('E I M V')
>>> b = Beam(8, E, I)
>>> E,I,R1,R2 = symbols('E I R1 R2')
>>> b.apply_load(R1, 1, -1)
>>> b.apply_load(R2, 7, -1)
>>> b.apply_load(10, 0, 0, end=2)
>>> b.apply_load(20, 5, -1)
>>> b.apply_load(8, 7.5, -1)
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: -26, R₂: -22}
>>> b.load
0 -1 0 -1 -1 -1
10⋅<x> - 26⋅<x - 1> - 10⋅<x - 2> + 20⋅<x - 5> - 22⋅<x - 7> + 8⋅<x - 7.5>
>>> b.shear_force()
1 0 1 0 0 0
- 10⋅<x> + 26⋅<x - 1> + 10⋅<x - 2> - 20⋅<x - 5> + 22⋅<x - 7> - 8⋅<x - 7.5>
>>> b.bending_moment()
2 1 2 1 1 1
- 5⋅<x> + 26⋅<x - 1> + 5⋅<x - 2> - 20⋅<x - 5> + 22⋅<x - 7> - 8⋅<x - 7.5>
>>> b.bc_deflection = [(1, 0), (7, 0)]
>>> b.slope()
3 3
5⋅<x> 2 5⋅<x - 2> 2 2 2 679
────── - 13⋅<x - 1> - ────────── + 10⋅<x - 5> - 11⋅<x - 7> + 4⋅<x - 7.5> + ───
3 3 24
──────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
4 3 4 3 3 3
679⋅x 5⋅<x> 13⋅<x - 1> 5⋅<x - 2> 10⋅<x - 5> 11⋅<x - 7> 4⋅<x - 7.5> 689
───── + ────── - ─────────── - ────────── + ─────────── - ─────────── + ──────────── - ───
24 12 3 12 3 3 3 24
──────────────────────────────────────────────────────────────────────────────────────────
E⋅I
示例 5¶
一根长度为6米的悬臂梁承受着从起点开始到距离起点2米处的向下均匀分布载荷,载荷大小为4.0 kN/m。从梁的中点到末端施加了一个斜坡载荷,大小为1 kN/m/m。在距离起点4米处还施加了一个12 kN的点载荷,方向相同。
---> x .
| . |
v y 12 KN . | |
| . | | |
V . | | | |
\\\\| 4 KN/m . | | | | |
\\\\|___________ . 1 KN/m/m| |
\\\\|| | | | | | . V V V V V V V
\\\\|V V V V V V |---------------|
\\\\|________________________________
\\\\|________________________________|
\\\\| : : :
\\\\|----------|-----|----|----------|
2.0 m 1m 1m 2.0 m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E,I,M,V = symbols('E I M V')
>>> b = Beam(6, E, I)
>>> b.apply_load(V, 0, -1)
>>> b.apply_load(M, 0, -2)
>>> b.apply_load(4, 0, 0, end=2)
>>> b.apply_load(12, 4, -1)
>>> b.apply_load(1, 3, 1, end=6)
>>> b.solve_for_reaction_loads(V, M)
>>> b.reaction_loads
{M: 157/2, V: -49/2}
>>> b.load
-2 -1
157⋅<x> 49⋅<x> 0 0 1 -1 0 1
───────── - ──────── + 4⋅<x> - 4⋅<x - 2> + <x - 3> + 12⋅<x - 4> - 3⋅<x - 6> - <x - 6>
2 2
>>> b.shear_force()
-1 0 2 2
157⋅<x> 49⋅<x> 1 1 <x - 3> 0 1 <x - 6>
- ───────── + ─────── - 4⋅<x> + 4⋅<x - 2> - ──────── - 12⋅<x - 4> + 3⋅<x - 6> + ────────
2 2 2 2
>>> b.bending_moment()
0 1 3 2 3
157⋅<x> 49⋅<x> 2 2 <x - 3> 1 3⋅<x - 6> <x - 6>
- ──────── + ─────── - 2⋅<x> + 2⋅<x - 2> - ──────── - 12⋅<x - 4> + ────────── + ────────
2 2 6 2 6
>>> b.bc_deflection = [(0, 0)]
>>> b.bc_slope = [(0, 0)]
>>> b.slope()
⎛ 1 2 3 3 4 3 4⎞
⎜ 157⋅<x> 49⋅<x> 2⋅<x> 2⋅<x - 2> <x - 3> 2 <x - 6> <x - 6> ⎟
-⎜- ──────── + ─────── - ────── + ────────── - ──────── - 6⋅<x - 4> + ──────── + ────────⎟
⎝ 2 4 3 3 24 2 24 ⎠
────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 2 3 4 4 5 4 5⎞
⎜ 157⋅<x> 49⋅<x> <x> <x - 2> <x - 3> 3 <x - 6> <x - 6> ⎟
-⎜- ──────── + ─────── - ──── + ──────── - ──────── - 2⋅<x - 4> + ──────── + ────────⎟
⎝ 4 12 6 6 120 8 120 ⎠
────────────────────────────────────────────────────────────────────────────────────────
E⋅I
示例 6¶
一根悬臂梁长度为11米,从起点2米处到6米处受到2 KN/m的均布荷载。它在起点处铰接,并在距该端8米处放置在滚轮上。此外,在悬臂端施加了一个5 KN-m的逆时针力矩。
2 KN/m ---> x
_________________ |
| | | | | | | | | v y
V V V V V V V V V ↺ 5 KN-m
____________________________________________________|
O____________________________________________________|
/ \ /\
|--------|----------------|----------|---------------|
2m 4m 2m 3m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> R1, R2 = symbols('R1, R2')
>>> E, I = symbols('E, I')
>>> b = Beam(11, E, I)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(2, 2, 0, end=6)
>>> b.apply_load(R2, 8, -1)
>>> b.apply_load(5, 11, -2)
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.reaction_loads
{R₁: -37/8, R₂: -27/8}
>>> b.load
-1 -1
37⋅<x> 0 0 27⋅<x - 8> -2
- ──────── + 2⋅<x - 2> - 2⋅<x - 6> - ──────────── + 5⋅<x - 11>
8 8
>>> b.shear_force()
0 0
37⋅<x> 1 1 27⋅<x - 8> -1
─────── - 2⋅<x - 2> + 2⋅<x - 6> + ─────────── - 5⋅<x - 11>
8 8
>>> b.bending_moment()
1 1
37⋅<x> 2 2 27⋅<x - 8> 0
─────── - <x - 2> + <x - 6> + ─────────── - 5⋅<x - 11>
8 8
>>> b.bc_deflection = [(0, 0), (8, 0)]
>>> b.slope()
2 3 3 2
37⋅<x> <x - 2> <x - 6> 27⋅<x - 8> 1
- ─────── + ──────── - ──────── - ─────────── + 5⋅<x - 11> + 36
16 3 3 16
────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
3 4 4 3 2
37⋅<x> <x - 2> <x - 6> 9⋅<x - 8> 5⋅<x - 11>
36⋅x - ─────── + ──────── - ──────── - ────────── + ───────────
48 12 12 16 2
───────────────────────────────────────────────────────────────
E⋅I
示例 7¶
存在一根长度为 l 的梁,两端固定。在梁的中点处施加一个大小为 F 的集中点载荷,方向向下。
^ y
|
---> x
\\\\| F |\\\\
\\\\| | |\\\\
\\\\| V |\\\\
\\\\|_____________________________________|\\\\
\\\\|_____________________________________|\\\\
\\\\| : |\\\\
\\\\| : |\\\\
\\\\|------------------|------------------|\\\\
l/2 l/2
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I, F = symbols('E I F')
>>> l = symbols('l', positive=True)
>>> b = Beam(l, E, I)
>>> R1,R2 = symbols('R1 R2')
>>> M1, M2 = symbols('M1, M2')
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(M1, 0, -2)
>>> b.apply_load(R2, l, -1)
>>> b.apply_load(M2, l, -2)
>>> b.apply_load(-F, l/2, -1)
>>> b.bc_deflection = [(0, 0),(l, 0)]
>>> b.bc_slope = [(0, 0),(l, 0)]
>>> b.solve_for_reaction_loads(R1, R2, M1, M2)
>>> b.reaction_loads
⎧ -F⋅l F⋅l F F⎫
⎨M₁: ─────, M₂: ───, R₁: ─, R₂: ─⎬
⎩ 8 8 2 2⎭
>>> b.load
-2 -2 -1 -1 -1
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> l F⋅<-l + x>
- ───────── + ────────────── + ─────── - F⋅<- ─ + x> + ────────────
8 8 2 2 2
>>> b.shear_force()
-1 -1 0 0 0
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> l F⋅<-l + x>
───────── - ────────────── - ────── + F⋅<- ─ + x> - ───────────
8 8 2 2 2
>>> b.bending_moment()
0 0 1 1 1
F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> l F⋅<-l + x>
──────── - ───────────── - ────── + F⋅<- ─ + x> - ───────────
8 8 2 2 2
>>> b.slope()
⎛ 2 ⎞
⎜ l ⎟
⎜ 1 1 2 F⋅<- ─ + x> 2⎟
⎜F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> 2 F⋅<-l + x> ⎟
-⎜──────── - ───────────── - ────── + ──────────── - ───────────⎟
⎝ 8 8 4 2 4 ⎠
──────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 3 ⎞
⎜ l ⎟
⎜ 2 2 3 F⋅<- ─ + x> 3⎟
⎜F⋅l⋅<x> F⋅l⋅<-l + x> F⋅<x> 2 F⋅<-l + x> ⎟
-⎜──────── - ───────────── - ────── + ──────────── - ───────────⎟
⎝ 16 16 12 6 12 ⎠
──────────────────────────────────────────────────────────────────
E⋅I
示例 8¶
存在一根长度为 4*l 的梁,中间有一个铰链连接器。它在起点处有一个固定支撑,并且在距离起点 l 和 4*l 处有两个滚轮。在距离起点 3*l 处还施加了一个集中点载荷 P。
---> x
\\\\| P |
\\\\| | v y
\\\\| V
\\\\|_____________________ _______________________
\\\\|_____________________O_______________________|
\\\\| /\ : /\
\\\\| oooo : oooo
\\\\|----------|-----------|----------|-----------|
l l l l
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E I')
>>> l = symbols('l', positive=True)
>>> R1, M1, R2, R3, P = symbols('R1 M1 R2 R3 P')
>>> b1 = Beam(2*l, E, I)
>>> b2 = Beam(2*l, E, I)
>>> b = b1.join(b2, "hinge")
>>> b.apply_load(M1, 0, -2)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(R2, l, -1)
>>> b.apply_load(R3, 4*l, -1)
>>> b.apply_load(P, 3*l, -1)
>>> b.bc_slope = [(0, 0)]
>>> b.bc_deflection = [(0, 0), (l, 0), (4*l, 0)]
>>> b.solve_for_reaction_loads(M1, R1, R2, R3)
>>> b.reaction_loads
⎧ -P⋅l 3⋅P -5⋅P -P ⎫
⎨M₁: ─────, R₁: ───, R₂: ─────, R₃: ───⎬
⎩ 4 4 4 2 ⎭
>>> b.load
2 -3 -2 -1 -1 -1
13⋅P⋅l ⋅<-2⋅l + x> P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> -1 P⋅<-4⋅l + x>
- ──────────────────── - ───────── + ───────── - ────────────── + P⋅<-3⋅l + x> - ──────────────
48 4 4 4 2
>>> b.shear_force()
2 -2 -1 0 0 0
13⋅P⋅l ⋅<-2⋅l + x> P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> 0 P⋅<-4⋅l + x>
──────────────────── + ───────── - ──────── + ───────────── - P⋅<-3⋅l + x> + ─────────────
48 4 4 4 2
>>> b.bending_moment()
2 -1 0 1 1 1
13⋅P⋅l ⋅<-2⋅l + x> P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> 1 P⋅<-4⋅l + x>
──────────────────── + ──────── - ──────── + ───────────── - P⋅<-3⋅l + x> + ─────────────
48 4 4 4 2
>>> b.slope()
⎛ 2 0 1 2 2 2 2⎞
⎜13⋅P⋅l ⋅<-2⋅l + x> P⋅l⋅<x> 3⋅P⋅<x> 5⋅P⋅<-l + x> P⋅<-3⋅l + x> P⋅<-4⋅l + x> ⎟
-⎜─────────────────── + ──────── - ──────── + ───────────── - ───────────── + ─────────────⎟
⎝ 48 4 8 8 2 4 ⎠
─────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 2 1 2 3 3 3 3⎞
⎜13⋅P⋅l ⋅<-2⋅l + x> P⋅l⋅<x> P⋅<x> 5⋅P⋅<-l + x> P⋅<-3⋅l + x> P⋅<-4⋅l + x> ⎟
-⎜─────────────────── + ──────── - ────── + ───────────── - ───────────── + ─────────────⎟
⎝ 48 8 8 24 6 12 ⎠
───────────────────────────────────────────────────────────────────────────────────────────
E⋅I
示例 9¶
有一个长度为4米的悬臂梁。前2米的惯性矩为 1.5*I,其余部分为 I。在其自由端顶部施加了一个大小为20 N的点载荷。
---> x
\\\\| |
\\\\| 20 N v y
\\\\|________________ |
\\\\| |_______________V
\\\\| 1.5*I _______I_______|
\\\\|________________|
\\\\| :
\\\\|----------------|---------------|
2.0 m 2.0 m
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> R1, R2 = symbols('R1, R2')
>>> b1 = Beam(2, E, 1.5*I)
>>> b2 = Beam(2, E, I)
>>> b = b1.join(b2, "fixed")
>>> b.apply_load(20, 4, -1)
>>> b.apply_load(R1, 0, -1)
>>> b.apply_load(R2, 0, -2)
>>> b.bc_slope = [(0, 0)]
>>> b.bc_deflection = [(0, 0)]
>>> b.solve_for_reaction_loads(R1, R2)
>>> b.load
-2 -1 -1
80⋅<x> - 20⋅<x> + 20⋅<x - 4>
>>> b.shear_force()
-1 0 0
- 80⋅<x> + 20⋅<x> - 20⋅<x - 4>
>>> b.bending_moment()
0 1 1
- 80⋅<x> + 20⋅<x> - 20⋅<x - 4>
>>> b.slope()
⎛ 1 2 2 ⎞
⎜ - 80⋅<x> + 10⋅<x> - 10⋅<x - 4> 120 ⎟
⎜ ───────────────────────────────── + ─── ⎟ ⎛ 1 2 2⎞ 0 ⎛ 1 2 2⎞ 0
⎜ I I 80.0⎟ 0 0.666666666666667⋅⎝- 80⋅<x> + 10⋅<x> - 10⋅<x - 4> ⎠⋅<x> 0.666666666666667⋅⎝- 80⋅<x> + 10⋅<x> - 10⋅<x - 4> ⎠⋅<x - 2>
⎜- ─────────────────────────────────────── + ────⎟⋅<x - 2> - ────────────────────────────────────────────────────────── + ──────────────────────────────────────────────────────────────
⎝ E E⋅I ⎠ E⋅I E⋅I
示例 10¶
一个具有恒定弯曲刚度 E*I 的组合梁,由长度为 2*l 的梁连接到长度为 l 的梁的右侧形成。整个梁的两端都是固定的。在距起点 2*l 的距离处,还从顶部施加了一个大小为 P 的点载荷。
---> x
|
\\\\| P v y |\\\\
\\\\| | |\\\\
\\\\| V |\\\\
\\\\|____________ ________________________|\\\\
\\\\|____________O________________________|\\\\
\\\\| : : |\\\\
\\\\| : : |\\\\
\\\\|------------|------------|-----------|\\\\
l l l
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> l = symbols('l', positive=True)
>>> b1 = Beam(l ,E,I)
>>> b2 = Beam(2*l ,E,I)
>>> b = b1.join(b2,"hinge")
>>> M1, A1, M2, A2, P = symbols('M1 A1 M2 A2 P')
>>> b.apply_load(A1, 0, -1)
>>> b.apply_load(M1, 0 ,-2)
>>> b.apply_load(P, 2*l, -1)
>>> b.apply_load(A2, 3*l, -1)
>>> b.apply_load(M2, 3*l, -2)
>>> b.bc_slope=[(0, 0), (3*l, 0)]
>>> b.bc_deflection=[(0, 0), (3*l, 0)]
>>> b.solve_for_reaction_loads(M1, A1, M2, A2)
>>> b.reaction_loads
⎧ -5⋅P -13⋅P 5⋅P⋅l -4⋅P⋅l ⎫
⎨A₁: ─────, A₂: ──────, M₁: ─────, M₂: ───────⎬
⎩ 18 18 18 9 ⎭
>>> b.load
2 -3 -2 -2 -1 -1
P⋅l ⋅<-l + x> 5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> -1 13⋅P⋅<-3⋅l + x>
- ─────────────── + ─────────── - ────────────────── - ───────── + P⋅<-2⋅l + x> - ─────────────────
12 18 9 18 18
>>> b.shear_force()
2 -2 -1 -1 0 0
P⋅l ⋅<-l + x> 5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> 0 13⋅P⋅<-3⋅l + x>
─────────────── - ─────────── + ────────────────── + ──────── - P⋅<-2⋅l + x> + ────────────────
12 18 9 18 18
>>> b.bending_moment()
2 -1 0 0 1 1
P⋅l ⋅<-l + x> 5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> 1 13⋅P⋅<-3⋅l + x>
─────────────── - ────────── + ───────────────── + ──────── - P⋅<-2⋅l + x> + ────────────────
12 18 9 18 18
>>> b.slope()
⎛ 2 0 1 1 2 2 2⎞
⎜P⋅l ⋅<-l + x> 5⋅P⋅l⋅<x> 4⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> P⋅<-2⋅l + x> 13⋅P⋅<-3⋅l + x> ⎟
-⎜────────────── - ────────── + ───────────────── + ──────── - ───────────── + ────────────────⎟
⎝ 12 18 9 36 2 36 ⎠
─────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 2 1 2 2 3 3 3⎞
⎜P⋅l ⋅<-l + x> 5⋅P⋅l⋅<x> 2⋅P⋅l⋅<-3⋅l + x> 5⋅P⋅<x> P⋅<-2⋅l + x> 13⋅P⋅<-3⋅l + x> ⎟
-⎜────────────── - ────────── + ───────────────── + ──────── - ───────────── + ────────────────⎟
⎝ 12 36 9 108 6 108 ⎠
─────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
示例 11¶
任何由多项式定义的载荷都可以施加到梁上。这允许近似任意载荷分布。以下示例显示了在梁表面上的六个截断多项式载荷。
>>> n = 6
>>> b = Beam(10*n, E, I)
>>> for i in range(n):
... b.apply_load(1 / (5**i), 10*i + 5, i, end=10*i + 10)
>>> plot(b.load, (x, 0, 10*n))
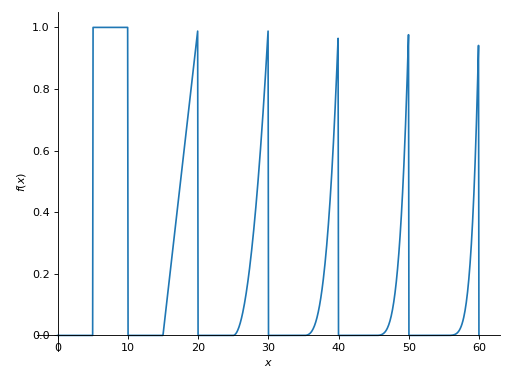
示例 12¶
与示例10相同的Beam形式,但使用 apply_rotation_hinge() 和 apply_support() 方法。
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols
>>> E, I = symbols('E, I')
>>> l = symbols('l', positive=True)
>>> b = Beam(3*l, E, I)
>>> r0,m0 = b.apply_support(0, type='fixed')
>>> r3l,m3l = b.apply_support(3*l, type='fixed')
>>> F = symbols('F')
>>> p1 = b.apply_rotation_hinge(l)
>>> b.apply_load(F, 2*l, -1)
>>> b.solve_for_reaction_loads(r0,m0,r3l,m3l)
>>> b.reaction_loads
⎧ 5⋅F⋅l -4⋅F⋅l -5⋅F -13⋅F ⎫
⎨M₀: ─────, M_3*l: ───────, R₀: ─────, R_3*l: ──────⎬
⎩ 18 9 18 18 ⎭
>>> b.load
2 -3 -2 -2 -1 -1
F⋅l ⋅<-l + x> 5⋅F⋅l⋅<x> 4⋅F⋅l⋅<-3⋅l + x> 5⋅F⋅<x> -1 13⋅F⋅<-3⋅l + x>
- ─────────────── + ─────────── - ────────────────── - ───────── + F⋅<-2⋅l + x> - ─────────────────
12 18 9 18 18
>>> b.shear_force()
2 -2 -1 -1 0 0
F⋅l ⋅<-l + x> 5⋅F⋅l⋅<x> 4⋅F⋅l⋅<-3⋅l + x> 5⋅F⋅<x> 0 13⋅F⋅<-3⋅l + x>
─────────────── - ─────────── + ────────────────── + ──────── - F⋅<-2⋅l + x> + ────────────────
12 18 9 18 18
>>> b.bending_moment()
2 -1 0 0 1 1
F⋅l ⋅<-l + x> 5⋅F⋅l⋅<x> 4⋅F⋅l⋅<-3⋅l + x> 5⋅F⋅<x> 1 13⋅F⋅<-3⋅l + x>
─────────────── - ────────── + ───────────────── + ──────── - F⋅<-2⋅l + x> + ────────────────
12 18 9 18 18
>>> b.slope()
⎛ 2 0 1 1 2 2 2⎞
⎜F⋅l ⋅<-l + x> 5⋅F⋅l⋅<x> 4⋅F⋅l⋅<-3⋅l + x> 5⋅F⋅<x> F⋅<-2⋅l + x> 13⋅F⋅<-3⋅l + x> ⎟
-⎜────────────── - ────────── + ───────────────── + ──────── - ───────────── + ────────────────⎟
⎝ 12 18 9 36 2 36 ⎠
─────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 2 1 2 2 3 3 3⎞
⎜F⋅l ⋅<-l + x> 5⋅F⋅l⋅<x> 2⋅F⋅l⋅<-3⋅l + x> 5⋅F⋅<x> F⋅<-2⋅l + x> 13⋅F⋅<-3⋅l + x> ⎟
-⎜────────────── - ────────── + ───────────────── + ──────── - ───────────── + ────────────────⎟
⎝ 12 36 9 108 6 108 ⎠
─────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
示例 13¶
有一根长度为 3*l 的梁固定在两端。在 l/3 处施加了一个载荷,在 2*l 和 3*l 之间施加了一个分布载荷 q1。梁在 l*5/2 处有一个滑动铰链,使用 apply_sliding_hinge() 方法实现。
备注
可以使用 l*5/2 作为输入,但使用 Rational(5, 2) 是更好的做法。这有助于求解器将输入理解为分数,并输出精确解而不是浮点数。
>>> from sympy.physics.continuum_mechanics.beam import Beam
>>> from sympy import symbols, Rational
>>> E, I = symbols('E, I')
>>> l = symbols('l', positive=True)
>>> b = Beam(3*l, E, I)
>>> r0, m0 = b.apply_support(0, type='fixed')
>>> r3l, m3l = b.apply_support(3*l, type='fixed')
>>> s1 = b.apply_sliding_hinge(l*Rational(5, 2))
>>> P1, q1 = symbols('P1 q1')
>>> b.apply_load(P1, l*Rational(1, 3), -1)
>>> b.apply_load(q1, 2*l, 0, 3*l)
>>> b.solve_for_reaction_loads(r0, r3l, m0, m3l)
>>> b.reaction_loads
⎧ 2 2 ⎫
⎪ 17⋅P₁⋅l 25⋅l ⋅q₁ P₁⋅l 11⋅l ⋅q₁ l⋅q₁ -l⋅q₁ ⎪
⎨M₀: ─────── + ────────, M_3*l: ──── + ────────, R₀: -P₁ - ────, R_3*l: ──────⎬
⎪ 54 36 54 36 2 2 ⎪
⎩ ⎭
>>> b.load
-4
⎛ 3 4 ⎞ 5⋅l
-1 -1 ⎛ 2 ⎞ ⎛ 2 ⎞ ⎝- 25⋅P₁⋅l - 297⋅l ⋅q₁⎠⋅<- ─── + x>
l l⋅q₁⋅<-3⋅l + x> 0 0 ⎛ l⋅q₁⎞ -1 ⎜P₁⋅l 11⋅l ⋅q₁⎟ -2 ⎜17⋅P₁⋅l 25⋅l ⋅q₁⎟ -2 2
P₁⋅<- ─ + x> - ───────────────── + q₁⋅<-2⋅l + x> - q₁⋅<-3⋅l + x> + ⎜-P₁ - ────⎟⋅<x> + ⎜──── + ────────⎟⋅<-3⋅l + x> + ⎜─────── + ────────⎟⋅<x> + ──────────────────────────────────────
3 2 ⎝ 2 ⎠ ⎝ 54 36 ⎠ ⎝ 54 36 ⎠ 324
>>> b.shear_force()
0 0 ⎛ 2 ⎞ ⎛ 2 ⎞ ⎛ 3 4 ⎞ -3
l l⋅q₁⋅<-3⋅l + x> 1 1 ⎛ l⋅q₁⎞ 0 ⎜P₁⋅l 11⋅l ⋅q₁⎟ -1 ⎜17⋅P₁⋅l 25⋅l ⋅q₁⎟ -1 ⎜ 25⋅P₁⋅l 11⋅l ⋅q₁⎟ 5⋅l
- P₁⋅<- ─ + x> + ──────────────── - q₁⋅<-2⋅l + x> + q₁⋅<-3⋅l + x> - ⎜-P₁ - ────⎟⋅<x> - ⎜──── + ────────⎟⋅<-3⋅l + x> - ⎜─────── + ────────⎟⋅<x> - ⎜- ──────── - ────────⎟⋅<- ─── + x>
3 2 ⎝ 2 ⎠ ⎝ 54 36 ⎠ ⎝ 54 36 ⎠ ⎝ 324 12 ⎠ 2
>>> b.bending_moment()
1 1 2 2 ⎛ 2 ⎞ ⎛ 2 ⎞ ⎛ 3 4 ⎞ -2
l l⋅q₁⋅<-3⋅l + x> q₁⋅<-2⋅l + x> q₁⋅<-3⋅l + x> ⎛ l⋅q₁⎞ 1 ⎜ 17⋅P₁⋅l 25⋅l ⋅q₁⎟ 0 ⎜ P₁⋅l 11⋅l ⋅q₁⎟ 0 ⎜25⋅P₁⋅l 11⋅l ⋅q₁⎟ 5⋅l
- P₁⋅<- ─ + x> + ──────────────── - ────────────── + ────────────── + ⎜P₁ + ────⎟⋅<x> + ⎜- ─────── - ────────⎟⋅<x> + ⎜- ──── - ────────⎟⋅<-3⋅l + x> + ⎜──────── + ────────⎟⋅<- ─── + x>
3 2 2 2 ⎝ 2 ⎠ ⎝ 54 36 ⎠ ⎝ 54 36 ⎠ ⎝ 324 12 ⎠ 2
>>> b.slope()
⎛ -1 2 -1 ⎞
⎜ 3 5⋅l l 4 5⋅l ⎟
⎜25⋅P₁⋅l ⋅<- ─── + x> 1 1 2 P₁⋅<- ─ + x> 11⋅l ⋅q₁⋅<- ─── + x> 2 1 2 1 2 2 3 3⎟
⎜ 2 17⋅P₁⋅l⋅<x> P₁⋅l⋅<-3⋅l + x> P₁⋅<x> 3 2 25⋅l ⋅q₁⋅<x> 11⋅l ⋅q₁⋅<-3⋅l + x> l⋅q₁⋅<x> l⋅q₁⋅<-3⋅l + x> q₁⋅<-2⋅l + x> q₁⋅<-3⋅l + x> ⎟
-⎜────────────────────── - ──────────── - ──────────────── + ─────── - ───────────── + ────────────────────── - ───────────── - ──────────────────── + ───────── + ──────────────── - ────────────── + ──────────────⎟
⎝ 324 54 54 2 2 12 36 36 4 4 6 6 ⎠
───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I
>>> b.deflection()
⎛ 0 3 0 ⎞
⎜ 3 5⋅l l 4 5⋅l ⎟
⎜25⋅P₁⋅l ⋅<- ─── + x> 2 2 3 P₁⋅<- ─ + x> 11⋅l ⋅q₁⋅<- ─── + x> 2 2 2 2 3 3 4 4⎟
⎜ 2 17⋅P₁⋅l⋅<x> P₁⋅l⋅<-3⋅l + x> P₁⋅<x> 3 2 25⋅l ⋅q₁⋅<x> 11⋅l ⋅q₁⋅<-3⋅l + x> l⋅q₁⋅<x> l⋅q₁⋅<-3⋅l + x> q₁⋅<-2⋅l + x> q₁⋅<-3⋅l + x> ⎟
-⎜───────────────────── - ──────────── - ──────────────── + ─────── - ───────────── + ───────────────────── - ───────────── - ──────────────────── + ───────── + ──────────────── - ────────────── + ──────────────⎟
⎝ 324 108 108 6 6 12 72 72 12 12 24 24 ⎠
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
E⋅I