Beam (文档字符串)¶
该模块可用于使用力学中的奇异函数解决二维梁弯曲问题。
- class sympy.physics.continuum_mechanics.beam.Beam(
- length,
- elastic_modulus,
- second_moment,
- area=A,
- variable=x,
- base_char='C',
- ild_variable=a,
梁是一种结构构件,主要通过抵抗弯曲来承受载荷。梁的特点在于其横截面轮廓(惯性矩)、长度和材料。
备注
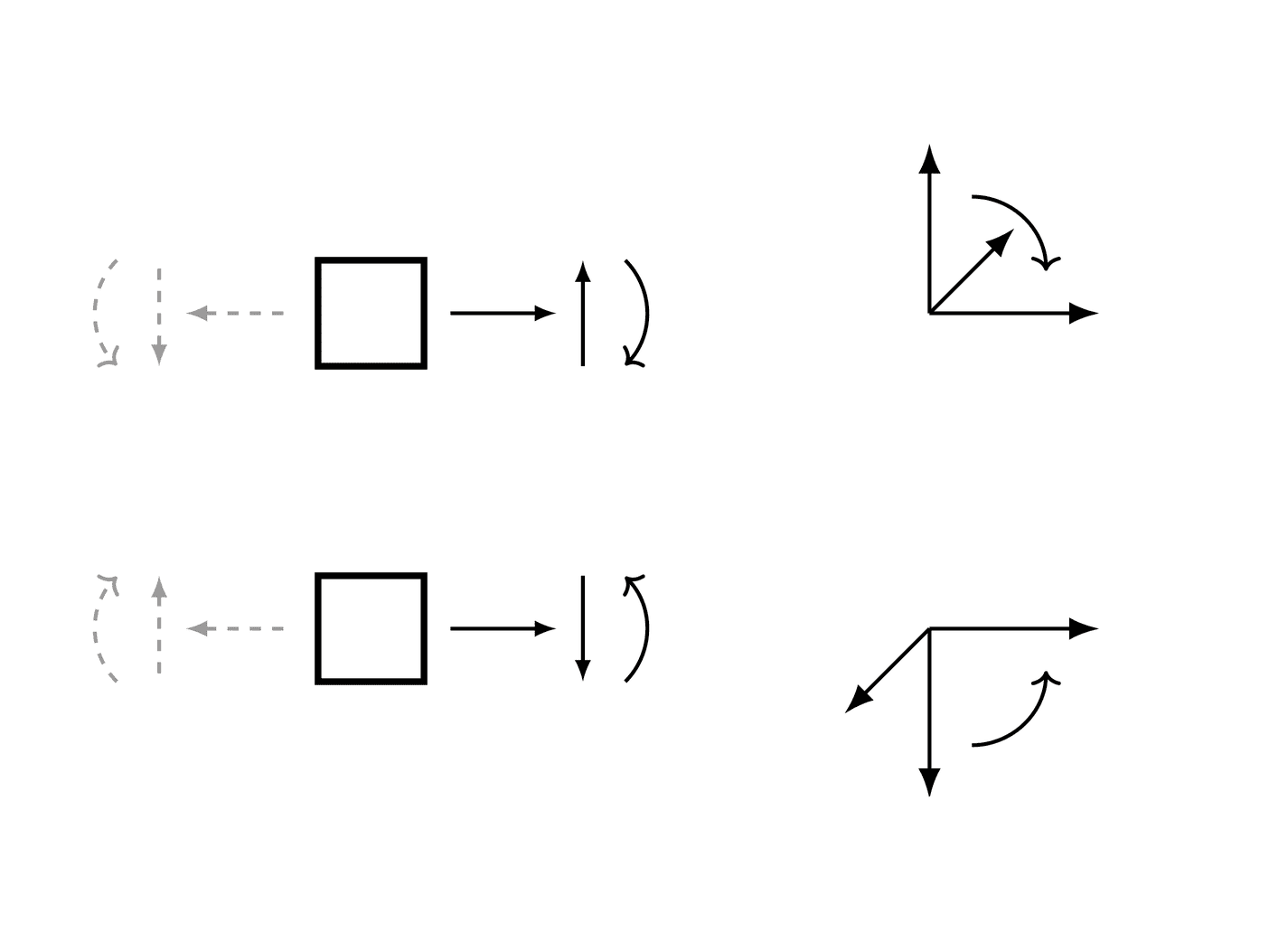
在解决梁弯曲问题时,必须使用一致的符号约定;结果将自动遵循所选的符号约定。然而,所选的符号约定必须遵守以下规则:在梁轴的正侧(相对于当前截面),产生正剪力的载荷会产生负弯矩,如下所示(弯曲箭头表示正弯矩和旋转):
- 属性:
applied_loads返回施加在梁对象上的所有载荷的列表。
area梁的横截面积。
- bc_bending_moment
- bc_deflection
- bc_shear_force
- bc_slope
boundary_conditions返回应用于梁的边界条件字典。
cross_section梁的横截面
deflection_jumps返回滑动铰链中的偏转跳跃,以字典形式表示。
elastic_modulus梁的杨氏模量。
ild_deflection_jumps返回 I.L.D.
ild_moment返回 I.L.D.
ild_reactions返回 I.L.D.
ild_rotation_jumps返回 I.L.D.
ild_shear返回 I.L.D.
length梁的长度。
load返回一个表示梁对象载荷分布曲线的奇异函数表达式。
reaction_loads返回一个字典中的反作用力。
rotation_jumps返回旋转铰链中旋转跳跃的值,以字典形式。
second_moment梁的惯性矩。
variable一个可以沿梁的长度用作变量的符号,同时表示荷载分布、剪力曲线、弯矩、斜率曲线和挠度曲线。
方法
apply_load(value, start, order[, end])此方法将给定到特定梁对象的载荷相加。
apply_rotation_hinge(loc)此方法在梁的单个位置应用旋转铰链。
apply_sliding_hinge(loc)此方法在梁的单一位置应用滑动铰链。
apply_support(loc[, type])此方法对特定梁对象施加支撑,并返回未知反作用力的符号。
返回一个表示梁对象弯矩曲线的奇异函数表达式。
返回一个表示梁对象的弹性曲线或偏转的奇异函数表达式。
draw([pictorial])返回一个表示梁的梁图的绘图对象。
join(beam[, via])此方法将两个梁连接起来,形成一个新的复合梁系统。
返回 Beam 对象中的最大剪力及其坐标。
返回梁对象中最大挠度的点及其对应的挠度值。
返回 Beam 对象中的最大剪力及其坐标。
plot_bending_moment([subs])返回 Beam 对象中存在的弯矩图。
plot_deflection([subs])返回一个用于表示 Beam 对象挠度曲线的图表。
plot_ild_moment([subs])绘制在移动荷载作用下的弯矩影响线图。
plot_ild_reactions([subs])绘制在移动载荷作用下的反力影响线图。
plot_ild_shear([subs])绘制在移动荷载作用下的剪力影响线图。
plot_loading_results([subs])返回梁对象的剪力、弯矩、斜率和挠度的子图。
plot_shear_force([subs])返回一个显示梁对象中存在的剪力的图。
plot_shear_stress([subs])返回梁对象中存在的剪应力图。
plot_slope([subs])返回 Beam 对象的挠度曲线斜率的图。
返回一组弯矩为零的点,并且这些点是梁对象的弯矩曲线从负变正或从正变负的转折点。
remove_load(value, start, order[, end])此方法移除梁对象上的特定载荷。
返回一个表示 Beam 对象剪力曲线的 Singularity Function 表达式。
返回表示 Beam 对象剪应力曲线的表达式。
slope()返回一个表示梁对象弹性曲线斜率的奇异函数表达式。
solve_for_ild_moment(distance, value, *reactions)确定在移动载荷作用下,指定点处的弯矩影响线图方程。
solve_for_ild_reactions(value, *reactions)确定在移动载荷作用下的反力影响线图方程。
solve_for_ild_shear(distance, value, *reactions)确定在移动荷载作用下,指定点的剪力影响线图方程。
solve_for_reaction_loads(*reactions)求解反作用力。
示例
有一根长度为4米的梁。从梁的一半到末端施加了一个6 N/m的恒定分布载荷。梁下方有两个简支,一个在梁的起始点,另一个在梁的末端。梁末端的挠度受到限制。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols, Piecewise >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b = Beam(4, E, I) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(6, 2, 0) >>> b.apply_load(R2, 4, -1) >>> b.bc_deflection = [(0, 0), (4, 0)] >>> b.boundary_conditions {'bending_moment': [], 'deflection': [(0, 0), (4, 0)], 'shear_force': [], 'slope': []} >>> b.load R1*SingularityFunction(x, 0, -1) + R2*SingularityFunction(x, 4, -1) + 6*SingularityFunction(x, 2, 0) >>> b.solve_for_reaction_loads(R1, R2) >>> b.load -3*SingularityFunction(x, 0, -1) + 6*SingularityFunction(x, 2, 0) - 9*SingularityFunction(x, 4, -1) >>> b.shear_force() 3*SingularityFunction(x, 0, 0) - 6*SingularityFunction(x, 2, 1) + 9*SingularityFunction(x, 4, 0) >>> b.bending_moment() 3*SingularityFunction(x, 0, 1) - 3*SingularityFunction(x, 2, 2) + 9*SingularityFunction(x, 4, 1) >>> b.slope() (-3*SingularityFunction(x, 0, 2)/2 + SingularityFunction(x, 2, 3) - 9*SingularityFunction(x, 4, 2)/2 + 7)/(E*I) >>> b.deflection() (7*x - SingularityFunction(x, 0, 3)/2 + SingularityFunction(x, 2, 4)/4 - 3*SingularityFunction(x, 4, 3)/2)/(E*I) >>> b.deflection().rewrite(Piecewise) (7*x - Piecewise((x**3, x >= 0), (0, True))/2 - 3*Piecewise(((x - 4)**3, x >= 4), (0, True))/2 + Piecewise(((x - 2)**4, x >= 2), (0, True))/4)/(E*I)
计算长度为 L 的完全符号化梁的支座反力。梁下方有两个简单支座,一个在梁的起始点,另一个在梁的终点。梁在终点的挠度受到限制。梁的载荷为:
在 L/4 处施加的向下点载荷 P1
在 L/8 处施加的向上点载荷 P2
在 L/2 处施加的逆时针力矩 M1
在 3*L/4 处施加的顺时针力矩 M2
一个分布式常量载荷 q1,向下施加,从 L/2 到 3*L/4。
一个分布式常数载荷 q2,向上施加,从 3*L/4 到 L
符号负载不需要任何假设。然而,定义一个正的长度将有助于算法计算解决方案。
>>> E, I = symbols('E, I') >>> L = symbols("L", positive=True) >>> P1, P2, M1, M2, q1, q2 = symbols("P1, P2, M1, M2, q1, q2") >>> R1, R2 = symbols('R1, R2') >>> b = Beam(L, E, I) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, L, -1) >>> b.apply_load(P1, L/4, -1) >>> b.apply_load(-P2, L/8, -1) >>> b.apply_load(M1, L/2, -2) >>> b.apply_load(-M2, 3*L/4, -2) >>> b.apply_load(q1, L/2, 0, 3*L/4) >>> b.apply_load(-q2, 3*L/4, 0, L) >>> b.bc_deflection = [(0, 0), (L, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> print(b.reaction_loads[R1]) (-3*L**2*q1 + L**2*q2 - 24*L*P1 + 28*L*P2 - 32*M1 + 32*M2)/(32*L) >>> print(b.reaction_loads[R2]) (-5*L**2*q1 + 7*L**2*q2 - 8*L*P1 + 4*L*P2 + 32*M1 - 32*M2)/(32*L)
- property applied_loads¶
返回施加在梁对象上的所有载荷的列表。列表中的每个载荷都是一个形式为 (值, 起点, 阶数, 终点) 的元组。
示例
有一根长度为4米的梁。在梁的起始点顺时针方向施加了一个大小为3 Nm的力矩。在距起始点2米处,从梁的顶部施加了一个大小为4 N的点载荷。在同一位置施加了一个大小为5 N的点载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(4, E, I) >>> b.apply_load(-3, 0, -2) >>> b.apply_load(4, 2, -1) >>> b.apply_load(5, 2, -1) >>> b.load -3*SingularityFunction(x, 0, -2) + 9*SingularityFunction(x, 2, -1) >>> b.applied_loads [(-3, 0, -2, None), (4, 2, -1, None), (5, 2, -1, None)]
- apply_load(value, start, order, end=None)[源代码][源代码]¶
此方法将给定到特定梁对象的载荷相加。
- 参数:
- 值Sympifyable
插入的值应具有单位 [力/(距离**(n+1))],其中 n 是施加载荷的阶数。施加载荷的单位:
对于力矩,单位 = kN*m
对于点载荷,单位 = kN
对于恒定分布载荷,单位 = kN/m
对于坡道载荷,单位 = kN/m/m
对于抛物线斜坡载荷,单位 = kN/m/m/m
… 等等。
- 开始Sympifyable
施加载荷的起始点。对于点矩和点力,这是施加的位置。
- 顺序整数
施加载荷的顺序。
对于时刻,顺序 = -2
对于点载荷,顺序 =-1
对于恒定分布载荷,阶数 = 0
对于斜坡载荷,顺序 = 1
对于抛物线斜坡载荷,阶数 = 2
… 等等。
- 结束可符号化的,可选的
如果载荷在梁的长度内有终点,可以使用一个可选参数。
示例
有一根长度为4米的梁。在梁的起始点顺时针方向施加了一个大小为3 Nm的力矩。在距起始点2米处的梁顶部施加了一个大小为4 N的点载荷,并且在距起始点2米到3米之间的梁下方施加了一个大小为2 N/m的抛物线斜坡载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(4, E, I) >>> b.apply_load(-3, 0, -2) >>> b.apply_load(4, 2, -1) >>> b.apply_load(-2, 2, 2, end=3) >>> b.load -3*SingularityFunction(x, 0, -2) + 4*SingularityFunction(x, 2, -1) - 2*SingularityFunction(x, 2, 2) + 2*SingularityFunction(x, 3, 0) + 4*SingularityFunction(x, 3, 1) + 2*SingularityFunction(x, 3, 2)
- apply_rotation_hinge(loc)[源代码][源代码]¶
此方法在梁的单个位置应用旋转铰链。
- 参数:
- locSympifyable
铰链应用点的位置。
- 返回:
- 符号
未知旋转跳跃乘以弹性模量和二次矩作为一个符号。
示例
有一根长度为15米的梁。销支座分别放置在0米和10米处。末端有一个固定支座。结构中有两个旋转铰链,一个在5米处,另一个在10米处。在5米处的铰链上施加了一个大小为10 kN的点载荷。从10米到末端,结构上施加了一个5 kN的分布载荷。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import Symbol >>> E = Symbol('E') >>> I = Symbol('I') >>> b = Beam(15, E, I) >>> r0 = b.apply_support(0, type='pin') >>> r10 = b.apply_support(10, type='pin') >>> r15, m15 = b.apply_support(15, type='fixed') >>> p5 = b.apply_rotation_hinge(5) >>> p12 = b.apply_rotation_hinge(12) >>> b.apply_load(-10, 5, -1) >>> b.apply_load(-5, 10, 0, 15) >>> b.solve_for_reaction_loads(r0, r10, r15, m15) >>> b.reaction_loads {M_15: -75/2, R_0: 0, R_10: 40, R_15: -5} >>> b.rotation_jumps {P_12: -1875/(16*E*I), P_5: 9625/(24*E*I)} >>> b.rotation_jumps[p12] -1875/(16*E*I) >>> b.bending_moment() -9625*SingularityFunction(x, 5, -1)/24 + 10*SingularityFunction(x, 5, 1) - 40*SingularityFunction(x, 10, 1) + 5*SingularityFunction(x, 10, 2)/2 + 1875*SingularityFunction(x, 12, -1)/16 + 75*SingularityFunction(x, 15, 0)/2 + 5*SingularityFunction(x, 15, 1) - 5*SingularityFunction(x, 15, 2)/2
- apply_sliding_hinge(loc)[源代码][源代码]¶
此方法在梁的单一位置应用滑动铰链。
- 参数:
- locSympifyable
铰链应用点的位置。
- 返回:
- 符号
未知挠度跳跃乘以弹性模量和二次矩作为符号。
示例
有一根长度为13米的梁。在起点处有一个固定支撑。在末端有一个销支撑。在8米的位置有一个滑动铰链。在5米处的铰链上施加了一个大小为10 kN的点载荷。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> b = Beam(13, 20, 20) >>> r0, m0 = b.apply_support(0, type="fixed") >>> s8 = b.apply_sliding_hinge(8) >>> r13 = b.apply_support(13, type="pin") >>> b.apply_load(-10, 5, -1) >>> b.solve_for_reaction_loads(r0, m0, r13) >>> b.reaction_loads {M_0: -50, R_0: 10, R_13: 0} >>> b.deflection_jumps {W_8: 85/24} >>> b.deflection_jumps[s8] 85/24 >>> b.bending_moment() 50*SingularityFunction(x, 0, 0) - 10*SingularityFunction(x, 0, 1) + 10*SingularityFunction(x, 5, 1) - 4250*SingularityFunction(x, 8, -2)/3 >>> b.deflection() -SingularityFunction(x, 0, 2)/16 + SingularityFunction(x, 0, 3)/240 - SingularityFunction(x, 5, 3)/240 + 85*SingularityFunction(x, 8, 0)/24
- apply_support(loc, type='fixed')[源代码][源代码]¶
此方法对特定梁对象施加支撑,并返回未知反作用力的符号。
- 参数:
- locSympifyable
施加支撑点的位置。
- 类型字符串
确定应用的梁支撑类型。要应用支撑结构,请选择以下类型: - 零自由度,type = “fixed” - 一自由度,type = “pin” - 二自由度,type = “roller”
- 返回:
- 符号或符号的元组
未知的反作用力载荷作为符号。 - 如果类型为“pin”或“roller”,则为 Symbol(reaction_force) - 如果类型为“fixed”,则为 Symbol(reaction_force), Symbol(reaction_moment)
示例
有一根长度为20米的梁。在梁的末端顺时针方向施加了一个大小为100 Nm的力矩。在距离梁顶端10米处施加了一个大小为8 N的点载荷。梁的起点有一个固定支撑,末端有一个滚轮。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(20, E, I) >>> p0, m0 = b.apply_support(0, 'fixed') >>> p1 = b.apply_support(20, 'roller') >>> b.apply_load(-8, 10, -1) >>> b.apply_load(100, 20, -2) >>> b.solve_for_reaction_loads(p0, m0, p1) >>> b.reaction_loads {M_0: 20, R_0: -2, R_20: 10} >>> b.reaction_loads[p0] -2 >>> b.load 20*SingularityFunction(x, 0, -2) - 2*SingularityFunction(x, 0, -1) - 8*SingularityFunction(x, 10, -1) + 100*SingularityFunction(x, 20, -2) + 10*SingularityFunction(x, 20, -1)
- property area¶
梁的横截面积。
- bending_moment()[源代码][源代码]¶
返回一个表示梁对象弯矩曲线的奇异函数表达式。
示例
有一根长度为30米的梁。在梁的末端施加了一个顺时针方向的120 Nm的力矩。在梁的起始点从顶部施加了一个8 N的点载荷。梁下方有两个简单的支撑。一个在末端,另一个在距离起点10米处。两个支撑点的挠度都被限制。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b = Beam(30, E, I) >>> b.apply_load(-8, 0, -1) >>> b.apply_load(R1, 10, -1) >>> b.apply_load(R2, 30, -1) >>> b.apply_load(120, 30, -2) >>> b.bc_deflection = [(10, 0), (30, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.bending_moment() 8*SingularityFunction(x, 0, 1) - 6*SingularityFunction(x, 10, 1) - 120*SingularityFunction(x, 30, 0) - 2*SingularityFunction(x, 30, 1)
- property boundary_conditions¶
返回一个应用于梁的边界条件字典。该字典有三个关键词,分别是 moment、slope 和 deflection。每个关键词的值是一个元组列表,其中每个元组包含边界条件的位置和值,格式为 (位置, 值)。
示例
有一根长度为4米的梁。在0处的弯矩应为4,在4处应为0。梁在0处的斜率应为1。在0处的挠度应为2。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(4, E, I) >>> b.bc_deflection = [(0, 2)] >>> b.bc_slope = [(0, 1)] >>> b.boundary_conditions {'bending_moment': [], 'deflection': [(0, 2)], 'shear_force': [], 'slope': [(0, 1)]}
在这里,梁的偏转应在
0处为2。同样,梁的斜率应在0处为1。
- property cross_section¶
梁的横截面
- deflection()[源代码][源代码]¶
返回一个表示梁对象的弹性曲线或偏转的奇异函数表达式。
示例
有一根长度为30米的梁。在梁的末端施加了一个顺时针方向的120 Nm的力矩。在梁的起始点从顶部施加了一个8 N的点载荷。梁下方有两个简单的支撑。一个在末端,另一个在距离起点10米处。两个支撑点的挠度都被限制。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b = Beam(30, E, I) >>> b.apply_load(-8, 0, -1) >>> b.apply_load(R1, 10, -1) >>> b.apply_load(R2, 30, -1) >>> b.apply_load(120, 30, -2) >>> b.bc_deflection = [(10, 0), (30, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.deflection() (4000*x/3 - 4*SingularityFunction(x, 0, 3)/3 + SingularityFunction(x, 10, 3) + 60*SingularityFunction(x, 30, 2) + SingularityFunction(x, 30, 3)/3 - 12000)/(E*I)
- property deflection_jumps¶
返回滑动铰链中的偏转跳跃,以字典形式表示。偏转跳跃是滑动铰链中的偏转(以米为单位)。这可以看作是偏转图中的跳跃。
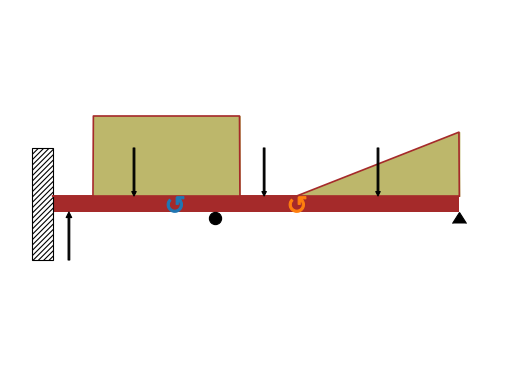
- draw(pictorial=True)[源代码][源代码]¶
返回一个表示梁的梁图的绘图对象。特别是,该图可能包括:
光束。
垂直的黑色箭头表示点载荷和支持反作用力(如果它们是通过
apply_load方法添加的)。圆形箭头代表力矩。
阴影区域代表分布载荷。
支持,如果
apply_support已被执行。如果一个组合梁是通过
join方法创建的并且指定了一个铰链,它将显示为一个白色圆盘。
该图显示了梁上侧的正载荷和下侧的负载荷。如果两个或多个分布载荷在同一方向上作用于同一区域,该函数将把它们相加。
备注
用户在输入载荷值时必须小心。绘图函数假设了一个用于绘制载荷的符号约定。给定一个右手坐标系,其中XYZ坐标,梁的长度假设沿正X轴方向。绘图函数将正载荷(n>-2)识别为沿负Y方向作用的载荷,并将正弯矩识别为沿正Z方向作用的弯矩。
- 参数:
- pictorial: Boolean (默认=True)
设置
pictorial=True将简单地创建一个梁图的图示(缩放)视图。另一方面,pictorial=False将创建一个在图上具有精确尺寸的梁图。
示例
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> P1, P2, M = symbols('P1, P2, M') >>> E, I = symbols('E, I') >>> b = Beam(50, 20, 30) >>> b.apply_load(-10, 2, -1) >>> b.apply_load(15, 26, -1) >>> b.apply_load(P1, 10, -1) >>> b.apply_load(-P2, 40, -1) >>> b.apply_load(90, 5, 0, 23) >>> b.apply_load(10, 30, 1, 50) >>> b.apply_load(M, 15, -2) >>> b.apply_load(-M, 30, -2) >>> p50 = b.apply_support(50, "pin") >>> p0, m0 = b.apply_support(0, "fixed") >>> p20 = b.apply_support(20, "roller") >>> p = b.draw() >>> p Plot object containing: [0]: cartesian line: 25*SingularityFunction(x, 5, 0) - 25*SingularityFunction(x, 23, 0) + SingularityFunction(x, 30, 1) - 20*SingularityFunction(x, 50, 0) - SingularityFunction(x, 50, 1) + 5 for x over (0.0, 50.0) [1]: cartesian line: 5 for x over (0.0, 50.0) ... >>> p.show()
- property elastic_modulus¶
梁的杨氏模量。
- property ild_deflection_jumps¶
返回滑动铰链中的 I.L.D. 偏转跳变,以字典形式表示。偏转跳变是滑动铰链中的偏转(以米为单位)。这可以看作是偏转图中的跳变。
- property ild_moment¶
返回 I.L.D. 力矩方程。
- property ild_reactions¶
返回字典中的 I.L.D. 反作用力。
- property ild_rotation_jumps¶
返回字典中的 I.L.D. 旋转跳跃在旋转铰链中。旋转跳跃是旋转铰链中的旋转(以弧度为单位)。这可以看作是斜率图中的跳跃。
- property ild_shear¶
返回 I.L.D. 剪切方程。
- join(beam, via='fixed')[源代码][源代码]¶
此方法将两个梁连接起来,形成一个新的复合梁系统。传递的 Beam 类实例被附加到调用对象的右端。此方法可用于形成具有不连续弹性模量或惯性矩值的梁。
- 参数:
- 光束Beam 类对象
与调用对象右侧连接的 Beam 对象。
- 通过字符串
说明两个Beam对象的连接方式 - 对于轴向固定的Beam,via=”fixed” - 对于通过旋转铰链连接的Beam,via=”hinge”
示例
有一根长度为4米的悬臂梁。前2米的惯性矩为 \(1.5*I\),其余部分的惯性矩为 \(I\)。在其自由端顶部施加了一个大小为4 N的点载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b1 = Beam(2, E, 1.5*I) >>> b2 = Beam(2, E, I) >>> b = b1.join(b2, "fixed") >>> b.apply_load(20, 4, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 0, -2) >>> b.bc_slope = [(0, 0)] >>> b.bc_deflection = [(0, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.load 80*SingularityFunction(x, 0, -2) - 20*SingularityFunction(x, 0, -1) + 20*SingularityFunction(x, 4, -1) >>> b.slope() (-((-80*SingularityFunction(x, 0, 1) + 10*SingularityFunction(x, 0, 2) - 10*SingularityFunction(x, 4, 2))/I + 120/I)/E + 80.0/(E*I))*SingularityFunction(x, 2, 0) - 0.666666666666667*(-80*SingularityFunction(x, 0, 1) + 10*SingularityFunction(x, 0, 2) - 10*SingularityFunction(x, 4, 2))*SingularityFunction(x, 0, 0)/(E*I) + 0.666666666666667*(-80*SingularityFunction(x, 0, 1) + 10*SingularityFunction(x, 0, 2) - 10*SingularityFunction(x, 4, 2))*SingularityFunction(x, 2, 0)/(E*I)
- property length¶
梁的长度。
- property load¶
返回一个表示梁对象载荷分布曲线的奇异函数表达式。
示例
有一根长度为4米的梁。在梁的起始点施加了一个大小为3 Nm的顺时针方向的力矩。在距起始点2米处的梁顶部施加了一个大小为4 N的点载荷,并且在距起始点3米处的梁下方施加了一个大小为2 N/m的抛物线斜坡载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(4, E, I) >>> b.apply_load(-3, 0, -2) >>> b.apply_load(4, 2, -1) >>> b.apply_load(-2, 3, 2) >>> b.load -3*SingularityFunction(x, 0, -2) + 4*SingularityFunction(x, 2, -1) - 2*SingularityFunction(x, 3, 2)
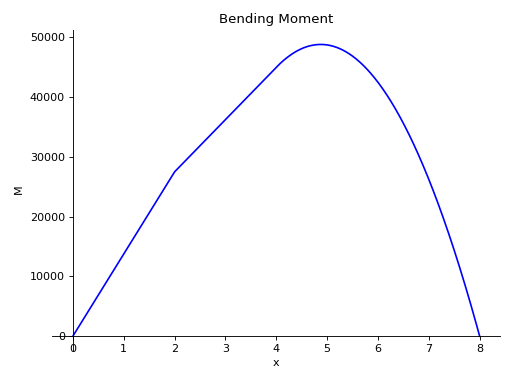
- plot_bending_moment(subs=None)[源代码][源代码]¶
返回 Beam 对象中存在的弯矩图。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为8米的梁。从梁的一半到末端施加了一个恒定的分布载荷,大小为10 KN/m。梁下方有两个简单的支撑,一个在梁的起始点,另一个在梁的末端。在梁的顶部,距离起始点4米处还施加了一个大小为5 KN的点载荷。取E = 200 GPa,I = 400*(10**-6) 米**4。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> R1, R2 = symbols('R1, R2') >>> b = Beam(8, 200*(10**9), 400*(10**-6)) >>> b.apply_load(5000, 2, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 8, -1) >>> b.apply_load(10000, 4, 0, end=8) >>> b.bc_deflection = [(0, 0), (8, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.plot_bending_moment() Plot object containing: [0]: cartesian line: 13750*SingularityFunction(x, 0, 1) - 5000*SingularityFunction(x, 2, 1) - 5000*SingularityFunction(x, 4, 2) + 31250*SingularityFunction(x, 8, 1) + 5000*SingularityFunction(x, 8, 2) for x over (0.0, 8.0)
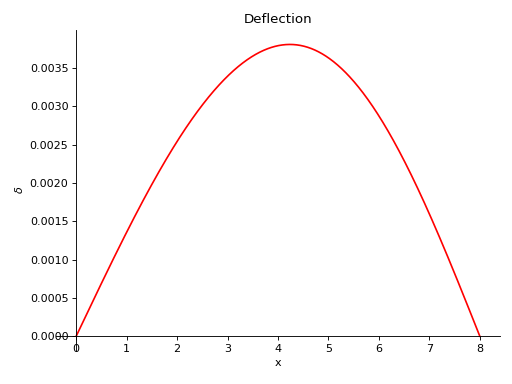
- plot_deflection(subs=None)[源代码][源代码]¶
返回一个用于表示 Beam 对象挠度曲线的图表。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为8米的梁。从梁的一半到末端施加了一个恒定的分布载荷,大小为10 KN/m。梁下方有两个简单的支撑,一个在梁的起始点,另一个在梁的末端。在梁的顶部,距离起始点4米处还施加了一个大小为5 KN的点载荷。取E = 200 GPa,I = 400*(10**-6) 米**4。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> R1, R2 = symbols('R1, R2') >>> b = Beam(8, 200*(10**9), 400*(10**-6)) >>> b.apply_load(5000, 2, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 8, -1) >>> b.apply_load(10000, 4, 0, end=8) >>> b.bc_deflection = [(0, 0), (8, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.plot_deflection() Plot object containing: [0]: cartesian line: 0.00138541666666667*x - 2.86458333333333e-5*SingularityFunction(x, 0, 3) + 1.04166666666667e-5*SingularityFunction(x, 2, 3) + 5.20833333333333e-6*SingularityFunction(x, 4, 4) - 6.51041666666667e-5*SingularityFunction(x, 8, 3) - 5.20833333333333e-6*SingularityFunction(x, 8, 4) for x over (0.0, 8.0)
- plot_ild_moment(subs=None)[源代码][源代码]¶
绘制在移动荷载作用下的弯矩影响线图。此函数应在调用 solve_for_ild_moment() 之后调用。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为12米的梁。梁下方有两个简单支撑,一个在起点,另一个在距离起点8米处。绘制在距离起点4米处,在1kN移动荷载作用下的弯矩影响线(I.L.D.)。
使用向下力为正的符号约定。
>>> from sympy import symbols >>> from sympy.physics.continuum_mechanics.beam import Beam >>> E, I = symbols('E, I') >>> R_0, R_8 = symbols('R_0, R_8') >>> b = Beam(12, E, I) >>> p0 = b.apply_support(0, 'roller') >>> p8 = b.apply_support(8, 'roller') >>> b.solve_for_ild_reactions(1, R_0, R_8) >>> b.solve_for_ild_moment(4, 1, R_0, R_8) >>> b.ild_moment -(4*SingularityFunction(a, 0, 0) - SingularityFunction(a, 0, 1) + SingularityFunction(a, 4, 1))*SingularityFunction(a, 4, 0) - SingularityFunction(a, 0, 1)/2 + SingularityFunction(a, 4, 1) - 2*SingularityFunction(a, 12, 0) - SingularityFunction(a, 12, 1)/2 >>> b.plot_ild_moment() Plot object containing: [0]: cartesian line: -(4*SingularityFunction(a, 0, 0) - SingularityFunction(a, 0, 1) + SingularityFunction(a, 4, 1))*SingularityFunction(a, 4, 0) - SingularityFunction(a, 0, 1)/2 + SingularityFunction(a, 4, 1) - 2*SingularityFunction(a, 12, 0) - SingularityFunction(a, 12, 1)/2 for a over (0.0, 12.0)
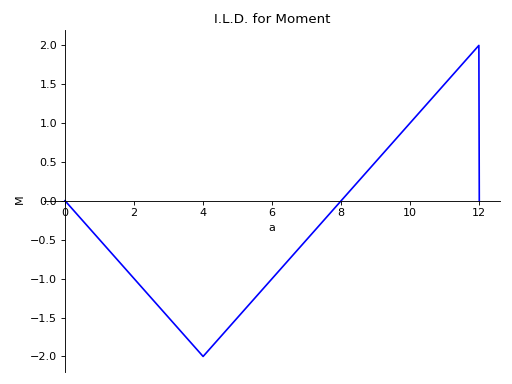
- plot_ild_reactions(subs=None)[源代码][源代码]¶
绘制在移动载荷作用下的反力影响线图。此函数应在调用 solve_for_ild_reactions() 之后调用。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为10米的梁。在距离起点4米处,从梁的顶部施加了一个大小为5kN的点载荷。梁下方有两个简单的支撑,分别位于起点和距离起点7米处。绘制在大小为1kN的移动载荷作用下,两个支撑点处反应的I.L.D.方程。
使用向下力为正的符号约定。
>>> from sympy import symbols >>> from sympy.physics.continuum_mechanics.beam import Beam >>> E, I = symbols('E, I') >>> R_0, R_7 = symbols('R_0, R_7') >>> b = Beam(10, E, I) >>> p0 = b.apply_support(0, 'roller') >>> p7 = b.apply_support(7, 'roller') >>> b.apply_load(5,4,-1) >>> b.solve_for_ild_reactions(1,R_0,R_7) >>> b.ild_reactions {R_0: -SingularityFunction(a, 0, 0) + SingularityFunction(a, 0, 1)/7 - 3*SingularityFunction(a, 10, 0)/7 - SingularityFunction(a, 10, 1)/7 - 15/7, R_7: -SingularityFunction(a, 0, 1)/7 + 10*SingularityFunction(a, 10, 0)/7 + SingularityFunction(a, 10, 1)/7 - 20/7} >>> b.plot_ild_reactions() PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: -SingularityFunction(a, 0, 0) + SingularityFunction(a, 0, 1)/7 - 3*SingularityFunction(a, 10, 0)/7 - SingularityFunction(a, 10, 1)/7 - 15/7 for a over (0.0, 10.0) Plot[1]:Plot object containing: [0]: cartesian line: -SingularityFunction(a, 0, 1)/7 + 10*SingularityFunction(a, 10, 0)/7 + SingularityFunction(a, 10, 1)/7 - 20/7 for a over (0.0, 10.0)
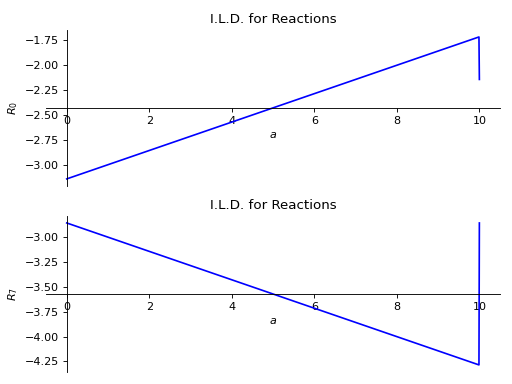
- plot_ild_shear(subs=None)[源代码][源代码]¶
绘制在移动荷载作用下的剪力影响线图。此函数应在调用 solve_for_ild_shear() 之后调用。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为12米的梁。梁下方有两个简支点,一个在起点,另一个在距离起点8米处。绘制在距离起点4米处的剪力影响线(I.L.D.),考虑一个大小为1kN的移动荷载的影响。
使用向下力为正的符号约定。
>>> from sympy import symbols >>> from sympy.physics.continuum_mechanics.beam import Beam >>> E, I = symbols('E, I') >>> R_0, R_8 = symbols('R_0, R_8') >>> b = Beam(12, E, I) >>> p0 = b.apply_support(0, 'roller') >>> p8 = b.apply_support(8, 'roller') >>> b.solve_for_ild_reactions(1, R_0, R_8) >>> b.solve_for_ild_shear(4, 1, R_0, R_8) >>> b.ild_shear -(-SingularityFunction(a, 0, 0) + SingularityFunction(a, 12, 0) + 2)*SingularityFunction(a, 4, 0) - SingularityFunction(-a, 0, 0) - SingularityFunction(a, 0, 0) + SingularityFunction(a, 0, 1)/8 + SingularityFunction(a, 12, 0)/2 - SingularityFunction(a, 12, 1)/8 + 1 >>> b.plot_ild_shear() Plot object containing: [0]: cartesian line: -(-SingularityFunction(a, 0, 0) + SingularityFunction(a, 12, 0) + 2)*SingularityFunction(a, 4, 0) - SingularityFunction(-a, 0, 0) - SingularityFunction(a, 0, 0) + SingularityFunction(a, 0, 1)/8 + SingularityFunction(a, 12, 0)/2 - SingularityFunction(a, 12, 1)/8 + 1 for a over (0.0, 12.0)
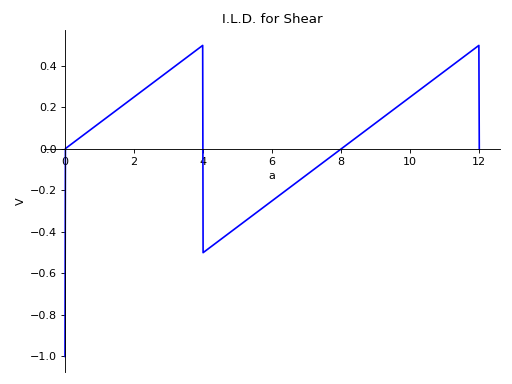
- plot_loading_results(subs=None)[源代码][源代码]¶
返回梁对象的剪力、弯矩、斜率和挠度的子图。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为8米的梁。从梁的一半到末端施加了一个恒定的分布载荷,大小为10 KN/m。梁下方有两个简单的支撑,一个在梁的起始点,另一个在梁的末端。在梁的顶部,距离起始点4米处还施加了一个大小为5 KN的点载荷。取E = 200 GPa,I = 400*(10**-6) 米**4。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> R1, R2 = symbols('R1, R2') >>> b = Beam(8, 200*(10**9), 400*(10**-6)) >>> b.apply_load(5000, 2, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 8, -1) >>> b.apply_load(10000, 4, 0, end=8) >>> b.bc_deflection = [(0, 0), (8, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> axes = b.plot_loading_results()
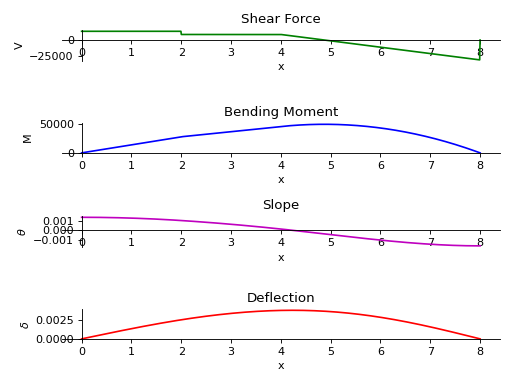
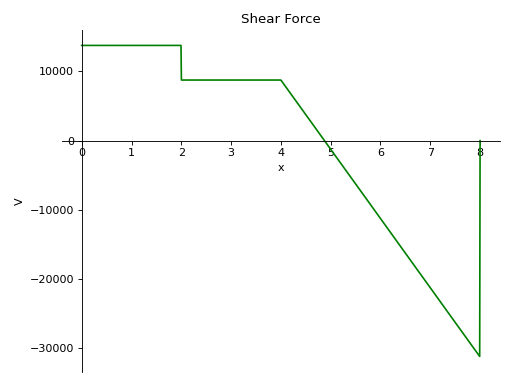
- plot_shear_force(subs=None)[源代码][源代码]¶
返回一个显示梁对象中存在的剪力的图。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为8米的梁。从梁的一半到末端施加了一个恒定的分布载荷,大小为10 KN/m。梁下方有两个简单的支撑,一个在梁的起始点,另一个在梁的末端。在梁的顶部,距离起始点4米处还施加了一个大小为5 KN的点载荷。取E = 200 GPa,I = 400*(10**-6) 米**4。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> R1, R2 = symbols('R1, R2') >>> b = Beam(8, 200*(10**9), 400*(10**-6)) >>> b.apply_load(5000, 2, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 8, -1) >>> b.apply_load(10000, 4, 0, end=8) >>> b.bc_deflection = [(0, 0), (8, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.plot_shear_force() Plot object containing: [0]: cartesian line: 13750*SingularityFunction(x, 0, 0) - 5000*SingularityFunction(x, 2, 0) - 10000*SingularityFunction(x, 4, 1) + 31250*SingularityFunction(x, 8, 0) + 10000*SingularityFunction(x, 8, 1) for x over (0.0, 8.0)
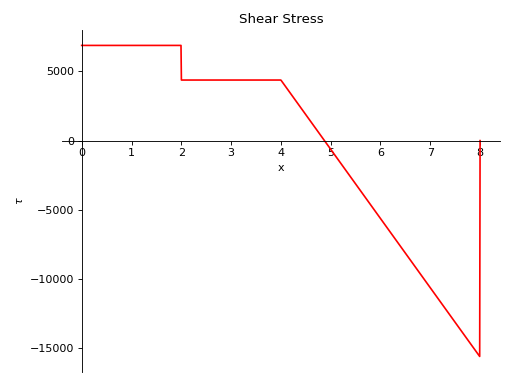
- plot_shear_stress(subs=None)[源代码][源代码]¶
返回梁对象中存在的剪应力图。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为8米、横截面积为2平方米的梁。从梁的一半到末端施加了一个10 KN/m的恒定分布载荷。梁下方有两个简单的支撑,一个在起点,另一个在梁的终点。在距起点4米处,从梁的顶部施加了一个大小为5 KN的点载荷。取E = 200 GPa,I = 400*(10**-6) 米**4。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> R1, R2 = symbols('R1, R2') >>> b = Beam(8, 200*(10**9), 400*(10**-6), 2) >>> b.apply_load(5000, 2, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 8, -1) >>> b.apply_load(10000, 4, 0, end=8) >>> b.bc_deflection = [(0, 0), (8, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.plot_shear_stress() Plot object containing: [0]: cartesian line: 6875*SingularityFunction(x, 0, 0) - 2500*SingularityFunction(x, 2, 0) - 5000*SingularityFunction(x, 4, 1) + 15625*SingularityFunction(x, 8, 0) + 5000*SingularityFunction(x, 8, 1) for x over (0.0, 8.0)
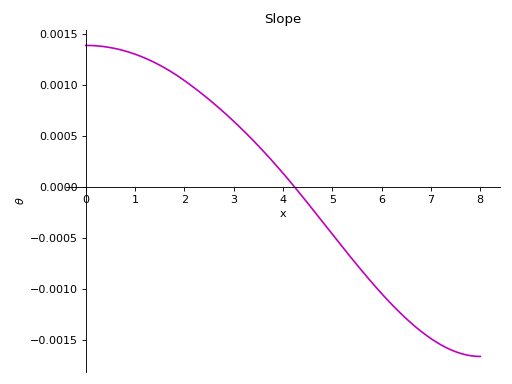
- plot_slope(subs=None)[源代码][源代码]¶
返回 Beam 对象的挠度曲线斜率的图。
- 参数:
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为8米的梁。从梁的一半到末端施加了一个恒定的分布载荷,大小为10 KN/m。梁下方有两个简单的支撑,一个在梁的起始点,另一个在梁的末端。在梁的顶部,距离起始点4米处还施加了一个大小为5 KN的点载荷。取E = 200 GPa,I = 400*(10**-6) 米**4。
使用向下力为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> R1, R2 = symbols('R1, R2') >>> b = Beam(8, 200*(10**9), 400*(10**-6)) >>> b.apply_load(5000, 2, -1) >>> b.apply_load(R1, 0, -1) >>> b.apply_load(R2, 8, -1) >>> b.apply_load(10000, 4, 0, end=8) >>> b.bc_deflection = [(0, 0), (8, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.plot_slope() Plot object containing: [0]: cartesian line: -8.59375e-5*SingularityFunction(x, 0, 2) + 3.125e-5*SingularityFunction(x, 2, 2) + 2.08333333333333e-5*SingularityFunction(x, 4, 3) - 0.0001953125*SingularityFunction(x, 8, 2) - 2.08333333333333e-5*SingularityFunction(x, 8, 3) + 0.00138541666666667 for x over (0.0, 8.0)
- point_cflexure()[源代码][源代码]¶
返回一组弯矩为零的点,并且这些点是梁对象的弯矩曲线从负变正或从正变负的转折点。
示例
这里有一个10米长的悬臂梁。梁下方有两个简单支撑。一个在起点,另一个在距离起点6米处。在距离起点2米和4米处分别施加了大小为10KN和20KN的点载荷。从距离起点6米处开始到末端,还施加了大小为3KN/m的均布载荷。使用向上力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(10, E, I) >>> b.apply_load(-4, 0, -1) >>> b.apply_load(-46, 6, -1) >>> b.apply_load(10, 2, -1) >>> b.apply_load(20, 4, -1) >>> b.apply_load(3, 6, 0) >>> b.point_cflexure() [10/3]
- property reaction_loads¶
返回一个字典中的反作用力。
- remove_load(value, start, order, end=None)[源代码][源代码]¶
此方法移除梁对象上的特定载荷。如果作为参数传递的载荷不在梁上,则返回 ValueError。
- 参数:
- 值Sympifyable
施加载荷的大小。
- 开始Sympifyable
施加载荷的起始点。对于点矩和点力,这是施加的位置。
- 顺序整数
应用载荷的顺序。 - 对于弯矩,顺序= -2 - 对于点载荷,顺序= -1 - 对于恒定分布载荷,顺序= 0 - 对于斜坡载荷,顺序= 1 - 对于抛物线斜坡载荷,顺序= 2 - … 以此类推。
- 结束可符号化的,可选的
如果载荷在梁的长度内有终点,可以使用一个可选参数。
示例
有一根长度为4米的梁。在梁的起始点施加了一个大小为3 Nm的顺时针方向的力矩。在距起始点2米处的梁顶部施加了一个大小为4 N的点载荷,并且在距起始点2米到3米之间的梁下方施加了一个大小为2 N/m的抛物线斜坡载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> b = Beam(4, E, I) >>> b.apply_load(-3, 0, -2) >>> b.apply_load(4, 2, -1) >>> b.apply_load(-2, 2, 2, end=3) >>> b.load -3*SingularityFunction(x, 0, -2) + 4*SingularityFunction(x, 2, -1) - 2*SingularityFunction(x, 2, 2) + 2*SingularityFunction(x, 3, 0) + 4*SingularityFunction(x, 3, 1) + 2*SingularityFunction(x, 3, 2) >>> b.remove_load(-2, 2, 2, end = 3) >>> b.load -3*SingularityFunction(x, 0, -2) + 4*SingularityFunction(x, 2, -1)
- property rotation_jumps¶
返回旋转铰链中旋转跳跃值的字典。旋转跳跃是旋转铰链中的旋转(以弧度为单位)。这可以看作是斜率图中的跳跃。
- property second_moment¶
梁的惯性矩。
- shear_force()[源代码][源代码]¶
返回一个表示 Beam 对象剪力曲线的 Singularity Function 表达式。
示例
有一根长度为30米的梁。在梁的末端施加了一个顺时针方向的120 Nm的力矩。在梁的起始点从顶部施加了一个8 N的点载荷。梁下方有两个简单的支撑。一个在末端,另一个在距离起点10米处。两个支撑点的挠度都被限制。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b = Beam(30, E, I) >>> b.apply_load(-8, 0, -1) >>> b.apply_load(R1, 10, -1) >>> b.apply_load(R2, 30, -1) >>> b.apply_load(120, 30, -2) >>> b.bc_deflection = [(10, 0), (30, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.shear_force() 8*SingularityFunction(x, 0, 0) - 6*SingularityFunction(x, 10, 0) - 120*SingularityFunction(x, 30, -1) - 2*SingularityFunction(x, 30, 0)
- slope()[源代码][源代码]¶
返回一个表示梁对象弹性曲线斜率的奇异函数表达式。
示例
有一根长度为30米的梁。在梁的末端施加了一个顺时针方向的120 Nm的力矩。在梁的起始点从顶部施加了一个8 N的点载荷。梁下方有两个简单的支撑。一个在末端,另一个在距离起点10米处。两个支撑点的挠度都被限制。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b = Beam(30, E, I) >>> b.apply_load(-8, 0, -1) >>> b.apply_load(R1, 10, -1) >>> b.apply_load(R2, 30, -1) >>> b.apply_load(120, 30, -2) >>> b.bc_deflection = [(10, 0), (30, 0)] >>> b.solve_for_reaction_loads(R1, R2) >>> b.slope() (-4*SingularityFunction(x, 0, 2) + 3*SingularityFunction(x, 10, 2) + 120*SingularityFunction(x, 30, 1) + SingularityFunction(x, 30, 2) + 4000/3)/(E*I)
- solve_for_ild_moment(
- distance,
- value,
- *reactions,
确定在移动载荷作用下,指定点处的弯矩影响线图方程。
- 参数:
- 距离整数
确定方程所需的点与梁起点的距离
- 值整数
移动载荷的量级
- 反应
施加在梁上的反作用力。
示例
有一根长度为12米的梁。梁下方有两个简单支座,一个在起点,另一个在距离起点8米处。计算在大小为1kN的移动载荷作用下,距离起点4米处的弯矩影响线方程。
使用向下力为正的符号约定。
>>> from sympy import symbols >>> from sympy.physics.continuum_mechanics.beam import Beam >>> E, I = symbols('E, I') >>> R_0, R_8 = symbols('R_0, R_8') >>> b = Beam(12, E, I) >>> p0 = b.apply_support(0, 'roller') >>> p8 = b.apply_support(8, 'roller') >>> b.solve_for_ild_reactions(1, R_0, R_8) >>> b.solve_for_ild_moment(4, 1, R_0, R_8) >>> b.ild_moment -(4*SingularityFunction(a, 0, 0) - SingularityFunction(a, 0, 1) + SingularityFunction(a, 4, 1))*SingularityFunction(a, 4, 0) - SingularityFunction(a, 0, 1)/2 + SingularityFunction(a, 4, 1) - 2*SingularityFunction(a, 12, 0) - SingularityFunction(a, 12, 1)/2
- solve_for_ild_reactions(value, *reactions)[源代码][源代码]¶
确定在移动载荷作用下的反力影响线图方程。
- 参数:
- 值整数
移动载荷的量级
- 反应
施加在梁上的反作用力。
示例
有一根长度为10米的梁。梁下方有两个简单支撑,一个在梁的起点,另一个在梁的终点。计算在1kN移动载荷作用下的反力影响线方程。
使用向下力为正的符号约定。
>>> from sympy import symbols >>> from sympy.physics.continuum_mechanics.beam import Beam >>> E, I = symbols('E, I') >>> R_0, R_10 = symbols('R_0, R_10') >>> b = Beam(10, E, I) >>> p0 = b.apply_support(0, 'pin') >>> p10 = b.apply_support(10, 'roller') >>> b.solve_for_ild_reactions(1,R_0,R_10) >>> b.ild_reactions {R_0: -SingularityFunction(a, 0, 0) + SingularityFunction(a, 0, 1)/10 - SingularityFunction(a, 10, 1)/10, R_10: -SingularityFunction(a, 0, 1)/10 + SingularityFunction(a, 10, 0) + SingularityFunction(a, 10, 1)/10}
- solve_for_ild_shear(
- distance,
- value,
- *reactions,
确定在移动荷载作用下,指定点的剪力影响线图方程。
- 参数:
- 距离整数
确定方程所需的点与梁起点的距离
- 值整数
移动载荷的量级
- 反应
施加在梁上的反作用力。
示例
有一根长度为12米的梁。梁下方有两个简单支撑,一个在起点,另一个在距离起点8米处。计算在1kN移动载荷作用下,距离起点4米处的剪力影响线方程。
使用向下力为正的符号约定。
>>> from sympy import symbols >>> from sympy.physics.continuum_mechanics.beam import Beam >>> E, I = symbols('E, I') >>> R_0, R_8 = symbols('R_0, R_8') >>> b = Beam(12, E, I) >>> p0 = b.apply_support(0, 'roller') >>> p8 = b.apply_support(8, 'roller') >>> b.solve_for_ild_reactions(1, R_0, R_8) >>> b.solve_for_ild_shear(4, 1, R_0, R_8) >>> b.ild_shear -(-SingularityFunction(a, 0, 0) + SingularityFunction(a, 12, 0) + 2)*SingularityFunction(a, 4, 0) - SingularityFunction(-a, 0, 0) - SingularityFunction(a, 0, 0) + SingularityFunction(a, 0, 1)/8 + SingularityFunction(a, 12, 0)/2 - SingularityFunction(a, 12, 1)/8 + 1
- solve_for_reaction_loads(*reactions)[源代码][源代码]¶
求解反作用力。
示例
有一根长度为30米的梁。在梁的末端施加了一个顺时针方向的120 Nm的力矩。在梁的起始点从顶部施加了一个8 N的点载荷。梁下方有两个简单的支撑。一个在末端,另一个在距离起点10米处。两个支撑点的挠度都被限制。
使用向上的力和顺时针力矩为正的符号约定。
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I = symbols('E, I') >>> R1, R2 = symbols('R1, R2') >>> b = Beam(30, E, I) >>> b.apply_load(-8, 0, -1) >>> b.apply_load(R1, 10, -1) # Reaction force at x = 10 >>> b.apply_load(R2, 30, -1) # Reaction force at x = 30 >>> b.apply_load(120, 30, -2) >>> b.bc_deflection = [(10, 0), (30, 0)] >>> b.load R1*SingularityFunction(x, 10, -1) + R2*SingularityFunction(x, 30, -1) - 8*SingularityFunction(x, 0, -1) + 120*SingularityFunction(x, 30, -2) >>> b.solve_for_reaction_loads(R1, R2) >>> b.reaction_loads {R1: 6, R2: 2} >>> b.load -8*SingularityFunction(x, 0, -1) + 6*SingularityFunction(x, 10, -1) + 120*SingularityFunction(x, 30, -2) + 2*SingularityFunction(x, 30, -1)
- property variable¶
一个符号,可以在梁的长度上用作变量,同时表示载荷分布、剪力曲线、弯矩、斜率曲线和挠度曲线。默认情况下,它设置为
Symbol('x'),但此属性是可变的。示例
>>> from sympy.physics.continuum_mechanics.beam import Beam >>> from sympy import symbols >>> E, I, A = symbols('E, I, A') >>> x, y, z = symbols('x, y, z') >>> b = Beam(4, E, I) >>> b.variable x >>> b.variable = y >>> b.variable y >>> b = Beam(4, E, I, A, z) >>> b.variable z
- class sympy.physics.continuum_mechanics.beam.Beam3D(
- length,
- elastic_modulus,
- shear_modulus,
- second_moment,
- area,
- variable=x,
此类处理在三维空间任意方向施加的载荷,以及沿不同轴的不等二次矩值。
备注
在解决梁弯曲问题时,必须使用一致的符号约定;结果将自动遵循所选的符号约定。此类假设任何类型的分布载荷/弯矩在整个梁跨度上施加。
- 属性:
applied_loads返回施加在梁对象上的所有载荷的列表。
area梁的横截面积。
- bc_bending_moment
- bc_deflection
- bc_shear_force
- bc_slope
boundary_conditions返回应用于梁的边界条件字典。
cross_section梁的横截面
deflection_jumps返回滑动铰链中的偏转跳跃,以字典形式表示。
elastic_modulus梁的杨氏模量。
ild_deflection_jumps返回 I.L.D.
ild_moment返回 I.L.D.
ild_reactions返回 I.L.D.
ild_rotation_jumps返回 I.L.D.
ild_shear返回 I.L.D.
length梁的长度。
load返回一个表示梁对象载荷分布曲线的奇异函数表达式。
load_vector返回一个表示载荷向量的三元素列表。
moment_load_vector返回一个三元素列表,表示梁上的力矩载荷。
reaction_loads返回一个字典中的反作用力。
rotation_jumps返回旋转铰链中旋转跳跃的值,以字典形式。
second_moment梁的惯性矩。
shear_modulus梁的杨氏模量。
variable一个可以沿梁的长度用作变量的符号,同时表示荷载分布、剪力曲线、弯矩、斜率曲线和挠度曲线。
方法
返回一个函数 x ,描述由于 x 轴上的力矩引起的梁的角偏转如何随 x 变化。
apply_load(value, start, order[, dir])此方法将力载荷添加到特定的梁对象。
apply_moment_load(value, start, order[, dir])此方法将力矩载荷加到特定的梁对象上。
apply_rotation_hinge(loc)此方法在梁的单个位置应用旋转铰链。
apply_sliding_hinge(loc)此方法在梁的单一位置应用滑动铰链。
apply_support(loc[, type])返回 Beam 对象内部存在的轴向剪切力的表达式。
返回 Beam 对象内部存在的轴向应力的表达式。
返回一个包含三个表达式的列表,这些表达式表示沿 Beam 对象所有三个轴的弯矩曲线。
返回一个三元素列表,表示沿所有三个轴的挠曲线。
draw([pictorial])返回一个表示梁的梁图的绘图对象。
join(beam[, via])此方法将两个梁连接起来,形成一个新的复合梁系统。
返回梁对象中所有方向上的最大弯矩点及其对应的弯矩值,作为一个列表。
返回梁对象中所有方向上的最大弯矩点及其对应的弯矩值,作为一个列表。
返回梁对象中所有方向上的最大挠度点及其对应的挠度值,作为一个列表。
返回梁对象中所有方向上的最大剪切力点及其对应的剪切值,作为一个列表。
plot_bending_moment([dir, subs])返回沿 Beam 对象中所有三个方向的弯矩图。
plot_deflection([dir, subs])返回一个针对 Beam 对象中所有三个方向的偏转图。
plot_ild_moment([subs])绘制在移动荷载作用下的弯矩影响线图。
plot_ild_reactions([subs])绘制在移动载荷作用下的反力影响线图。
plot_ild_shear([subs])绘制在移动荷载作用下的剪力影响线图。
plot_loading_results([dir, subs])返回指定方向上梁对象的剪力、弯矩、斜率和挠度的子图。
plot_shear_force([dir, subs])返回一个沿梁对象中所有三个方向的剪力图。
plot_shear_stress([dir, subs])返回一个沿梁对象中所有三个方向的剪应力图。
plot_slope([dir, subs])返回一个沿 Beam 对象中所有三个方向的斜率图。
point_cflexure()返回一组弯矩为零的点,并且这些点是梁对象的弯矩曲线从负变正或从正变负的转折点。
返回梁相对于质心的X轴的极惯性矩。
remove_load(value, start, order[, end])此方法移除梁对象上的特定载荷。
返回一个包含三个表达式的列表,这些表达式表示沿所有三个轴的 Beam 对象的剪力曲线。
返回一个包含三个表达式的列表,这些表达式表示沿所有三个轴的 Beam 对象的剪应力曲线。
slope()返回一个三元素列表,表示沿所有三个轴的挠曲线斜率。
solve_for_ild_moment(distance, value, *reactions)确定在移动载荷作用下,指定点处的弯矩影响线图方程。
solve_for_ild_reactions(value, *reactions)确定在移动载荷作用下的反力影响线图方程。
solve_for_ild_shear(distance, value, *reactions)确定在移动荷载作用下,指定点的剪力影响线图方程。
solve_for_reaction_loads(*reaction)求解反作用力。
求解由于在x方向(即进出梁的方向)施加的力矩引起的扭转效应导致的角偏转。
返回梁对象内部存在的扭矩表达式。
solve_slope_deflection
参考文献
示例
有一个长度为 l 米的梁。从梁的起点到终点,沿 y 轴施加了一个大小为 q 的恒定分布载荷。从梁的起点到终点,沿 z 轴还施加了一个大小为 m 的恒定分布力矩。梁的两端固定。因此,梁在两端的挠度受到限制。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols, simplify, collect, factor >>> l, E, G, I, A = symbols('l, E, G, I, A') >>> b = Beam3D(l, E, G, I, A) >>> x, q, m = symbols('x, q, m') >>> b.apply_load(q, 0, 0, dir="y") >>> b.apply_moment_load(m, 0, -1, dir="z") >>> b.shear_force() [0, -q*x, 0] >>> b.bending_moment() [0, 0, -m*x + q*x**2/2] >>> b.bc_slope = [(0, [0, 0, 0]), (l, [0, 0, 0])] >>> b.bc_deflection = [(0, [0, 0, 0]), (l, [0, 0, 0])] >>> b.solve_slope_deflection() >>> factor(b.slope()) [0, 0, x*(-l + x)*(-A*G*l**3*q + 2*A*G*l**2*q*x - 12*E*I*l*q - 72*E*I*m + 24*E*I*q*x)/(12*E*I*(A*G*l**2 + 12*E*I))] >>> dx, dy, dz = b.deflection() >>> dy = collect(simplify(dy), x) >>> dx == dz == 0 True >>> dy == (x*(12*E*I*l*(A*G*l**2*q - 2*A*G*l*m + 12*E*I*q) ... + x*(A*G*l*(3*l*(A*G*l**2*q - 2*A*G*l*m + 12*E*I*q) + x*(-2*A*G*l**2*q + 4*A*G*l*m - 24*E*I*q)) ... + A*G*(A*G*l**2 + 12*E*I)*(-2*l**2*q + 6*l*m - 4*m*x + q*x**2) ... - 12*E*I*q*(A*G*l**2 + 12*E*I)))/(24*A*E*G*I*(A*G*l**2 + 12*E*I))) True
- apply_load(value, start, order, dir='y')[源代码][源代码]¶
此方法将力载荷添加到特定的梁对象。
- 参数:
- 值Sympifyable
施加载荷的大小。
- 目录字符串
施加载荷的轴。
- 顺序整数
应用载荷的顺序。 - 对于点载荷,order=-1 - 对于恒定分布载荷,order=0 - 对于斜坡载荷,order=1 - 对于抛物线斜坡载荷,order=2 - … 以此类推。
- apply_moment_load(
- value,
- start,
- order,
- dir='y',
此方法将力矩载荷加到特定的梁对象上。
- 参数:
- 值Sympifyable
施加力矩的大小。
- 目录字符串
施加力矩的轴。
- 顺序整数
应用载荷的顺序。 - 对于点矩,order=-2 - 对于恒定分布矩,order=-1 - 对于斜坡矩,order=0 - 对于抛物线斜坡矩,order=1 - … 以此类推。
- property area¶
梁的横截面积。
- property boundary_conditions¶
返回一个应用于梁的边界条件字典。该字典有两个关键词,即 slope 和 deflection。每个关键词的值是一个元组列表,其中每个元组包含边界条件的位置和值,格式为 (位置, 值)。进一步地,每个值是对应于该位置沿三个轴的斜率或挠度值的列表。
示例
有一根长度为4米的梁。在0处,沿x轴的斜率为4,沿其他轴的斜率为0。在梁的另一端,沿所有三个轴的偏转应为零。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(30, E, G, I, A, x) >>> b.bc_slope = [(0, (4, 0, 0))] >>> b.bc_deflection = [(4, [0, 0, 0])] >>> b.boundary_conditions {'bending_moment': [], 'deflection': [(4, [0, 0, 0])], 'shear_force': [], 'slope': [(0, (4, 0, 0))]}
在这里,梁的偏转在
4处应沿所有三个轴为0。同样,梁的斜率在0处应沿 x 轴为4,沿 y 轴和 z 轴为0。
- property load_vector¶
返回一个表示载荷向量的三元素列表。
- max_bending_moment()[源代码][源代码]¶
返回 Beam 对象中所有方向上的最大弯矩点及其对应的弯矩值,作为一个列表返回。在使用此函数之前,必须先调用 solve_for_reaction_loads()。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, 40, 21, 100, 25, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.max_bending_moment() [(0, 0), (20, 3000), (20, 16000)]
- max_bmoment()[源代码]¶
返回 Beam 对象中所有方向上的最大弯矩点及其对应的弯矩值,作为一个列表返回。在使用此函数之前,必须先调用 solve_for_reaction_loads()。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, 40, 21, 100, 25, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.max_bending_moment() [(0, 0), (20, 3000), (20, 16000)]
- max_deflection()[源代码][源代码]¶
返回梁对象中所有方向上的最大挠度点及其对应的挠度值,作为一个列表。在使用此函数之前,必须先调用 solve_for_reaction_loads() 和 solve_slope_deflection()。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, 40, 21, 100, 25, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.solve_slope_deflection() >>> b.max_deflection() [(0, 0), (10, 495/14), (-10 + 10*sqrt(10793)/43, (10 - 10*sqrt(10793)/43)**3/160 - 20/7 + (10 - 10*sqrt(10793)/43)**4/6400 + 20*sqrt(10793)/301 + 27*(10 - 10*sqrt(10793)/43)**2/560)]
- max_shear_force()[源代码][源代码]¶
返回沿梁对象所有方向的最大剪切力点及其对应的剪切值,作为列表返回。在使用此函数之前,必须先调用 solve_for_reaction_loads()。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, 40, 21, 100, 25, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.max_shear_force() [(0, 0), (20, 2400), (20, 300)]
- property moment_load_vector¶
返回一个三元素列表,表示梁上的力矩载荷。
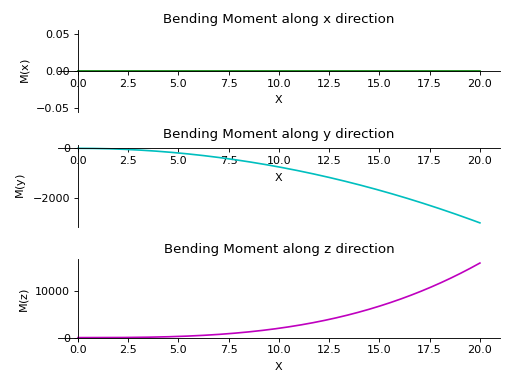
- plot_bending_moment(dir='all', subs=None)[源代码][源代码]¶
返回沿 Beam 对象中所有三个方向的弯矩图。
- 参数:
- 目录字符串 (默认)“全部”)
需要绘制弯矩图的方向。如果未指定方向,则显示所有图。
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, E, G, I, A, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.plot_bending_moment() PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: 0 for x over (0.0, 20.0) Plot[1]:Plot object containing: [0]: cartesian line: -15*x**2/2 for x over (0.0, 20.0) Plot[2]:Plot object containing: [0]: cartesian line: 2*x**3 for x over (0.0, 20.0)
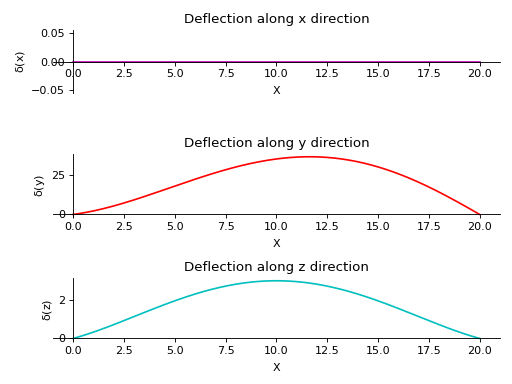
- plot_deflection(dir='all', subs=None)[源代码][源代码]¶
返回一个针对 Beam 对象中所有三个方向的偏转图。
- 参数:
- 目录字符串 (默认)“全部”)
需要偏转图的方向。如果没有指定方向,则显示所有图。
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, 40, 21, 100, 25, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.solve_slope_deflection() >>> b.plot_deflection() PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: 0 for x over (0.0, 20.0) Plot[1]:Plot object containing: [0]: cartesian line: x**5/40000 - 4013*x**3/90300 + 26*x**2/43 + 1520*x/903 for x over (0.0, 20.0) Plot[2]:Plot object containing: [0]: cartesian line: x**4/6400 - x**3/160 + 27*x**2/560 + 2*x/7 for x over (0.0, 20.0)
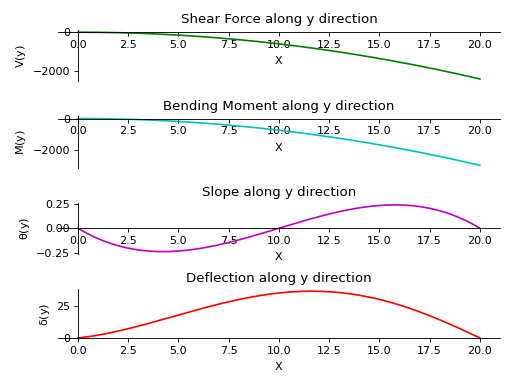
- plot_loading_results(dir='x', subs=None)[源代码][源代码]¶
返回指定方向上梁对象的剪力、弯矩、斜率和挠度的子图。
- 参数:
- 目录字符串 (默认)
x 所需的绘图方向。如果没有指定方向,则显示沿x轴的图。
- subs字典
包含符号作为键及其对应值的Python字典。
- 目录字符串 (默认)
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, E, G, I, A, x) >>> subs = {E:40, G:21, I:100, A:25} >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.solve_slope_deflection() >>> b.plot_loading_results('y',subs) PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: -6*x**2 for x over (0.0, 20.0) Plot[1]:Plot object containing: [0]: cartesian line: -15*x**2/2 for x over (0.0, 20.0) Plot[2]:Plot object containing: [0]: cartesian line: -x**3/1600 + 3*x**2/160 - x/8 for x over (0.0, 20.0) Plot[3]:Plot object containing: [0]: cartesian line: x**5/40000 - 4013*x**3/90300 + 26*x**2/43 + 1520*x/903 for x over (0.0, 20.0)
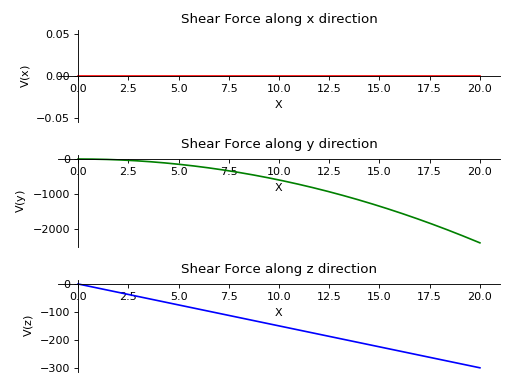
- plot_shear_force(dir='all', subs=None)[源代码][源代码]¶
返回一个沿梁对象中所有三个方向的剪力图。
- 参数:
- 目录字符串 (默认)“全部”)
需要绘制剪力图的方向。如果未指定方向,则显示所有图。
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, E, G, I, A, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.plot_shear_force() PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: 0 for x over (0.0, 20.0) Plot[1]:Plot object containing: [0]: cartesian line: -6*x**2 for x over (0.0, 20.0) Plot[2]:Plot object containing: [0]: cartesian line: -15*x for x over (0.0, 20.0)
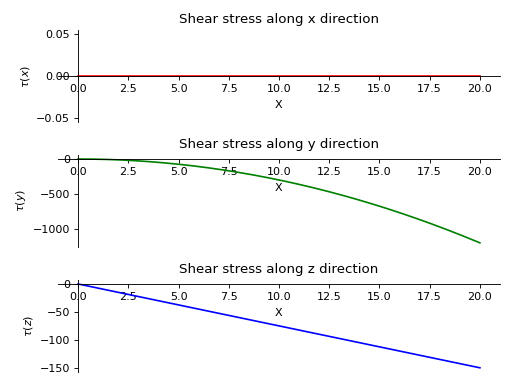
- plot_shear_stress(dir='all', subs=None)[源代码][源代码]¶
返回一个沿梁对象中所有三个方向的剪应力图。
- 参数:
- 目录字符串 (默认)“全部”)
需要绘制剪应力图的方向。如果未指定方向,则显示所有图。
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为20米、横截面积为2平方米的梁。它的两端由滚轮支撑。沿y轴施加斜率为12的线性载荷。沿z轴从起点到终点施加大小为15牛的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, E, G, I, 2, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.plot_shear_stress() PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: 0 for x over (0.0, 20.0) Plot[1]:Plot object containing: [0]: cartesian line: -3*x**2 for x over (0.0, 20.0) Plot[2]:Plot object containing: [0]: cartesian line: -15*x/2 for x over (0.0, 20.0)
- plot_slope(dir='all', subs=None)[源代码][源代码]¶
返回一个沿 Beam 对象中所有三个方向的斜率图。
- 参数:
- 目录字符串 (默认)“全部”)
需要绘制斜率图的方向。如果没有指定方向,则显示所有图。
- subs字典
包含符号作为键及其对应值的Python字典。
示例
有一根长度为20米的梁。它的两端由滚轮支撑。沿y轴施加了一个斜率为12的线性载荷。沿z轴从起点到终点施加了一个大小为15N的恒定分布载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, 40, 21, 100, 25, x) >>> b.apply_load(15, start=0, order=0, dir="z") >>> b.apply_load(12*x, start=0, order=0, dir="y") >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="z") >>> b.apply_load(R2, start=20, order=-1, dir="z") >>> b.apply_load(R3, start=0, order=-1, dir="y") >>> b.apply_load(R4, start=20, order=-1, dir="y") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.solve_slope_deflection() >>> b.plot_slope() PlotGrid object containing: Plot[0]:Plot object containing: [0]: cartesian line: 0 for x over (0.0, 20.0) Plot[1]:Plot object containing: [0]: cartesian line: -x**3/1600 + 3*x**2/160 - x/8 for x over (0.0, 20.0) Plot[2]:Plot object containing: [0]: cartesian line: x**4/8000 - 19*x**2/172 + 52*x/43 for x over (0.0, 20.0)
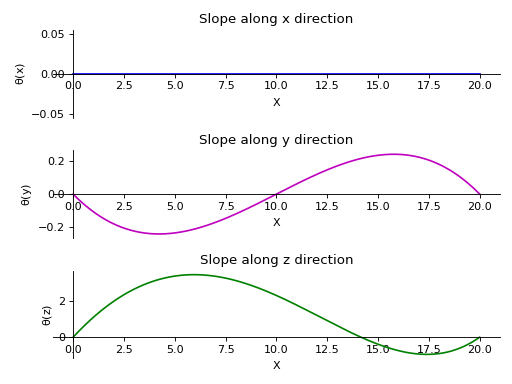
- polar_moment()[源代码][源代码]¶
返回梁相对于质心的X轴的极惯性矩。
示例
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A = symbols('l, E, G, I, A') >>> b = Beam3D(l, E, G, I, A) >>> b.polar_moment() 2*I >>> I1 = [9, 15] >>> b = Beam3D(l, E, G, I1, A) >>> b.polar_moment() 24
- property second_moment¶
梁的惯性矩。
- property shear_modulus¶
梁的杨氏模量。
- solve_for_reaction_loads(*reaction)[源代码][源代码]¶
求解反作用力。
示例
有一根长度为30米的梁。它的两端由滚轮支撑。从起点到终点沿y轴施加一个大小为8N的恒定分布载荷。沿z轴施加一个斜率为9的线性载荷。
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(30, E, G, I, A, x) >>> b.apply_load(8, start=0, order=0, dir="y") >>> b.apply_load(9*x, start=0, order=0, dir="z") >>> b.bc_deflection = [(0, [0, 0, 0]), (30, [0, 0, 0])] >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4') >>> b.apply_load(R1, start=0, order=-1, dir="y") >>> b.apply_load(R2, start=30, order=-1, dir="y") >>> b.apply_load(R3, start=0, order=-1, dir="z") >>> b.apply_load(R4, start=30, order=-1, dir="z") >>> b.solve_for_reaction_loads(R1, R2, R3, R4) >>> b.reaction_loads {R1: -120, R2: -120, R3: -1350, R4: -2700}
- solve_for_torsion()[源代码][源代码]¶
求解由于在x方向(即进出梁的方向)施加的力矩引起的扭转效应导致的角偏转。
在这里,正扭矩意味着扭矩的方向是正的,即沿着梁轴线从梁中出来。同样,负扭矩表示扭矩进入梁的横截面。
示例
>>> from sympy.physics.continuum_mechanics.beam import Beam3D >>> from sympy import symbols >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x') >>> b = Beam3D(20, E, G, I, A, x) >>> b.apply_moment_load(4, 4, -2, dir='x') >>> b.apply_moment_load(4, 8, -2, dir='x') >>> b.apply_moment_load(4, 8, -2, dir='x') >>> b.solve_for_torsion() >>> b.angular_deflection().subs(x, 3) 18/(G*I)