生物力学模型示例¶
sympy.physics.biomechanics provides features to enhance models created
with sympy.physics.mechanics with force producing elements that model
muscles and tendons. In this tutorial, we will introduce the features of this
package by adding muscles to a simple model of a human arm that moves a lever.
模型描述¶
示意图显示了杠杆 \(A\) 以及上臂 \(C\) 和下臂 \(D\)。¶
杠杆 \(A\) 可以绕 \(\hat{n}_z\) 轴旋转角度 \(q_1\)。其质心位于旋转轴上。肩部位于 \(P_2\),上臂 \(C\) 可以绕 \(\hat{n}_y\) 轴延伸角度 \(q_2\),并绕 \(\hat{b}_z\) 轴旋转角度 \(q_3\)。肘部位于点 \(P_3\)。前臂可以绕 \(\hat{c}_y\) 轴弯曲角度 \(q_4\)。手位于点 \(P_4\)。手将被约束在杠杆上,通过强制 \(\mathbf{r}^{P_4/O} = \mathbf{r}^{P_1/O}\)。杠杆、上臂和前臂将被建模为薄圆柱体,以简化惯性计算。
我们将介绍两个肌腱模型,分别代表肱二头肌和肱三头肌。两个肌肉附着点 \(C_m\) 和 \(D_m\) 分别固定在上臂和下臂上。肱二头肌将沿着从 \(C_m\) 到 \(D_m\) 的直线作用,当收缩时会导致肘部弯曲。定义一个半径为 \(r\) 的圆弧,其中心在 \(P_3\),且法线方向为 \(\hat{c}_y\)。肱三头肌将围绕该圆弧包裹,并附着在与肱二头肌相同的点上,当收缩时会导致肘部伸展。
>>> import sympy as sm
>>> import sympy.physics.mechanics as me
>>> import sympy.physics.biomechanics as bm
定义变量¶
介绍用于杠杆角度、肩部伸展、肩部旋转和肘部屈曲的四个坐标 \(\mathbf{q} = [q_1, q_2, q_3, q_4]^T\)。我们还需要广义速度 \(\mathbf{u} = [u_1,u_2,u_3,u_4]^T\),我们将其定义为 \(\mathbf{u} = \dot{\mathbf{q}}\)。
>>> q1, q2, q3, q4 = me.dynamicsymbols('q1, q2, q3, q4', real=True)
>>> u1, u2, u3, u4 = me.dynamicsymbols('u1, u2, u3, u4', real=True)
机械系统所需的常量参数包括:
\(d_x, l_A\): 分别沿 \(\hat{n}_x\) 和 \(\hat{a}_y\) 方向从 \(O\) 定位 \(P_1\)
\(d_y, d_z\): 沿着 \(N\) 单位向量方向从 \(O\) 定位 \(P_2\)
\(l_C,l_D\) : 上臂和下臂的长度
\(m_A,m_C,m_D\) : 杠杆、上臂和下臂的质量
\(g\) : 重力加速度
\(k\) : 杠杆线性旋转弹簧系数
\(c\) : 杠杆线性旋转阻尼系数
>>> dx, dy, dz = sm.symbols('dx, dy, dz', real=True, nonnegative=True)
>>> lA, lC, lD = sm.symbols('lA, lC, lD', real=True, positive=True)
>>> mA, mC, mD = sm.symbols('mA, mC, mD', real=True, positive=True)
>>> g, k, c, r = sm.symbols('g, k, c, r', real=True, positive=True)
定义运动学¶
定义 示意图显示了杠杆 A 以及上臂 C 和下臂 D。 中显示的所有参考框架和点。\(C_o\) 和 \(D_o\) 分别是上臂和下臂的质量中心。
>>> N, A, B, C, D = sm.symbols('N, A, B, C, D', cls=me.ReferenceFrame)
>>> O, P1, P2, P3, P4 = sm.symbols('O, P1, P2, P3, P4 ', cls=me.Point)
>>> Ao, Co, Cm, Dm, Do = sm.symbols('Ao, Co, Cm, Dm, Do', cls=me.Point)
参考坐标系的方向和角速度为:
>>> A.orient_axis(N, q1, N.z)
>>> B.orient_axis(N, q2, N.y)
>>> C.orient_axis(B, q3, B.z)
>>> D.orient_axis(C, q4, C.y)
>>> A.set_ang_vel(N, u1*N.z)
>>> B.set_ang_vel(N, u2*N.y)
>>> C.set_ang_vel(B, u3*B.z)
>>> D.set_ang_vel(C, u4*C.y)
所有点的位置和速度如下:
>>> Ao.set_pos(O, dx*N.x)
>>> P1.set_pos(Ao, lA*A.y)
>>> P2.set_pos(O, dy*N.y + dz*N.z)
>>> Co.set_pos(P2, lC/2*C.z)
>>> Cm.set_pos(P2, 1*lC/3*C.z)
>>> P3.set_pos(P2, lC*C.z)
>>> Dm.set_pos(P3, 1*lD/3*D.z)
>>> Do.set_pos(P3, lD/2*D.z)
>>> P4.set_pos(P3, lD*D.z)
>>> O.set_vel(N, 0)
>>> Ao.set_vel(N, 0)
>>> P1.v2pt_theory(Ao, N, A)
- lA*u1(t)*A.x
>>> P2.set_vel(N, 0)
>>> Co.v2pt_theory(P2, N, C)
lC*u2(t)*cos(q3(t))/2*C.x - lC*u2(t)*sin(q3(t))/2*C.y
>>> Cm.v2pt_theory(P2, N, C)
lC*u2(t)*cos(q3(t))/3*C.x - lC*u2(t)*sin(q3(t))/3*C.y
>>> P3.v2pt_theory(P2, N, C)
lC*u2(t)*cos(q3(t))*C.x - lC*u2(t)*sin(q3(t))*C.y
>>> Dm.v2pt_theory(P3, N, D)
lC*u2(t)*cos(q3(t))*C.x - lC*u2(t)*sin(q3(t))*C.y + lD*(u2(t)*cos(q3(t)) + u4(t))/3*D.x - lD*(u2(t)*sin(q3(t))*cos(q4(t)) - u3(t)*sin(q4(t)))/3*D.y
>>> Do.v2pt_theory(P3, N, D)
lC*u2(t)*cos(q3(t))*C.x - lC*u2(t)*sin(q3(t))*C.y + lD*(u2(t)*cos(q3(t)) + u4(t))/2*D.x - lD*(u2(t)*sin(q3(t))*cos(q4(t)) - u3(t)*sin(q4(t)))/2*D.y
>>> P4.v2pt_theory(P3, N, D)
lC*u2(t)*cos(q3(t))*C.x - lC*u2(t)*sin(q3(t))*C.y + lD*(u2(t)*cos(q3(t)) + u4(t))*D.x - lD*(u2(t)*sin(q3(t))*cos(q4(t)) - u3(t)*sin(q4(t)))*D.y
需要三个完整约束方程来保持手 \(P_4\) 在杠杆 \(P_1\) 上:
>>> holonomic = (P4.pos_from(O) - P1.pos_from(O)).to_matrix(N)
定义惯性¶
假设杠杆、上臂和下臂为薄圆柱体,可以形成惯性二元组和刚体:
>>> IA = me.Inertia(me.inertia(A, mA/12*lA**2, mA/2*lA**2, mA/12*lA**2), Ao)
>>> IC = me.Inertia(me.inertia(C, mC/12*lC**2, mC/12*lC**2, mC/2*lC**2), Co)
>>> ID = me.Inertia(me.inertia(D, mD/12*lD**2, mD/12*lD**2, mD/2*lD**2), Do)
>>> lever = me.RigidBody('lever', masscenter=Ao, frame=A, mass=mA, inertia=IA)
>>> u_arm = me.RigidBody('upper arm', masscenter=Co, frame=C, mass=mC, inertia=IC)
>>> l_arm = me.RigidBody('lower arm', masscenter=Do, frame=D, mass=mD, inertia=ID)
定义力¶
我们将在地球的重力场中模拟这个系统:
>>> gravC = me.Force(u_arm, mC*g*N.z)
>>> gravD = me.Force(l_arm, mD*g*N.z)
杠杆具有惯性,但我们还将添加一个线性扭转弹簧和阻尼器,以提供更多的阻力,使手臂按压和拉动时能感受到阻力:
>>> lever_resistance = me.Torque(A, (-k*q1 - c*u1)*N.z)
二头肌¶
We will model the biceps muscle as an actuator that contracts between the two
muscle attachment points \(C_m\) and \(D_m\). This muscle can contract
given an excitation specified input and we will assume that the associated
tendon is rigid. The musculotendon actuator model will be made up of two
components: a pathway on which to act and activation dynamics that define how
an excitation input will propagate to activating the muscle. The biceps muscle
will act along a LinearPathway and will
use a specific muscle dynamics implementation derived from [DeGroote2016].
首先创建线性路径:
>>> biceps_pathway = me.LinearPathway(Cm, Dm)
你可以创建一个完全符号化的激活模型,或者使用 [DeGroote2016] 中的特定调优数值参数来创建它(推荐):
>>> biceps_activation = bm.FirstOrderActivationDeGroote2016.with_defaults('biceps')
完整的肌肉肌腱执行器模型随后被命名并使用匹配的类进行构建:
>>> biceps = bm.MusculotendonDeGroote2016.with_defaults('biceps', biceps_pathway, biceps_activation)
Triceps¶
三头肌执行器模型需要一个自定义路径来管理肌肉和肌腱围绕半径为 \(r\) 的圆弧的包裹特性。该路径由两个长度不变的直线段和一个随着肘部伸展和屈曲而改变长度的圆弧组成。作用在上臂和下臂上的力可以被建模为作用在点 \(C_m\) 和 \(D_m\) 上的力,这些力始终平行于直线段,以及从作用在圆弧末端点的等大反向力产生的在点 \(P_3\) 的合力。
To develop this pathway we need to subclass
PathwayBase and create methods that
compute the pathway length, pathway extension velocity, and the loads acting on
the involved bodies. We will develop a class which assumes that there is a pin
joint between two rigid bodies, that the two muscle attachment points are fixed
on each body, respectively, and that the pin joint point and two attachment
points lie in the same plane which is normal to the pin joint axis. We will
also assume that the pin joint coordinate is measured as \(q_4\) is in
示意图显示了杠杆 A 以及上臂 C 和下臂 D。 and that \(0 \le q_4 \le \pi\)’. The
circular arc has a radius \(r\). With these assumptions we can then use the
__init__() method to collect the necessary information for use in the
remaining methods. In __init__() we will also calculate some quantities
that will be needed in multiple overloaded methods. The length of the pathway
is the sum of the lengths of the two linear segments and the circular arc that
changes with variation of the pin joint coordinate. The extension velocity is
simply the change with respect to time in the arc length. The loads are made up
of three forces: two that push an pull on the origin and insertion points along
the linear portions of the pathway and the resultant effect on the elbow from
the forces pushing and pulling on the ends of the circular arc.
>>> class ExtensorPathway(me.PathwayBase):
...
... def __init__(self, origin, insertion, axis_point, axis, parent_axis,
... child_axis, radius, coordinate):
... """A custom pathway that wraps a circular arc around a pin joint.
...
... This is intended to be used for extensor muscles. For example, a
... triceps wrapping around the elbow joint to extend the upper arm at
... the elbow.
...
... Parameters
... ==========
... origin : Point
... Muscle origin point fixed on the parent body (A).
... insertion : Point
... Muscle insertion point fixed on the child body (B).
... axis_point : Point
... Pin joint location fixed in both the parent and child.
... axis : Vector
... Pin joint rotation axis.
... parent_axis : Vector
... Axis fixed in the parent frame (A) that is directed from the pin
... joint point to the muscle origin point.
... child_axis : Vector
... Axis fixed in the child frame (B) that is directed from the pin
... joint point to the muscle insertion point.
... radius : sympyfiable
... Radius of the arc that the muscle wraps around.
... coordinate : sympfiable function of time
... Joint angle, zero when parent and child frames align. Positive
... rotation about the pin joint axis, B with respect to A.
...
... Notes
... =====
...
... Only valid for coordinate >= 0.
...
... """
... super().__init__(origin, insertion)
...
... self.origin = origin
... self.insertion = insertion
... self.axis_point = axis_point
... self.axis = axis.normalize()
... self.parent_axis = parent_axis.normalize()
... self.child_axis = child_axis.normalize()
... self.radius = radius
... self.coordinate = coordinate
...
... self.origin_distance = axis_point.pos_from(origin).magnitude()
... self.insertion_distance = axis_point.pos_from(insertion).magnitude()
... self.origin_angle = sm.asin(self.radius/self.origin_distance)
... self.insertion_angle = sm.asin(self.radius/self.insertion_distance)
...
... @property
... def length(self):
... """Length of the pathway.
...
... Length of two fixed length line segments and a changing arc length
... of a circle.
...
... """
...
... angle = self.origin_angle + self.coordinate + self.insertion_angle
... arc_length = self.radius*angle
...
... origin_segment_length = self.origin_distance*sm.cos(self.origin_angle)
... insertion_segment_length = self.insertion_distance*sm.cos(self.insertion_angle)
...
... return origin_segment_length + arc_length + insertion_segment_length
...
... @property
... def extension_velocity(self):
... """Extension velocity of the pathway.
...
... Arc length of circle is the only thing that changes when the elbow
... flexes and extends.
...
... """
... return self.radius*self.coordinate.diff(me.dynamicsymbols._t)
...
... def to_loads(self, force_magnitude):
... """Loads in the correct format to be supplied to `KanesMethod`.
...
... Forces applied to origin, insertion, and P from the muscle wrapped
... over circular arc of radius r.
...
... """
...
... parent_tangency_point = me.Point('Aw') # fixed in parent
... child_tangency_point = me.Point('Bw') # fixed in child
...
... parent_tangency_point.set_pos(
... self.axis_point,
... -self.radius*sm.cos(self.origin_angle)*self.parent_axis.cross(self.axis)
... + self.radius*sm.sin(self.origin_angle)*self.parent_axis,
... )
... child_tangency_point.set_pos(
... self.axis_point,
... self.radius*sm.cos(self.insertion_angle)*self.child_axis.cross(self.axis)
... + self.radius*sm.sin(self.insertion_angle)*self.child_axis),
...
... parent_force_direction_vector = self.origin.pos_from(parent_tangency_point)
... child_force_direction_vector = self.insertion.pos_from(child_tangency_point)
... force_on_parent = force_magnitude*parent_force_direction_vector.normalize()
... force_on_child = force_magnitude*child_force_direction_vector.normalize()
... loads = [
... me.Force(self.origin, force_on_parent),
... me.Force(self.axis_point, -(force_on_parent + force_on_child)),
... me.Force(self.insertion, force_on_child),
... ]
... return loads
...
既然我们已经定义了一个自定义路径,我们可以以与二头肌相同的方式创建一个肌腱肌模型:
>>> triceps_pathway = ExtensorPathway(Cm, Dm, P3, B.y, -C.z, D.z, r, q4)
>>> triceps_activation = bm.FirstOrderActivationDeGroote2016.with_defaults('triceps')
>>> triceps = bm.MusculotendonDeGroote2016.with_defaults('triceps', triceps_pathway, triceps_activation)
最后,所有的负载可以被组装成一个列表:
>>> loads = biceps.to_loads() + triceps.to_loads() + [lever_resistance, gravC, gravD]
运动方程¶
现在所有载荷都已定义,可以生成系统的运动方程。我们有三个完整约束,因此系统只有一个自由度。
>>> kane = me.KanesMethod(
... N,
... (q1,),
... (u1,),
... kd_eqs=(
... u1 - q1.diff(),
... u2 - q2.diff(),
... u3 - q3.diff(),
... u4 - q4.diff(),
... ),
... q_dependent=(q2, q3, q4),
... configuration_constraints=holonomic,
... velocity_constraints=holonomic.diff(me.dynamicsymbols._t),
... u_dependent=(u2, u3, u4),
... )
...
>>> Fr, Frs = kane.kanes_equations((lever, u_arm, l_arm), loads)
非线性项中的 \(\dot{\mathbf{u}}\) 包含了肌肉力,这些力是激活状态变量的函数,除了坐标和广义速度外。
>>> me.find_dynamicsymbols(kane.forcing)
{a_biceps(t), a_triceps(t), q1(t), q2(t), q3(t), q4(t), u1(t), u2(t), u3(t), u4(t)}
它们还包含与肌肉模型相关的新常量参数:
>>> kane.forcing.free_symbols
{F_M_max_biceps, F_M_max_triceps, c, g, k, lA, lC, lD, l_M_opt_biceps, l_M_opt_triceps, l_T_slack_biceps, l_T_slack_triceps, mC, mD, r, t}
肌肉激活微分方程¶
每个肌肉的激活状态是与两个新的常微分方程相关联的新状态变量。这些微分方程从肌肉执行器模型中获取:
>>> biceps.rhs()
Matrix([[((1/2 - tanh(10.0*a_biceps(t) - 10.0*e_biceps(t))/2)/(0.0225*a_biceps(t) + 0.0075) + 16.6666666666667*(3*a_biceps(t)/2 + 1/2)*(tanh(10.0*a_biceps(t) - 10.0*e_biceps(t))/2 + 1/2))*(-a_biceps(t) + e_biceps(t))]])
>>> triceps.rhs()
Matrix([[((1/2 - tanh(10.0*a_triceps(t) - 10.0*e_triceps(t))/2)/(0.0225*a_triceps(t) + 0.0075) + 16.6666666666667*(3*a_triceps(t)/2 + 1/2)*(tanh(10.0*a_triceps(t) - 10.0*e_triceps(t))/2 + 1/2))*(-a_triceps(t) + e_triceps(t))]])
将肌肉激活微分方程一起存储在一个矩阵中:
>>> dadt = biceps.rhs().col_join(triceps.rhs())
评估系统微分方程¶
该系统的完整微分方程组的形式为:
在这种情况下,只有动力学微分方程需要求解线性系统以转换为显式形式。
To evaluate the system’s equations we first need to gather up all of the state,
input, and constant variables for use with
lambdify. The state vector is made up of the
coordinates, generalized speeds, and the two muscles’ activation state:
\(\mathbf{x}=\begin{bmatrix}\mathbf{q}\\\mathbf{u}\\\mathbf{a}\end{bmatrix}\).
>>> q, u = kane.q, kane.u
>>> a = biceps.x.col_join(triceps.x)
>>> x = q.col_join(u).col_join(a)
>>> x
Matrix([
[ q1(t)],
[ q2(t)],
[ q3(t)],
[ q4(t)],
[ u1(t)],
[ u2(t)],
[ u3(t)],
[ u4(t)],
[ a_biceps(t)],
[a_triceps(t)]])
唯一指定的输入是两个肌肉的兴奋:
>>> e = biceps.r.col_join(triceps.r)
>>> e
Matrix([
[ e_biceps(t)],
[e_triceps(t)]])
常数由几何形状、质量、局部重力常数、杠杆的刚度和阻尼系数以及肌肉的各种参数组成。
>>> p = sm.Matrix([
... dx,
... dy,
... dz,
... lA,
... lC,
... lD,
... mA,
... mC,
... mD,
... g,
... k,
... c,
... r,
... biceps.F_M_max,
... biceps.l_M_opt,
... biceps.l_T_slack,
... triceps.F_M_max,
... triceps.l_M_opt,
... triceps.l_T_slack,
... ])
...
>>> p
Matrix([
[ dx],
[ dy],
[ dz],
[ lA],
[ lC],
[ lD],
[ mA],
[ mC],
[ mD],
[ g],
[ k],
[ c],
[ r],
[ F_M_max_biceps],
[ l_M_opt_biceps],
[ l_T_slack_biceps],
[ F_M_max_triceps],
[ l_M_opt_triceps],
[l_T_slack_triceps]])
现在我们有了所有符号组件来生成数值函数以评估 \(\mathbf{M}_d,\mathbf{g}_d\) 和 \(\mathbf{g}_a\)。通过这些我们可以计算状态的时间导数。我们还需要一个数值函数来处理完整约束,以确保配置处于有效状态。
>>> eval_diffeq = sm.lambdify((q, u, a, e, p),
... (kane.mass_matrix, kane.forcing, dadt), cse=True)
>>> eval_holonomic = sm.lambdify((q, p), holonomic, cse=True)
我们需要为所有常量设定一些合理的数值:
>>> import numpy as np
>>> p_vals = np.array([
... 0.31, # dx [m]
... 0.15, # dy [m]
... -0.31, # dz [m]
... 0.2, # lA [m]
... 0.3, # lC [m]
... 0.3, # lD [m]
... 1.0, # mA [kg]
... 2.3, # mC [kg]
... 1.7, # mD [kg]
... 9.81, # g [m/s/s]
... 5.0, # k [Nm/rad]
... 0.5, # c [Nms/rad]
... 0.03, # r [m]
... 500.0, # biceps F_M_max [?]
... 0.6*0.3, # biceps l_M_opt [?]
... 0.55*0.3, # biceps l_T_slack [?]
... 500.0, # triceps F_M_max [?]
... 0.6*0.3, # triceps l_M_opt [?]
... 0.65*0.3, # triceps l_T_slack [?]
... ])
...
由于三个完整约束,三个坐标是其余一个坐标的函数。我们可以选择杠杆角度 \(q_1\) 作为独立坐标,并在给定其值的猜测下求解其余坐标。
>>> from scipy.optimize import fsolve
>>> q_vals = np.array([
... np.deg2rad(5.0), # q1 [rad]
... np.deg2rad(-10.0), # q2 [rad]
... np.deg2rad(0.0), # q3 [rad]
... np.deg2rad(75.0), # q4 [rad]
... ])
...
>>> def eval_holo_fsolve(x):
... q1 = q_vals[0] # specified
... q2, q3, q4 = x
... return eval_holonomic((q1, q2, q3, q4), p_vals).squeeze()
...
>>> q_vals[1:] = fsolve(eval_holo_fsolve, q_vals[1:])
>>> np.rad2deg(q_vals)
[ 5. -0.60986636 9.44918589 88.68812842]
我们假设系统处于初始静止状态:
>>> u_vals = np.array([
... 0.0, # u1, [rad/s]
... 0.0, # u2, [rad/s]
... 0.0, # u3, [rad/s]
... 0.0, # u4, [rad/s]
... ])
...
>>> a_vals = np.array([
... 0.0, # a_bicep, nondimensional
... 0.0, # a_tricep, nondimensional
... ])
肌肉兴奋也将最初被停用:
>>> e_vals = np.array([
... 0.0,
... 0.0,
... ])
系统方程现在可以进行数值评估:
>>> eval_diffeq(q_vals, u_vals, a_vals, e_vals, p_vals)
([[ 0.00333333 -0.15174161 -0.00109772 -0.00152436]
[ 0.19923894 0.31 -0.04923615 0.00996712]
[ 0.01743115 0. 0.29585191 0.0011276 ]
[ 0. -0.29256885 -0.0005241 -0.29983226]], [[-0.9121071]
[ 0. ]
[-0. ]
[ 0. ]], [[0.]
[0.]])
模拟肌肉驱动的运动¶
现在,给定状态和常数值,我们可以评估系统方程,从而模拟手臂和杠杆在两块肌肉刺激下的运动。如果提供一个以显式形式评估方程的函数,即 \(\dot{\mathbf{x}}=\),SciPy 的 solve_ivp() 可以积分微分方程。我们将包含一个刺激肌肉的函数,但在第一次模拟中将其设置为零。
>>> def eval_r(t):
... """Returns the muscles' excitation as a function of time."""
... e = np.array([0.0, 0.0])
... return e
...
>>> def eval_rhs(t, x, r, p):
... """Returns the time derivative of the state.
...
... Parameters
... ==========
... t : float
... Time in seconds.
... x : array_like, shape(10,)
... State vector.
... r : function
... Function f(t) that evaluates e.
... p : array_like, shape(?, )
... Parameter vector.
...
... Returns
... =======
... dxdt : ndarray, shape(10,)
... Time derivative of the state.
...
... """
...
... q = x[0:4]
... u = x[4:8]
... a = x[8:10]
...
... e = r(t)
...
... qd = u
... m, f, ad = eval_diffeq(q, u, a, e, p)
... ud = np.linalg.solve(m, f).squeeze()
...
... return np.hstack((qd, ud, ad.squeeze()))
...
系统现在可以在给定初始状态 \(\mathbf{x}_0\) 和上述定义的函数的情况下,使用 SciPy 的 solve_ivp() 进行 3 秒的模拟。
>>> from scipy.integrate import solve_ivp
>>> t0, tf = 0.0, 3.0
>>> ts = np.linspace(t0, tf, num=301)
>>> x0 = np.hstack((q_vals, u_vals, a_vals))
>>> sol = solve_ivp(lambda t, x: eval_rhs(t, x, eval_r, p_vals),
... (t0, tf), x0, t_eval=ts)
通过绘制状态轨迹随时间的变化,可以直观地看到运动情况:
>>> import matplotlib.pyplot as plt
>>> def plot_traj(t, x, syms):
... """Simple plot of state trajectories.
...
... Parameters
... ==========
... t : array_like, shape(n,)
... Time values.
... x : array_like, shape(n, m)
... State values at each time value.
... syms : sequence of Symbol, len(m)
... SymPy symbols associated with state.
...
... """
...
... fig, axes = plt.subplots(5, 2, sharex=True)
...
... for ax, traj, sym in zip(axes.T.flatten(), x.T, syms):
... if not sym.name.startswith('a'):
... traj = np.rad2deg(traj)
... ax.plot(t, traj)
... ax.set_ylabel(sm.latex(sym, mode='inline'))
...
... for ax in axes[-1, :]:
... ax.set_xlabel('Time [s]')
...
... fig.tight_layout()
...
... return axes
...
>>> plot_traj(ts, sol.y.T, x)
[[<Axes: ylabel='$q_{1}{\\left(t \\right)}$'>
<Axes: ylabel='$u_{2}{\\left(t \\right)}$'>]
[<Axes: ylabel='$q_{2}{\\left(t \\right)}$'>
<Axes: ylabel='$u_{3}{\\left(t \\right)}$'>]
[<Axes: ylabel='$q_{3}{\\left(t \\right)}$'>
<Axes: ylabel='$u_{4}{\\left(t \\right)}$'>]
[<Axes: ylabel='$q_{4}{\\left(t \\right)}$'>
<Axes: ylabel='$a_{biceps}{\\left(t \\right)}$'>]
[<Axes: xlabel='Time [s]', ylabel='$u_{1}{\\left(t \\right)}$'>
<Axes: xlabel='Time [s]', ylabel='$a_{triceps}{\\left(t \\right)}$'>]]
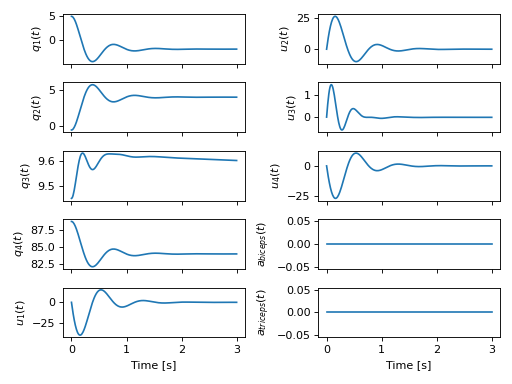
初始杠杆角度为5度的手臂模拟,在没有肌肉激活的情况下稳定到其平衡位置。¶
仿真显示,手臂在重力、杠杆阻力和肌腱模型被动因素的共同作用下达到平衡。现在我们激活肱二头肌1秒钟,激发80%,以观察其对运动的影响:
>>> def eval_r(t):
... if t < 0.5 or t > 1.5:
... e = np.array([0.0, 0.0])
... else:
... e = np.array([0.8, 0.0])
... return e
...
>>> sol = solve_ivp(lambda t, x: eval_rhs(t, x, eval_r, p_vals), (t0, tf), x0, t_eval=ts)
>>> plot_traj(ts, sol.y.T, x)
[[<Axes: ylabel='$q_{1}{\\left(t \\right)}$'>
<Axes: ylabel='$u_{2}{\\left(t \\right)}$'>]
[<Axes: ylabel='$q_{2}{\\left(t \\right)}$'>
<Axes: ylabel='$u_{3}{\\left(t \\right)}$'>]
[<Axes: ylabel='$q_{3}{\\left(t \\right)}$'>
<Axes: ylabel='$u_{4}{\\left(t \\right)}$'>]
[<Axes: ylabel='$q_{4}{\\left(t \\right)}$'>
<Axes: ylabel='$a_{biceps}{\\left(t \\right)}$'>]
[<Axes: xlabel='Time [s]', ylabel='$u_{1}{\\left(t \\right)}$'>
<Axes: xlabel='Time [s]', ylabel='$a_{triceps}{\\left(t \\right)}$'>]]
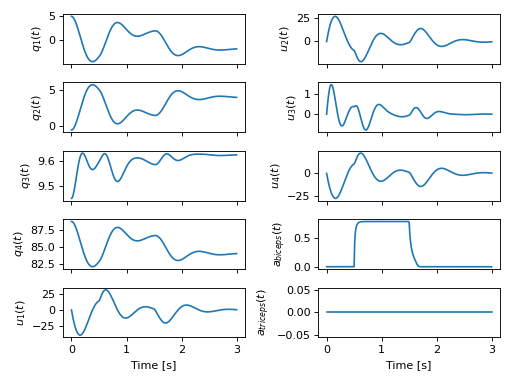
在肱二头肌收缩1秒的影响下,模拟初始杠杆角度为5度的手臂。¶
我们首先看到手臂像之前一样试图达到平衡,但随后激活的肱二头肌将杠杆拉回肩部,导致手臂对抗被动运动。一旦肌肉被停用,手臂就会像之前一样恢复。
结论¶
这里我们展示了如何通过构建一个简单且自定义的肌肉-肌腱驱动路径来创建一个代表肌肉骨骼系统的数学模型。通过刺激肌肉可以控制模型的运动,模拟显示出预期的行为。