傅里叶级数

提供计算傅里叶级数的方法。

class sympy.series.fourier.FourierSeries(*args)

表示傅里叶正弦/余弦级数。

属性:

L

a0

一个

args

返回 ‘self’ 的参数元组。

assumptions0

返回对象 \(type\) 假设。

bn

canonical_variables

返回一个字典，将 self.bound_symbols 中定义的任何变量映射到与表达式中任何自由符号不冲突的符号。

expr_free_symbols

类似于 free_symbols，但仅在自由符号包含在表达式节点中时返回它们。

free_symbols

此方法返回对象中的符号，排除那些具有特定值的符号（即

func

表达式中的顶级函数。

函数

interval

该序列定义的区间

is_algebraic

is_antihermitian

is_commutative

is_comparable

如果 self 可以计算为一个具有精度的实数（或已经是一个实数），则返回 True，否则返回 False。

is_complex

is_composite

is_even

is_extended_negative

is_extended_nonnegative

is_extended_nonpositive

is_extended_nonzero

is_extended_positive

is_extended_real

is_finite

is_hermitian

is_imaginary

is_infinite

is_integer

is_irrational

is_negative

is_noninteger

is_nonnegative

is_nonpositive

is_nonzero

is_number

如果 self 没有自由符号且没有未定义的函数（确切地说，是 AppliedUndef），则返回 True。

is_odd

is_polar

is_positive

is_prime

is_rational

is_real

is_transcendental

is_zero

length

级数展开的长度

周期

start

系列的起始点。

stop

系列的终点。

variables

返回一个变量元组，这些变量已被绑定

x

方法

apart([x])	请参阅 sympy.polys 中的 apart 函数。
args_cnc([cset, warn, split_1])	返回 [交换因子, 非交换因子] 的自身。
as_coeff_Add([rational])	高效地提取求和的系数。
as_coeff_Mul([rational])	高效地提取乘积的系数。
as_coeff_add(*deps)	返回元组 (c, args)，其中 self 被写成一个 Add，a。
as_coeff_exponent(x)	c*x**e -> c,e 其中 x 可以是任何符号表达式。
as_coeff_mul(*deps, **kwargs)	返回元组 (c, args)，其中 self 被写成一个 Mul，m。
as_coefficient(expr)	提取给定表达式中的符号系数。
as_coefficients_dict(*syms)	返回一个字典，将术语映射到它们的 Rational 系数。
as_content_primitive([radical, clear])	此方法应递归地从所有参数中移除一个 Rational，并返回该内容和新的 self（原始类型）。
as_dummy()	返回表达式，其中任何具有结构绑定符号的对象都被替换为在其出现的对象中唯一的规范符号，并且仅对交换性具有默认假设为True。
as_expr(*gens)	将多项式转换为 SymPy 表达式。
as_independent(*deps, **hint)	将 Mul 或 Add 的大部分天真分离为不依赖于 deps 的参数。
as_leading_term(*symbols[, logx, cdir])	返回自身级数展开的主导（非零）项。
as_numer_denom()	返回一个表达式的分子和分母。
as_ordered_factors([order])	返回有序因子列表（如果是 Mul），否则返回 [self]。
as_ordered_terms([order, data])	将表达式转换为有序的项列表。
as_poly(*gens, **args)	将 self 转换为多项式，或返回 None。
as_powers_dict()	将自身作为一个因子的字典返回，每个因子都被视为一个幂。
as_real_imag([deep])	对 'self' 执行复杂的扩展，并返回一个包含收集到的实部和虚部的元组。
as_terms()	将一个表达式转换为项的列表。
aseries([x, n, bound, hir])	自变量的渐近级数展开
atoms(*types)	返回构成当前对象的原子。
cancel(*gens, **args)	参见 sympy.polys 中的取消函数
class_key()	类的好顺序。
coeff(x[, n, right, _first])	返回包含 x**n 的项中的系数。
collect(syms[, func, evaluate, exact, ...])	请参阅 sympy.simplify 中的 collect 函数。
combsimp()	请参阅 sympy.simplify 中的 combsimp 函数。
compare(other)	如果对象在规范意义上小于、等于或大于其他对象，则返回 -1、0、1。
compute_leading_term(x[, logx])	已弃用的函数，用于计算级数的首项。
conjugate()	返回 'self' 的复数共轭。
could_extract_minus_sign()	如果 self 以 -1 作为前导因子，或在求和中有比正号更多的负号，则返回 True，否则返回 False。
count(query)	计算匹配的子表达式的数量。
count_ops([visual])
doit(**hints)	评估默认情况下不评估的对象，如极限、积分、求和和乘积。
dummy_eq(other[, symbol])	比较两个表达式并处理哑符号。
equals(other[, failing_expression])	如果 self == other 则返回 True，如果不相等则返回 False，或者返回 None。
evalf([n, subs, maxn, chop, strict, quad, ...])	将给定的公式计算到 n 位精度。
expand([deep, modulus, power_base, ...])	使用提示扩展表达式。
extract_additively(c)	如果可以从自身减去 c 并且使所有匹配的系数趋向于零，则返回 self - c，否则返回 None。
extract_branch_factor([allow_half])	尝试以 exp_polar(2*pi*I*n)*z 的方式优雅地表达自身。
extract_multiplicatively(c)	如果无法以一种良好的方式将 self 表示为 c * something，即保留 self 参数的属性，则返回 None。
factor(*gens, **args)	参见 sympy.polys.polytools 中的 factor() 函数
find(query[, group])	查找所有匹配查询的子表达式。
fourier_series([limits])	计算自身的傅里叶正弦/余弦级数。
fps([x, x0, dir, hyper, order, rational, full])	计算自身的形式幂级数。
fromiter(args, **assumptions)	从可迭代对象创建一个新对象。
gammasimp()	参见 sympy.simplify 中的 gammasimp 函数
getO()	如果有加法 O(..) 符号，则返回该符号，否则返回 None。
getn()	返回表达式的顺序。
has(*patterns)	测试是否有任何子表达式匹配任何模式。
has_free(*patterns)	如果 self 包含对象 x 作为自由表达式，则返回 True，否则返回 False。
has_xfree(s)	如果 self 有 s 中的任何一个模式作为自由参数，则返回 True，否则返回 False。
integrate(*args, **kwargs)	请参阅 sympy.integrals 中的 integrate 函数。
invert(g, *gens, **args)	返回 self 对 g 的乘法逆元，其中 self``（和 ``g）可以是符号表达式。
is_algebraic_expr(*syms)	此测试给定的表达式是否在给定的符号 syms 中是代数的。
is_constant(*wrt, **flags)	如果 self 是常量则返回 True，如果不是则返回 False，如果无法明确确定常量性则返回 None。
is_meromorphic(x, a)	此测试表达式是否作为给定符号 x 的函数在点 a 处是亚纯的。
is_polynomial(*syms)	如果 self 是 syms 中的多项式，则返回 True，否则返回 False。
is_rational_function(*syms)	测试函数是否为给定符号 syms 中的两个多项式的比率。
is_same(b[, approx])	如果 a 和 b 结构相同则返回 True，否则返回 False。
leadterm(x[, logx, cdir])	返回首项 a*x**b 作为元组 (a, b)。
limit(x, xlim[, dir])	计算极限 x->xlim。
lseries([x, x0, dir, logx, cdir])	用于生成序列项的迭代器的包装器。
match(pattern[, old])	模式匹配。
matches(expr[, repl_dict, old])	用于 match() 的辅助方法，用于在 self 中的通配符符号与 expr 中的表达式之间寻找匹配。
n([n, subs, maxn, chop, strict, quad, verbose])	将给定的公式计算到 n 位精度。
normal()	返回表达式为分数形式。
nseries([x, x0, n, dir, logx, cdir])	如果假设允许，包装器调用 _eval_nseries，否则调用 series。
nsimplify([constants, tolerance, full])	参见 sympy.simplify 中的 nsimplify 函数
powsimp(*args, **kwargs)	参见 sympy.simplify 中的 powsimp 函数
primitive()	返回可以从自身每个项中非递归提取的正有理数（即，将自身视为一个加法）。
radsimp(**kwargs)	参见 sympy.simplify 中的 radsimp 函数
ratsimp()	参见 sympy.simplify 中的 ratsimp 函数。
rcall(*args)	通过表达式树递归应用于参数。
refine([assumption])	请参阅 sympy.assumptions 中的 refine 函数。
removeO()	如果存在，移除加性的 O(..) 符号
replace(query, value[, map, simultaneous, exact])	将 self 中匹配的子表达式替换为 value。
rewrite(*args[, deep])	使用定义的规则重写 self。
round([n])	返回 x 四舍五入到给定的十进制位。
scale(s)	按一个与 x 无关的项缩放函数。
scalex(s)	将 x 按与 x 无关的项进行缩放。
separate([deep, force])	参见 sympy.simplify 中的单独函数
series([x, x0, n, dir, logx, cdir])	在 x = x0 附近对 "self" 进行级数展开，当 n=None 时逐项给出级数项（即懒惰级数），否则当 n != None 时一次性给出所有项。
shift(s)	将函数平移一个与 x 无关的项。
shiftx(s)	将 x 按与 x 无关的项进行移位。
sigma_approximation([n])	返回相对于阶数 n 的傅里叶级数的 \(\sigma\)-近似。
simplify(**kwargs)	请参阅 sympy.simplify 中的 simplify 函数。
sort_key([order])
subs(*args, **kwargs)	在简化参数后，在表达式中用新内容替换旧内容。
taylor_term(n, x, *previous_terms)	泰勒项的一般方法。
term(pt)	系列中在点 pt 的项
together(*args, **kwargs)	请参阅 sympy.polys 中的 together 函数。
trigsimp(**args)	参见 sympy.simplify 中的 trigsimp 函数
truncate([n])	返回级数的前 n 个非零项。
xreplace(rule)	替换表达式中对象的出现。

伴随
as_base_exp
复制
差异
目录
is_hypergeometric
转置

参见

sympy.series.fourier.fourier_series

scale(s)

按一个与 x 无关的项缩放函数。

示例

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> s = fourier_series(x**2, (x, -pi, pi))
>>> s.scale(2).truncate()
-8*cos(x) + 2*cos(2*x) + 2*pi**2/3

scalex(s)

将 x 按与 x 无关的项进行缩放。

示例

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> s = fourier_series(x**2, (x, -pi, pi))
>>> s.scalex(2).truncate()
-4*cos(2*x) + cos(4*x) + pi**2/3

shift(s)

将函数平移一个与 x 无关的项。

示例

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> s = fourier_series(x**2, (x, -pi, pi))
>>> s.shift(1).truncate()
-4*cos(x) + cos(2*x) + 1 + pi**2/3

shiftx(s)

将 x 按与 x 无关的项进行移位。

示例

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> s = fourier_series(x**2, (x, -pi, pi))
>>> s.shiftx(1).truncate()
-4*cos(x + 1) + cos(2*x + 2) + pi**2/3

sigma_approximation(n=3)

返回相对于阶数 n 的傅里叶级数的 \(\sigma\)-近似。

参数:

n整数

近似中考虑的项的最高阶。

返回:

表达式

函数展开为傅里叶级数的Sigma近似。

参见

sympy.series.fourier.FourierSeries.truncate

注释

与 truncate() 不同，sigma_approximation() 的行为是不同的——它取所有小于 n 次幂的非零项，而不是前 n 个非零项。

参考文献

[1]

https://zh.wikipedia.org/wiki/%E5%90%89%E5%B8%83%E6%96%AF%E7%8E%B0%E8%B1%A1

[2]

https://en.wikipedia.org/wiki/Sigma_approximation

示例

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> s = fourier_series(x, (x, -pi, pi))
>>> s.sigma_approximation(4)
2*sin(x)*sinc(pi/4) - 2*sin(2*x)/pi + 2*sin(3*x)*sinc(3*pi/4)/3

truncate(n=3)

返回级数的前 n 个非零项。

如果 n 是 None，返回一个迭代器。

参数:

n整数或无

近似中非零项的数量，或为 None。

返回:

表达式或迭代器

将函数展开为傅里叶级数的近似。

参见

sympy.series.fourier.FourierSeries.sigma_approximation

示例

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> s = fourier_series(x, (x, -pi, pi))
>>> s.truncate(4)
2*sin(x) - sin(2*x) + 2*sin(3*x)/3 - sin(4*x)/2

sympy.series.fourier.fourier_series(f, limits=None, finite=True)

计算傅里叶三角级数展开。

参数:

限制（符号，开始，结束），可选

sym 表示计算级数所依据的符号。

start 和 end 表示傅里叶级数收敛到给定函数的区间的起点和终点。

默认范围指定为 \(-\pi\) 和 \(\pi\)。

返回:

傅里叶级数

表示傅里叶三角级数的符号对象。

参见

sympy.series.fourier.FourierSeries

注释

计算傅里叶级数可能会很慢，因为在计算 an, bn 时需要进行积分。

通过在已计算的傅里叶级数上使用移位和缩放来计算函数的傅里叶级数比重新计算要快。

例如，如果已知 x**2 的傅里叶级数，那么可以通过将 x**2 的傅里叶级数平移 -1 来找到 x**2 - 1 的傅里叶级数。

参考文献

[1]

https://mathworld.wolfram.com/FourierSeries.html

示例

计算 \(f(x) = x^2\) 的傅里叶级数：

>>> from sympy import fourier_series, pi
>>> from sympy.abc import x
>>> f = x**2
>>> s = fourier_series(f, (x, -pi, pi))
>>> s1 = s.truncate(n=3)
>>> s1
-4*cos(x) + cos(2*x) + pi**2/3

傅里叶级数的平移：

>>> s.shift(1).truncate()
-4*cos(x) + cos(2*x) + 1 + pi**2/3
>>> s.shiftx(1).truncate()
-4*cos(x + 1) + cos(2*x + 2) + pi**2/3

傅里叶级数的缩放：

>>> s.scale(2).truncate()
-8*cos(x) + 2*cos(2*x) + 2*pi**2/3
>>> s.scalex(2).truncate()
-4*cos(2*x) + cos(4*x) + pi**2/3

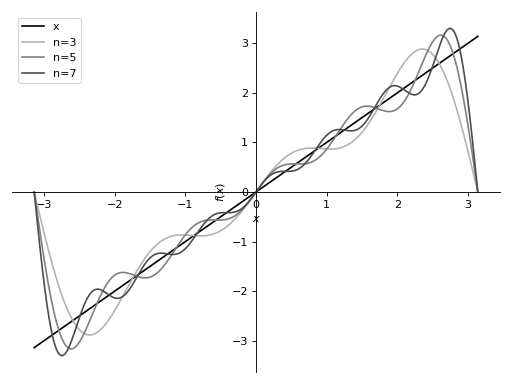
计算 \(f(x) = x\) 的傅里叶级数：

这说明了如何通过截断到更高阶来获得更好的收敛性。

>>> from sympy import fourier_series, pi, plot
>>> from sympy.abc import x
>>> f = x
>>> s = fourier_series(f, (x, -pi, pi))
>>> s1 = s.truncate(n = 3)
>>> s2 = s.truncate(n = 5)
>>> s3 = s.truncate(n = 7)
>>> p = plot(f, s1, s2, s3, (x, -pi, pi), show=False, legend=True)

>>> p[0].line_color = (0, 0, 0)
>>> p[0].label = 'x'
>>> p[1].line_color = (0.7, 0.7, 0.7)
>>> p[1].label = 'n=3'
>>> p[2].line_color = (0.5, 0.5, 0.5)
>>> p[2].label = 'n=5'
>>> p[3].line_color = (0.3, 0.3, 0.3)
>>> p[3].label = 'n=7'

>>> p.show()

(png, hires.png, pdf)

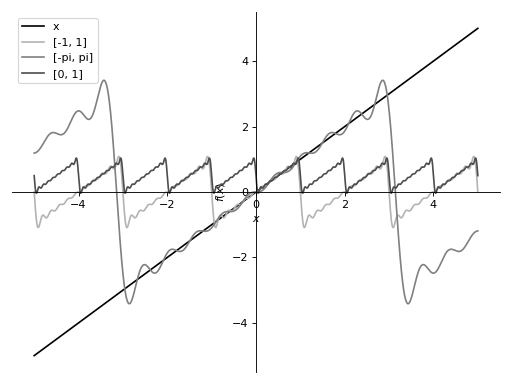
这说明了如果指定不同的范围，序列如何收敛到不同的锯齿波。

>>> s1 = fourier_series(x, (x, -1, 1)).truncate(10)
>>> s2 = fourier_series(x, (x, -pi, pi)).truncate(10)
>>> s3 = fourier_series(x, (x, 0, 1)).truncate(10)
>>> p = plot(x, s1, s2, s3, (x, -5, 5), show=False, legend=True)

>>> p[0].line_color = (0, 0, 0)
>>> p[0].label = 'x'
>>> p[1].line_color = (0.7, 0.7, 0.7)
>>> p[1].label = '[-1, 1]'
>>> p[2].line_color = (0.5, 0.5, 0.5)
>>> p[2].label = '[-pi, pi]'
>>> p[3].line_color = (0.3, 0.3, 0.3)
>>> p[3].label = '[0, 1]'

>>> p.show()

(png, hires.png, pdf)